電子學/運算放大器

電子學 | 前言 | 基礎電子學 | 複雜電子學 | 電學 | 機器 | 電子學史 | 附錄 | 編輯

運算放大器 (operational amplifier)

運算放大器，簡稱運放，是一種積體電路(IC)晶片。它是一個電子電路，包含許多電子元件，它們已經連線並封裝在晶片內部，並提供多個引腳用於外部連線。最初，運算放大器之所以得名，是因為它們被用於電子模擬計算機中，來模擬加法、減法、積分、微分等基本數學運算。從這個意義上說，真正的運算放大器是一個理想的電路元件。

運算放大器	引腳	符號

741 運算放大器

符號

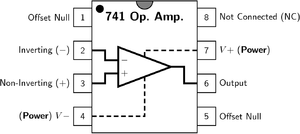
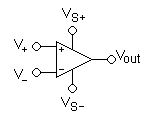
741 運算放大器具有如圖所示的符號。

其引腳為

V₊: 非反相輸入
V₋: 反相輸入
V_out: 輸出
V_S+: 正電源
V_S−: 負電源

運作

741 運算放大器可以被認為是通用電壓差放大器。741 運算放大器的主要功能是放大兩個輸入電壓的差值，可以用以下數學表示式表示

V_{o}=A(V_{+}-V_{-})

從

V_{o}=A(V_{+}-V_{-})

. 運算放大器起著電壓差放大器的作用。

可以證明，運算放大器可以作為非反相電壓放大器或反相電壓放大器。

V_{o}=AV_{+}

.

V_{-}=0

. 運算放大器作為非反相電壓放大器。

V_{o}=-AV_{-}

.

V_{+}=0

. 運算放大器作為反相電壓放大器。

此外，可以證明，運算放大器可以作為電壓比較器。

V_{o}=0

.

V_{-}=V_{+}

. 兩個輸入電壓之間沒有差異

V_o = V_S+ .

V_{+}>V_{-}

. 非反相輸入電壓大於反相輸入電壓

V_o = V_S- .

V_{-}>V_{+}

. 反相輸入電壓大於非反相輸入電壓。

理想運算放大器

輸出電壓是正負輸入之差乘以開環增益。

V_out = (V₊ − V₋) * A_vo.

理想運算放大器具有

無限開環增益，

無限輸入阻抗和

零輸出阻抗。

輸入阻抗是指非反相輸入和反相輸入之間的阻抗。

運算放大器的模型如圖 1 所示。其中 V₊ − V₋ 等於 v_d；R_in 是輸入阻抗；R_out 是輸出阻抗；A_vo 是開環增益；R_s 是源阻抗。

圖 1：運算放大器的模型。

使用分壓器規則，我們可以確定電壓 v_d。

v_{d}={\frac {V_{in}R_{in}}{R_{in}+R_{s}}}

(1)

由於受控電壓源將電壓 v_d 放大 A_vo 倍。我們再次使用分壓器規則可以算出 R_L 兩端的輸出電壓。

V_{out}={\frac {A_{vo}v_{d}R_{L}}{R_{L}+R_{out}}}

(2)

將公式 1 代入公式 2。

V_{out}={\frac {A_{vo}V_{in}R_{in}R_{L}}{(R_{L}+R_{out})(R_{in}+R_{s})}}

現在如果應用理想運算放大器的特性。理想運算放大器的特性是無限的輸入阻抗和零輸出阻抗。由於 R_in >>，遠大於 R_s，R_in/(R_in+R_s) $\approx$ 1。

V_{out}=A_{vo}V_{in}\,

這基本上是運算放大器的定義。但是如果輸入阻抗不是無限的，輸出阻抗也不是零，那麼就不是這樣。

實際運算放大器

實際運算放大器通常是以積體電路的形式製造的，但有時也使用分立電晶體或真空管。實際運算放大器是理想運算放大器的近似值。實際運算放大器沒有無限的開環增益、無限的輸入阻抗或零輸出阻抗。實際運算放大器還會在電路中產生噪聲，並具有偏移電壓、熱漂移和有限頻寬。

偏移電壓

意味著當兩個輸入都接地時，存在一個電壓 v_d。這種偏移稱為輸入偏移，因為電壓 v_d 偏離了其理想值零伏。輸入偏移電壓乘以開環增益，得到輸出偏移電壓。

熱漂移

意味著運算放大器的特性隨溫度變化而變化。也就是說，開環增益、輸入和輸出阻抗、偏移電壓和頻寬都會隨著溫度的變化而變化。

有限頻寬

運算放大器是由電晶體組成的。電晶體由於其自身的某些電容，只能以一定速率響應。這意味著運算放大器無法對高於一定水平的頻率做出足夠快的響應。這個水平就是頻寬。

現代積體電路 MOSFET 運算放大器在有限頻寬、大訊號應用中，在室溫下越來越接近這些理想值。當近似值足夠接近時，我們就可以繼續將實際器件稱為“運算放大器”，忽略其限制，並使用本文中給出的思想和公式。

直流特性

開環增益定義為從輸入到輸出的放大倍數，沒有任何反饋。在大多數實際計算中，開環增益被認為是無限的；然而在現實中，它受限於為運算放大器供電的電壓量，即上圖中的 Vs+ 和 Vs-。典型器件的開環直流增益在 100,000 到 100 萬以上之間。這使得使用負反饋可以輕鬆、準確地設定應用中的增益。當然，理論和實踐會有所不同，因為運算放大器存在設計者必須牢記並有時需要克服的限制。

交流特性

在直流條件下計算的運算放大器增益在較高頻率下不適用。這種現象是由於運算放大器本身的限制（如有限頻寬）以及運算放大器所處電路的交流特性造成的。在使用運算放大器進行設計時，最著名的障礙是器件在高頻下發生諧振的趨勢，因為寄生低通濾波器會使負反饋變為正反饋。

典型的低成本通用運算放大器的增益頻寬積為幾兆赫茲。專用高速運算放大器的增益頻寬積可以達到幾百兆赫茲。

運算放大器配置

應用

快速設計流程

假設我們有一個（弱）輸入訊號，我們想放大它以產生一個強大的輸出訊號；或者我們有幾個不同的電壓，我們想將它們加在一起。為了實現這些目的，我們需要運算放大器放大和求和電路。這些基本的（通常是單運算放大器）電路似乎沒有新東西可以說了。只是創新者 Dieter Knollman 在一篇 EDN 文章 ^[1] 中提出了一種新的更簡單的設計方法。他還將他的工作釋出在網上^[2]（參見在 Dieter 工作之後寫的一篇電路故事^[3]）。

我們假設

所有輸入都是理想電壓源。
增益定義為從理想電壓源到運算放大器輸出的增益。
反饋電阻 Rf 連線從運算放大器輸出到反相輸入。
輸入電阻 Ri 連線從理想電壓源輸入到運算放大器輸入。（這 *包含* 任何源電阻）。
- 正增益輸入透過該電阻連線到 V₊
- 負增益輸入透過該電阻連線到 V₋

設計步驟

首先，指定每個輸入所需的電路增益。
然後計算地增益，如下所示

黛西定理

在一個設計合理的運算放大器電路中，增益之和 = +1。

因此，選擇

地增益 = 1 - (所需的正增益和負增益之和).

選擇一個反饋電阻值。例如，設 Rf=100 千歐。

接下來，使用以下公式計算每個輸入的電阻值，包括地增益電阻。

Ri={\frac {Rf}{|gain|}}

.

其中 |gain| 是所需增益的絕對值。

一些運算放大器電路需要從運算放大器的反相輸入到地連線一個電阻。其他電路需要在同相輸入上連線一個到地的電阻。地增益的符號決定了將地電阻放置在何處。

如果所需的增益之和為 1，則無需連線到地的電阻。

您將在下面看到一些示例，說明如何使用快速設計步驟。首先，回答這個問題，“您希望輸出電壓的最高和最低值是多少？”確保運算放大器的電源端至少達到這些最高和最低值。（如果您希望它從 +5 V 擺動到 -5 V，那麼連線到 0 V 和 +10 V 的運算放大器將無法工作）。

通用運算放大器有兩個輸入和一個輸出。（有些是用浮動、差分輸出製作的。）輸出電壓是兩個輸入之差的倍數。

浮動輸出？您可能誤解了“全差分放大器” ？

V_out = G(V₊ − V₋)

G 是運算放大器的開環增益。假定輸入具有非常高的阻抗；輸入不會流入或流出明顯的電流。運算放大器輸出具有非常低的源阻抗。

如果運算放大器與正反饋一起使用，它可以充當振盪器。

其他符號

電源引腳（V_S+ 和 V_S−）可以用多種不同的方式標記。對於基於 FET 的運算放大器，正極公共漏極電源標記為 V_DD，負極公共源極電源標記為 V_SS。對於基於 BJT 的運算放大器，V_S+ 引腳變為 V_CC，V_S− 變為 V_EE。它們有時也標記為 V_CC+ 和 V_CC−，甚至 V₊ 和 V₋，在這種情況下，輸入將被不同地標記。功能保持不變。