零多項式  每個數都是P的根。這是唯一具有無限多個根的多項式。一個非零多項式具有一定的次數n(n可以是0、1、2,…),並且不能超過n個根,因為根據代數的一個著名定理,如果
每個數都是P的根。這是唯一具有無限多個根的多項式。一個非零多項式具有一定的次數n(n可以是0、1、2,…),並且不能超過n個根,因為根據代數的一個著名定理,如果  (對於成對不同的
(對於成對不同的  ),那麼必然
),那麼必然  對於一些非零多項式Q,次數為
對於一些非零多項式Q,次數為 
每個具有整數係數的多項式P都是整值,即它的值P(k)對於每個整數k都是整數;但反過來只有對於一次多項式(線性函式)才成立。例如,多項式  每當x是整數時,都會取整數值。這是因為x和x-1中一定有一個是偶數。值
每當x是整數時,都會取整數值。這是因為x和x-1中一定有一個是偶數。值  是二項式係數。
是二項式係數。
更一般地,對於每個n=0、1、2、3,…,多項式  是整值;
是整值;  是二項式係數。事實上,每個整值多項式都是這些Pn的整數線性組合。
是二項式係數。事實上,每個整值多項式都是這些Pn的整數線性組合。
 餘弦:顯著值
餘弦:顯著值
餘弦函式, 滿足
滿足 



 同時
同時  以及
以及  對於所有 x 成立,這為
對於所有 x 成立,這為  是以下數字之一提供了無限個 x:
是以下數字之一提供了無限個 x: 也就是說,圖上有無限多個點。多項式無法滿足所有這些條件,因為
也就是說,圖上有無限多個點。多項式無法滿足所有這些條件,因為  當
當  對於每個非恆定多項式 P 成立;它可以滿足其中一部分嗎?
對於每個非恆定多項式 P 成立;它可以滿足其中一部分嗎?
我們嘗試尋找滿足五個條件的P



 為了方便,我們對x進行重新縮放,令
為了方便,我們對x進行重新縮放,令 ,並將五個條件改寫成Q的形式:
,並將五個條件改寫成Q的形式:



 為了找到這樣的Q,我們使用拉格朗日多項式。
為了找到這樣的Q,我們使用拉格朗日多項式。
 拉格朗日插值多項式
拉格朗日插值多項式
使用五次多項式  ,它在給定點 0, 2, 3, 4, 6 處有根,並考慮到
,它在給定點 0, 2, 3, 4, 6 處有根,並考慮到  (透過對乘積進行微分來驗證),我們考慮所謂的拉格朗日基多項式
(透過對乘積進行微分來驗證),我們考慮所謂的拉格朗日基多項式  ,它在 2, 3, 4, 6 處有根(但不在 0 處);左手邊的除法被解釋為多項式的代數除法(即,找到一個多項式,它與分母的乘積是分子
,它在 2, 3, 4, 6 處有根(但不在 0 處);左手邊的除法被解釋為多項式的代數除法(即,找到一個多項式,它與分母的乘積是分子  )而不是函式的除法,因此商對於所有x都定義,包括 0。它在 0 處的值為 1。思考一下為什麼;看圖;回憶一下
)而不是函式的除法,因此商對於所有x都定義,包括 0。它在 0 處的值為 1。思考一下為什麼;看圖;回憶一下  。
。
類似地,第二個拉格朗日基多項式  分別在 0, 2, 3, 4, 6 處取值 0, 1, 0, 0, 0。第三個
分別在 0, 2, 3, 4, 6 處取值 0, 1, 0, 0, 0。第三個  分別取值 0, 0, 1, 0, 0。依此類推(計算第四個和第五個)。現在,只需將這五個拉格朗日基多項式與係數(等於Q的所需值)相結合即可。
分別取值 0, 0, 1, 0, 0。依此類推(計算第四個和第五個)。現在,只需將這五個拉格朗日基多項式與係數(等於Q的所需值)相結合即可。

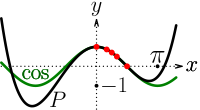 餘弦函式的多項式逼近
餘弦函式的多項式逼近
最後, 正如我們從圖中看到的那樣,這兩個函式在
正如我們從圖中看到的那樣,這兩個函式在  範圍內非常接近;實際上,對於這些 x,
範圍內非常接近;實際上,對於這些 x,  的最大值約為 0.00029。
的最大值約為 0.00029。
可以透過導數得到更好的近似值。函式 的導數為
的導數為  因此有
因此有 



 相應的導數
相應的導數  接近但不同;例如,
接近但不同;例如,

為了修正導數而不破壞數值,我們將  替換為
替換為  ,其中
,其中  是一個 4 次多項式,使得
是一個 4 次多項式,使得  的導數等於
的導數等於  ,其中
,其中  也就是說,
也就是說, 因為對於這些 x,
因為對於這些 x, ;所以,
;所以,
 ,其中
,其中 
我們像以前一樣找到這樣的 R

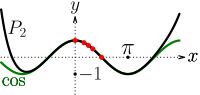 餘弦函式的多項式逼近
餘弦函式的多項式逼近
並得到更好的逼近  事實上,
事實上, 如果你仍然想要更小的誤差,嘗試二階導數和
如果你仍然想要更小的誤差,嘗試二階導數和 
餘弦函式, 滿足
滿足  並且有無窮多個根:
並且有無窮多個根: 多項式不能滿足所有這些條件;它能滿足其中有限部分嗎?
多項式不能滿足所有這些條件;它能滿足其中有限部分嗎?
很容易找到一個多項式P,使得 並且
並且  即
即  (驗證一下)。那麼
(驗證一下)。那麼  並且
並且 
由於條件對x的符號不敏感,我們尋找一個 的多項式,也就是說,
的多項式,也就是說, ,其中Q滿足
,其中Q滿足  以及
以及  很容易找到這樣的Q,即
很容易找到這樣的Q,即  (驗證一下),這導致了
(驗證一下),這導致了
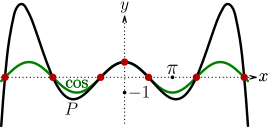
 餘弦函式的多項式逼近
餘弦函式的多項式逼近
 就像我們在圖中看到的,這兩個函式在
就像我們在圖中看到的,這兩個函式在 範圍內非常接近;事實上,對於這些x,
範圍內非常接近;事實上,對於這些x, 的最大值約為 0.028,而
的最大值約為 0.028,而 (對於這些x)約為 0.056。
(對於這些x)約為 0.056。
 餘弦函式的多項式逼近
餘弦函式的多項式逼近
在這個方向上的下一步是:


等等。對於每個 ,多項式
,多項式

滿足 和
和  這很容易驗證。更難(但可能)證明
這很容易驗證。更難(但可能)證明  作為
作為  它將餘弦表示為無限乘積
它將餘弦表示為無限乘積

 餘弦函式的多項式逼近
餘弦函式的多項式逼近
另一方面,眾所周知的冪級數  給出了另一個多項式序列
給出了另一個多項式序列  收斂到相同的餘弦函式。見圖中的 Q3;
收斂到相同的餘弦函式。見圖中的 Q3;
我們可以透過展開括號來檢查等式 的正確性嗎?讓我們試一下。常數項係數:1=1。x2 的係數:
的正確性嗎?讓我們試一下。常數項係數:1=1。x2 的係數: 也就是說,
也就是說, 真的嗎?是的,
真的嗎?是的, 著名的平方倒數級數起著重要作用。
著名的平方倒數級數起著重要作用。
這種非嚴格的括號展開可以嚴格地表示如下。對於任何多項式 *P*,常數項是 *P* 在零點的值,即 *P*(0);*x* 的係數是導數 *P* '(0) 在零點的值;*x*2 的係數是二階導數 *P''*(0) 在零點的值的一半,即 ½*P''*(0)。顯然,
 和
和  對於所有
對於所有  (如前所述,
(如前所述, )。上面的計算表明
)。上面的計算表明  當 *n* 趨於無窮大時。那麼,更高階導數,
當 *n* 趨於無窮大時。那麼,更高階導數, 是否收斂於
是否收斂於  ?將上面的計算推廣到 *k*=4、6……是乏味的(甚至可能無法實現);幸運的是,有一個更好的方法。也就是說,
?將上面的計算推廣到 *k*=4、6……是乏味的(甚至可能無法實現);幸運的是,有一個更好的方法。也就是說, 對於所有複數 *z*,而且,
對於所有複數 *z*,而且, 對於每個 *R*>0。利用柯西微分公式,我們可以得出結論,
對於每個 *R*>0。利用柯西微分公式,我們可以得出結論, (當
(當  )對於每個 *k*,特別是,
)對於每個 *k*,特別是,

當  時,我們有
時,我們有  (思考一下,為什麼)當
(思考一下,為什麼)當  然而,零點的導數並不收斂到 0;相反,它等於 1(對於所有 *n*),因為,表示
然而,零點的導數並不收斂到 0;相反,它等於 1(對於所有 *n*),因為,表示  我們有
我們有 

 極限的導數
極限的導數
因此,函式序列  在區間
在區間 ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) 上的極限是零函式,因此極限的導數也是零函式。然而,導數序列
上的極限是零函式,因此極限的導數也是零函式。然而,導數序列  至少在
至少在  處不為零。對於
處不為零。對於  情況如何?這裡導數的極限為零,因為
情況如何?這裡導數的極限為零,因為  (檢查一下;第二個因子的指數衰減超過了第一個因子的線性增長)。因此,
(檢查一下;第二個因子的指數衰減超過了第一個因子的線性增長)。因此,

導數和極限並不總是可以交換的。
請注意,函式 *f* 有兩個等效定義;一個是分段的(對於某些 *x*,一個值,對於其他 *x*,另一個值,等等),但另一個是單個表示式  ,對於所有這些 *x*。
,對於所有這些 *x*。
函式 *f* 在 (0) 處不連續,儘管它是連續函式  的極限。這在逐點收斂的情況下可能發生(即,在所考慮域的每個點都收斂),因為收斂速度可能取決於該點。
的極限。這在逐點收斂的情況下可能發生(即,在所考慮域的每個點都收斂),因為收斂速度可能取決於該點。
否則(當收斂速度不依賴於該點時),收斂稱為一致收斂;根據一致收斂定理,連續函式的一致極限是一個連續函式。
由此可知, (到 *f*)的收斂是非一致的,但這只是一個反證法。
(到 *f*)的收斂是非一致的,但這只是一個反證法。
從直接證明可以更好地理解這一點。導數  無法一致收斂,因為
無法一致收斂,因為  無法變得很小(當 *n* 很大時)對於某些靠近 0 的 *x*;例如,試試
無法變得很小(當 *n* 很大時)對於某些靠近 0 的 *x*;例如,試試 

對於所有 並且
並且 不為零(除非
不為零(除非 )。
)。
相反, 在
在![{\displaystyle [-1,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9c504e0d448149f190679df28cd10275a67f117) 上一致收斂,也就是說,
上一致收斂,也就是說, 隨著
隨著 ,因為最大值出現在
,因為最大值出現在 (透過解方程
(透過解方程 進行驗證) 並且
進行驗證) 並且 然而,交換導數和極限運算似乎是不可能的。將此情況與一個眾所周知的定理進行比較
然而,交換導數和極限運算似乎是不可能的。將此情況與一個眾所周知的定理進行比較
- 如果
 是
是 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上的可微函式序列,使得
上的可微函式序列,使得  存在(且有限)對於某些
存在(且有限)對於某些 ![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145) ,並且序列
,並且序列  在
在 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上一致收斂,那麼
上一致收斂,那麼  在
在 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上一致收斂於函式
上一致收斂於函式  ,並且
,並且  對於
對於 ![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) 成立。
成立。
導數  的一致收斂是必需的;函式
的一致收斂是必需的;函式  的一致收斂是不夠的。
的一致收斂是不夠的。
複數在 第 “多項式模擬餘弦:根” 節 中很有用,但在這裡無能為力,因為對於  ,我們有
,我們有  對於所有
對於所有 
每個人都知道如何透過座標平面上的曲線來視覺化連續函式的行為。為此,人們對函式圖形上的足夠多的點  進行取樣,將它們繪製在
進行取樣,將它們繪製在  平面上,然後用曲線連線這些點,繪製出圖形。然而,這個看似毫無爭議的想法卻被一些奇特的函式所挑戰,這些函式有時被稱為“連續怪物”。它們通常是所謂的間隙三角級數的和
平面上,然後用曲線連線這些點,繪製出圖形。然而,這個看似毫無爭議的想法卻被一些奇特的函式所挑戰,這些函式有時被稱為“連續怪物”。它們通常是所謂的間隙三角級數的和
 (其中數字
(其中數字  相距很遠)。
相距很遠)。
其中最著名的就是魏爾斯特拉斯函式
 (對於適當的
(對於適當的  使得
使得  )。
)。
根據 Jarnicki 和 Pflug(第 3.1 節),這是  (類似的正弦函式級數是
(類似的正弦函式級數是  )。
)。
 魏爾斯特拉斯函式
魏爾斯特拉斯函式
這幅影像(由邁克爾·麥克勞克林根據上述維基百科文章在此處複製,以及由理查德·利普頓在此處複製,但沒有參考)實際上是函式 的近似
的近似 的圖形,透過連線
的圖形,透過連線 個取樣點(可以透過檢查XML 程式碼,該程式碼位於SVG 檔案中)獲得。雖然看起來像一條曲線,但它顯得相當奇怪。最後兩個求和項被扭曲了,因為步長
個取樣點(可以透過檢查XML 程式碼,該程式碼位於SVG 檔案中)獲得。雖然看起來像一條曲線,但它顯得相當奇怪。最後兩個求和項被扭曲了,因為步長 超過了
超過了 的週期
的週期 ,並且接近
,並且接近 的一半週期
的一半週期 。然而,所有
。然而,所有 的項最多貢獻
的項最多貢獻 也就是說,對於所有的
也就是說,對於所有的 ,
, ;除非放大影像,否則這種差異幾乎不可見。
;除非放大影像,否則這種差異幾乎不可見。
到目前為止,一切順利。但這個怪物還不是最糟糕的。為了得到一個更可怕的間斷三角級數,人們可以嘗試頻率  比
比  增加得更快,或者係數比
增加得更快,或者係數比  減少得更慢,或者兩者兼而有之。
減少得更慢,或者兩者兼而有之。
讓我們嘗試一下這個級數

這些係數  很方便,因為它們的和是(有限的且)明顯的:
很方便,因為它們的和是(有限的且)明顯的: 因此,
因此, (因為
(因為  ),以及
),以及  對所有
對所有  (因為
(因為  )。
)。
類似地, 以及
以及  因此,部分和
因此,部分和 和尾部
和尾部  滿足
滿足
 以及
以及 
 對所有
對所有 
由於明顯的對稱性(見 在週期
在週期![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) 上的圖形),只需要在
上的圖形),只需要在![{\displaystyle [0,\,1/4].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a3779c656673995bc801d2b58de24cf558d91c) 上繪製此函式。
上繪製此函式。
 部分和
部分和 ,放大4倍
,放大4倍
仔細觀察 的圖形,我們開始產生懷疑。乍一看,它是用較粗的筆繪製的。但事實並非如此;一些(幾乎?)垂直線很細。所以,我們在這裡看到的是一條曲線,還是兩條“平行”曲線之間的區域?
的圖形,我們開始產生懷疑。乍一看,它是用較粗的筆繪製的。但事實並非如此;一些(幾乎?)垂直線很細。所以,我們在這裡看到的是一條曲線,還是兩條“平行”曲線之間的區域?
 和
和  ,放大40倍
,放大40倍 和
和  ,放大400倍
,放大400倍 的圖形在放大後變得清晰可見,但隨著
的圖形在放大後變得清晰可見,但隨著  的出現,這種懷疑又回來了,而且更加強烈。再放大一次只會讓情況更糟。我們意識到,
的出現,這種懷疑又回來了,而且更加強烈。再放大一次只會讓情況更糟。我們意識到, 在
在 ![{\displaystyle [0,\,1/4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9004d2adb92cccf16fa579e9f9c5ee33436ea21) 上的圖形看起來過於完美。特別是,
上的圖形看起來過於完美。特別是, 的圖形似乎穿過了紅色框的上側。那麼,如何才能更接近
的圖形似乎穿過了紅色框的上側。那麼,如何才能更接近  的圖形呢?
的圖形呢?
幸運的是,對於  的某些特殊值,
的某些特殊值, 的確切值是顯而易見的。首先,
的確切值是顯而易見的。首先, (見上文),因此對於所有整數
(見上文),因此對於所有整數  ,都有
,都有  ,這是由於週期性:對於所有
,這是由於週期性:對於所有  都有
都有  。類似地,
。類似地, 因為對於所有奇數整數
因為對於所有奇數整數  ,都有
,都有  (特別是,
(特別是, )。另一方面,對於所有
)。另一方面,對於所有  ,都有
,都有  。
。
去掉第一個加數,我們得到第一個尾部  ,週期為
,週期為  因此,
因此, 並且
並且  對所有整數
對所有整數  另一方面,
另一方面, 對所有
對所有  因此,
因此,
透過 
透過 

 對於所有整數
對於所有整數 
 對於所有
對於所有 
類似地,對於所有 

 對於所有整數
對於所有整數 
 對所有
對所有 
 透過
透過  放大 400 倍;同樣是
放大 400 倍;同樣是 
回到  和
和  在
在 ![{\displaystyle [0.11,0.1125],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fab191a2ce96cea580ffa280faca3027caec0f2a) 上,我們透過
上,我們透過  新增特殊值和邊界,可以發現
新增特殊值和邊界,可以發現  比
比  距離
距離  更遠,而
更遠,而  距離
距離  在紅色曲線上我們有超過 440 個點,藍色曲線上也有同樣多的點。
在紅色曲線上我們有超過 440 個點,藍色曲線上也有同樣多的點。

 的圖形,放大 400 倍。
的圖形,放大 400 倍。
因此,如果圖片的橫向尺寸小於 440 畫素,那麼  的圖形不可避免地會穿過紅色曲線和藍色曲線之間的所有畫素!在給定的解析度下,
的圖形不可避免地會穿過紅色曲線和藍色曲線之間的所有畫素!在給定的解析度下, 的圖形看起來不像一條曲線,而像是兩條平行曲線之間的區域。
的圖形看起來不像一條曲線,而像是兩條平行曲線之間的區域。
這本身並不令人驚訝。例如,一個由 100 赫茲聲音調製的 10 兆赫茲無線電波可以用以下函式來描述: 例如,在
例如,在 ![{\displaystyle [0,0.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b836c8608550b3f9099d9139d54844c3ff2ac90) 上,
上, 的圖形看起來不像一條曲線,而是兩條曲線之間的區域,即
的圖形看起來不像一條曲線,而是兩條曲線之間的區域,即  並在
並在 ![{\displaystyle [0,10^{-4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87833759ab933d5aa5219a2218195a9feb83f34f) 上看起來像一個矩形區域。然而,放大最終會有所幫助;在
上看起來像一個矩形區域。然而,放大最終會有所幫助;在 ![{\displaystyle [0,10^{-6}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfcc09a07655df351485915d402798ea050c908d) (或任何其他 1 微秒間隔)上,
(或任何其他 1 微秒間隔)上, 的圖形看起來像一條曲線。
的圖形看起來像一條曲線。
相比之下,對於  ,放大永遠不會有幫助,只會讓情況變得更糟。實際上,最終會導致圖形看起來像一個矩形區域。這顯示了
,放大永遠不會有幫助,只會讓情況變得更糟。實際上,最終會導致圖形看起來像一個矩形區域。這顯示了  的巨大性質。另一方面,當放大趨於無窮大時,(近似)矩形區域的高度收斂於零;這顯示了
的巨大性質。另一方面,當放大趨於無窮大時,(近似)矩形區域的高度收斂於零;這顯示了  的連續性質。
的連續性質。

 圖形的隨機樣本點。
圖形的隨機樣本點。
用類似區域圖的圖形進行視覺化效果並不理想。雖然無法繪製曲線圖,但我們仍然可以做得更多。我們可以隨機選擇許多 的值,計算給定函式對應的
的值,計算給定函式對應的 值,並繪製點
值,並繪製點 這張圖顯示了
這張圖顯示了 個隨機點在尾部
個隨機點在尾部 圖形上的樣本,這些樣本位於該尾部週期(由於明顯的對稱性,如前所述,第一個週期就足夠了)的第一象限。事實上,這裡使用函式
圖形上的樣本,這些樣本位於該尾部週期(由於明顯的對稱性,如前所述,第一個週期就足夠了)的第一象限。事實上,這裡使用函式 作為
作為 的一個令人滿意的近似,每個
的一個令人滿意的近似,每個 都用超過
都用超過 位三進位制(即以 3 為底)數字來指定,以便計算
位三進位制(即以 3 為底)數字來指定,以便計算
和以前一樣,紅線和藍線是給定函式 (透過
(透過 )的邊界,而這些曲線上的點是特殊值。令人驚訝的是:所有
)的邊界,而這些曲線上的點是特殊值。令人驚訝的是:所有 個隨機點都遠離這些邊界!通常
個隨機點都遠離這些邊界!通常 個點就足以獲得函式最大值的滿意圖片。但對於這個怪物,
個點就足以獲得函式最大值的滿意圖片。但對於這個怪物, 個點太少了。
個點太少了。
通常,對於間斷三角級數的和,即使是近似地,例如,相對誤差小於 10%,也很難找到它的最大值和最小值(在給定區間內)。我們選擇頻率  與我們使用餘弦而不是正弦相一致,使我們能夠找到和的異常高值。為了充分理解這種好運,試著最大化如下函式
與我們使用餘弦而不是正弦相一致,使我們能夠找到和的異常高值。為了充分理解這種好運,試著最大化如下函式  或最小化
或最小化  ,你會意識到為什麼魏爾斯特拉斯更喜歡餘弦函式和形式為
,你會意識到為什麼魏爾斯特拉斯更喜歡餘弦函式和形式為  的頻率,其中
的頻率,其中  是一個正奇數。常用的數值最佳化方法失效,因為區域性極值點很多且非常尖銳。由於連續性,怪獸函式在其最大化點的某個鄰域內接近其最大值,但這個鄰域非常小;隨機點幾乎沒有機會進入這樣的鄰域。絕大多數值遠非極值。
是一個正奇數。常用的數值最佳化方法失效,因為區域性極值點很多且非常尖銳。由於連續性,怪獸函式在其最大化點的某個鄰域內接近其最大值,但這個鄰域非常小;隨機點幾乎沒有機會進入這樣的鄰域。絕大多數值遠非極值。

 影像上樣本點的遞增重排。
影像上樣本點的遞增重排。
為了研究尾部  在其週期上的值分佈,可以取
在其週期上的值分佈,可以取  個值
個值  在週期的第一個象限(上面使用),以及
在週期的第一個象限(上面使用),以及  個相反數
個相反數  (這些是第二象限的值),將所有這些
(這些是第二象限的值),將所有這些  個數字按升序排序,並將結果視為新函式在等間距點上的值。這是結果的繪圖,參見紅色曲線。這是對所謂的給定函式的單調(遞增)重排的數值近似。
個數字按升序排序,並將結果視為新函式在等間距點上的值。這是結果的繪圖,參見紅色曲線。這是對所謂的給定函式的單調(遞增)重排的數值近似。
值得注意的是,結果非常接近著名的正態分佈  ,紅色曲線非常接近相應的分位數函式
,紅色曲線非常接近相應的分位數函式  (由黑點表示)。
(由黑點表示)。
(這裡  ) 奇妙的是,該函式本身很複雜,但其單調重排卻很簡潔。為什麼會出現這種情況?
) 奇妙的是,該函式本身很複雜,但其單調重排卻很簡潔。為什麼會出現這種情況?
給定的函式是由許多項(形式為  ) 構成;而 *“中心極限定理指出,在一定(相當普遍的)條件下,許多隨機變數的和將近似服從正態分佈。”*
) 構成;而 *“中心極限定理指出,在一定(相當普遍的)條件下,許多隨機變數的和將近似服從正態分佈。”*
從均勻分佈中隨機選取一個點 ![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2) ,我們可以將這些項視為隨機變數。但是,條件之一是獨立性;而我們的這些項是相關的,而且是函式相關的,因為
,我們可以將這些項視為隨機變數。但是,條件之一是獨立性;而我們的這些項是相關的,而且是函式相關的,因為  (更一般地說,
(更一般地說, 
 是 切比雪夫多項式。)然而,對間斷三角級數的機率方法仍然存在,並能帶來成果;特別是,正態分佈在這種情況下出現是一個眾所周知的現象。
是 切比雪夫多項式。)然而,對間斷三角級數的機率方法仍然存在,並能帶來成果;特別是,正態分佈在這種情況下出現是一個眾所周知的現象。
但顯然,正態逼近在某個地方必須失效,因為我們的函式是有界的(以  為界),而正態隨機變數不是。
為界),而正態隨機變數不是。
中心極限定理名稱中的“中心”有兩種解釋:(1)在機率論中具有核心重要性;(2)描述分佈的中心,而不是其尾部,也就是說,描述的是大偏差。

 的遞增重排,縮放比例為 40。
的遞增重排,縮放比例為 40。
在正態分佈中,高於  的偏差出現的機率為
的偏差出現的機率為  因此,對於
因此,對於  不等式
不等式  在總長度為
在總長度為  的區間上成立,大小為
的區間上成立,大小為  的隨機樣本應該包含大約
的隨機樣本應該包含大約  個這樣的值。這在前面的圖片中是看不出來的,但在放大的圖片中就很明顯了。
個這樣的值。這在前面的圖片中是看不出來的,但在放大的圖片中就很明顯了。
 對
對  進行遞增重排,對數刻度。
進行遞增重排,對數刻度。
對於 ,正態機率僅為
,正態機率僅為 且
且 僅為
僅為  為了觀察
為了觀察  和
和  情況,我們需要更大的樣本量和對數刻度。這最後一張圖片展示了一個大小為
情況,我們需要更大的樣本量和對數刻度。這最後一張圖片展示了一個大小為 的樣本(這需要計算機幾個小時來完成)。我們看到,分佈在
的樣本(這需要計算機幾個小時來完成)。我們看到,分佈在  附近接近正態分佈,但在
附近接近正態分佈,但在  偏離正態分佈。希望,近似正態性遵循一些適用於
偏離正態分佈。希望,近似正態性遵循一些適用於  的中等偏差理論,而偏離正態性遵循一些適用於
的中等偏差理論,而偏離正態性遵循一些適用於  及更遠位置的大偏差理論;但目前,儘管在間隙級數的機率方法方面取得了進展,但這樣的理論還沒有出現,圖片中大紅色問號附近的情況仍然未知。自然可以猜測,在這個區域,
及更遠位置的大偏差理論;但目前,儘管在間隙級數的機率方法方面取得了進展,但這樣的理論還沒有出現,圖片中大紅色問號附近的情況仍然未知。自然可以猜測,在這個區域, 偏差的機率小於其正態近似值,因此,小於
偏差的機率小於其正態近似值,因此,小於 
假設這個猜想是正確的,並考慮到  且
且  我們得出結論,函式
我們得出結論,函式  超過其最大值的
超過其最大值的  ,在總長度小於(可能遠小於)
,在總長度小於(可能遠小於) 的區間上。
的區間上。
但是,同樣,這個怪物並不是最糟糕的。為了得到一個更加可怕的缺失三角級數,人們可以嘗試頻率  比
比  增加得更快,或者係數比
增加得更快,或者係數比  減少得更慢,或者兩者兼而有之。出乎意料的是,或者說並不那麼出乎意料的是,這些函式在分析上越可怕,在機率上就越容易處理。(在 Delbaen 和 Hovhannisyan 的論文中,請注意係數
減少得更慢,或者兩者兼而有之。出乎意料的是,或者說並不那麼出乎意料的是,這些函式在分析上越可怕,在機率上就越容易處理。(在 Delbaen 和 Hovhannisyan 的論文中,請注意係數  對於
對於  在備註 2.3 中;也請注意“大間隙”定理 1.4、2.15、2.16 對於
在備註 2.3 中;也請注意“大間隙”定理 1.4、2.15、2.16 對於  )。這是由 德布魯因 提出的一般現象的特殊情況,如下所示。
)。這是由 德布魯因 提出的一般現象的特殊情況,如下所示。
- 我們經常需要評估某個數字 [...] 使得直接方法幾乎是不可行的 [...] 我們應該非常高興擁有一個完全不同的方法 [...] 至少可以提供一些有用的資訊。通常,這種新方法給出的結果(正如 拉普拉斯 所指出的)與其必要程度成正比。 [...]
- N.G. 德布魯因,分析中的漸近方法,北荷蘭出版社,1958 年。參見第 1.1 節“什麼是漸近線?”(第 1 頁)。
 多項式 在維基百科。
多項式 在維基百科。 整值多項式 在維基百科。
整值多項式 在維基百科。 二項式係數 在維基百科。
二項式係數 在維基百科。






 平方倒數級數 在維基百科。
平方倒數級數 在維基百科。
 分段函式 在維基百科。
分段函式 在維基百科。 逐點收斂 在維基百科。
逐點收斂 在維基百科。 一致收斂#到連續性 在維基百科。
一致收斂#到連續性 在維基百科。 反證法 在維基百科。
反證法 在維基百科。 維基百科上的間隙函式#間隙三角級數。 (也在 EoM 上的間隙三角級數)。
維基百科上的間隙函式#間隙三角級數。 (也在 EoM 上的間隙三角級數)。





 正態分佈 在維基百科。
正態分佈 在維基百科。 正態分佈#分位數函式 在維基百科。
正態分佈#分位數函式 在維基百科。 正態分佈#中心極限定理 在維基百科。
正態分佈#中心極限定理 在維基百科。 中心極限定理#間斷三角級數 在維基百科。
中心極限定理#間斷三角級數 在維基百科。
 中心極限定理#歷史 在維基百科上。
中心極限定理#歷史 在維基百科上。 大偏差理論 在維基百科上。
大偏差理論 在維基百科上。























































































































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)















![{\displaystyle [-1,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9c504e0d448149f190679df28cd10275a67f117)





![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)




![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)




















































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle [0,\,1/4].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a3779c656673995bc801d2b58de24cf558d91c)









![{\displaystyle [0,\,1/4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9004d2adb92cccf16fa579e9f9c5ee33436ea21)





























![{\displaystyle [0.11,0.1125],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fab191a2ce96cea580ffa280faca3027caec0f2a)



![{\displaystyle [0,0.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b836c8608550b3f9099d9139d54844c3ff2ac90)


![{\displaystyle [0,10^{-4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87833759ab933d5aa5219a2218195a9feb83f34f)
![{\displaystyle [0,10^{-6}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfcc09a07655df351485915d402798ea050c908d)

























![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)



























