數學/幾何/勾股定理著名定理

勾股定理：兩條直角邊上正方形的面積之和等於斜邊上正方形的面積。

在一個直角三角形中，斜邊的平方等於其他兩邊的平方和。符號上，對於直角三角形ABC，直角位於C，$AC^{2}+BC^{2}=AB^{2}$，或 $a^{2}+b^{2}=c^{2}$，其中c是斜邊。

歐幾里得的證明

此證明使用以下內容

• 直角的定義
• 平行的定義
• 正方形的定義
• 邊長為x的正方形的面積為x²
• 正方形的所有角都是直角
• 在同一點上，同一側與同一直線成直角的線段，在另一側形成一條直線
• 所有直角都相等
• 如果兩個三角形的兩邊和它們之間的角分別相等，則這兩個三角形全等
• 全等三角形的面積相等
• 三角形的面積是同一平行線之間同底邊平行四邊形面積的一半

歐幾里得在他的幾何原本第一卷命題47中給出了勾股定理的證明。

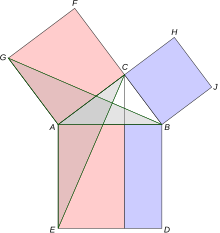
設ABC為直角三角形，直角位於C。構造正方形ABDE、ACFG和BCHJ，以及垂直於AB和ED的直線CKL。

考慮三角形GAB和CAE。對於這兩個三角形，邊GA和CA相等，因為它們是正方形ACFG的邊。同樣，邊AB和AE相等，因為它們是正方形ABDE的邊。此外，角GAB和CAE相等，因為它們都包含角CAB加上正方形的一個直角。因此，三角形GAB和CAE全等。

三角形GAB的面積是正方形ACFG的一半，因為它們共用邊GA，點B與正方形的對面FC共線。（這可以透過觀察將GAB剪下產生GAC來更清楚地看到，GAC的面積明顯是ACFG的一半，並且由於剪下保留面積，因此GAB的面積也是如此。）

同樣，三角形CAE的面積是矩形AKLE的一半，因為它們共用邊AE，點C與KL共線。

但GAB和CAE的面積相等。因此，正方形ACFG和矩形AKLE的面積相等。

用同樣的論證，正方形BCHJ的面積等於矩形BKLD的面積。兩個矩形AKLE和BKLD構成正方形ABDE，因此正方形ABDE的面積等於ACFG的面積加上BCHJ的面積。