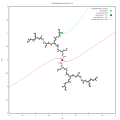
分形/複平面迭代/米休列維奇
米休列維奇點是引數 c(引數平面的點),其中臨界軌道是前週期的。
- 臨界後前週期引數
- "在米休列維奇點附近(它們只是可數的但稠密的),曼德勃羅集在區域性看起來像相應的朱利亞集,特別是它在每個米休列維奇點附近看起來非常不同。" 巴勃羅·施默金[1]
- 曼德勃羅集在臨界前週期米休列維奇點附近是漸近自相似的。
- 所有米休列維奇點的集合在曼德勃羅集邊界上是稠密的[2]
- 每個米休列維奇點都有一個乘數,它與螺旋的形狀有關。
- 每個米休列維奇點都被一個米休列維奇域包圍,在該域內,迭代受米休列維奇點的影響。
- 可以計算區域性米休列維奇域座標,它們在域的邊界處大小為 1。
- 可以估計米休列維奇域的大小。
以圈數為單位測量的有理角對應於落在曼德勃羅集的(前)週期點上的外部射線。它們方便地用二進位制表示。
外部角在角度加倍下的動力學與著陸點在迭代下的動力學不同:[3] 外部角和著陸米休列維奇點之間的前週期和週期可能不同
示例
- 外部角 0.1(0) 具有前週期 1 和週期 1,並且它落在點 c = −2 = 上(前週期 2 和週期 1)
- 外部角 .001001(010010100) 射線落在點 c = 0.026593792304386393+0.8095285579867694i 上。外部角具有前週期 6 和週期 9,但著陸點具有前週期 7 和週期 3
米休列維奇點(引數、多項式、對映)可以用以下符號標記:[4]
- 前週期和週期
- 引數座標 c ∈ M
- 角度 的外部射線
"Critically preperiodic polynomials are typically parameterized by the angle θ of the external ray landing at the critical value rather than by the critical value." MARY WILKERSON[5]
落在
- z = c 在 Julia 集 J(f) 上的動力平面
- 在引數平面上,曼德勃羅集 M 中的點 。
所以
引數射線的例子
- 角度為 的射線落在了引數平面的點 上。它是主天線尖端(1/2 肢的末端)。
- 角度為 的射線落在了引數平面的點 上。它是 1/3 尾跡的第一個尖端。
- 角度為 的射線落在了引數平面的點 上。它是 1/3 尾跡的最後一個尖端。
- 角度為 的射線落在了引數平面的點 上。它是 1/4 尾跡的中心點(分支點或中心點)。
- 角度為 的射線落在了引數平面的點 上。它是 1/3 尾跡的中心點(分支點或中心點)。
- 角度為 的射線落在了引數平面的點 上。它是 1/7 尾跡的中心點(分支點或中心點)。
在動態平面上,所有上述點 c(復二次多項式的引數)都會生成樹狀的 Julia 集。
動態平面根據與 kneading sequence 相關的動態射線進行分割槽。
-
1/4
-
1/6
-
9/56
-
129/16256
前週期和週期
[edit | edit source]
其中
- t 是前週期
- p 是週期
前週期有兩種含義
- T = 臨界點的預週期
- t = 臨界值的預週期
注意
臨界值和臨界點的週期 p 相同
預週期
- 臨界值的預週期
- "通常用臨界值外部射線的角度 θ 來引數化臨界預週期多項式,而不是用臨界值本身。" MARY WILKERSON[6]
- Wolf Jung 使用: "... 通常的約定是用臨界值的預週期。這樣做的好處是,臨界值的角度在倍增下具有與該點相同的預週期,並且在引數平面中可以找到相同角度。"
- 臨界點的預週期
- Pastor 使用臨界點的預週期: "所有 Misiurewicz 點的預週期都比它們的週期多 1,因此這個 被寫成 " [7]
- Demidov: libretexts:曼德勃羅集和朱利亞集的解剖(Demidov) 或 ibiblio
- Claude Heiland-Allen
點
[edit | edit source]型別
[edit | edit source]週期
[edit | edit source]Misiurewicz 點 c
拓撲
[edit | edit source]視覺型別:[9]
- 分支尖端 = 分支的端點[10] 或小島的尖端[11]
- 螺旋中心[12]
螺旋
[edit | edit source]-
Misiurewicz 點是 2 臂螺旋的中心
-
放大到對數螺旋
作為螺旋中心的 Misiurewicz 點可以根據轉動速度進行分類
- 快速[15]
- 緩慢
- 不轉:如果 Misiurewicz 點是實數,它根本不會轉動
螺旋也可以根據臂的數量進行分類。
Each Misiurewicz point has a multiplier which is related to the shape of the spiral.[16]
外部射線數量
[edit | edit source]- 端點 = 尖端 = 1 個角度
- 原始型別 = 原始迴圈的 2 個角度
- 衛星型別 = 衛星迴圈的 2 個或多個角度
前週期和週期
[edit | edit source]通常,預週期臨界值具有預週期 k、週期 p、射線週期 rp 和 v 個角度。有三種情況:
- 尖端:r = 1,v = 1
- 原始:r = 1,v = 2
- 衛星:r > 1,v = r
嵌入式朱利亞集中的結構性 Misiurewicz 點都具有相同的週期,即影響島的週期。 [17]
尖端
- "似乎主螺旋的第 n 長臂的尖端具有周期 n(從 1 開始計數),並且一些細絲的尖端具有周期 1" Claude Heiland-Allen [18]
- 並非所有端點都有預週期 1 或週期 1
命名型別
[edit | edit source]主 Misiurewicz 點 肢體 :[19]
- 有 m 個外部角,這些外部角是 外部角的(在翻倍下)原像。
曼德勃羅集混沌帶的特徵 Misiurewicz 點是:[20]
- 混沌帶中最突出、最明顯的 Misiurewicz 點
- 與該帶的週期相同
- 與該帶基因的週期相同
- 帶合併點 = 合併兩個 混沌帶 和 的點
例子:[21]
- = 主天線的頂端,外部角 = 1/2[22]
- ,外部角為 5 和 7/12
- ,外部角為 33 和 47/80
- ,外部角為 1795 和 2557/4352
- ...
- = 費根鮑姆點 = MF = 米爾貝格-費根鮑姆
以文字形式
double m[12] = {
-2.0,
-1.543689012692076,
-1.430357632451307,
-1.407405118164702,
-1.402492176358564,
-1.401441494253588,
-1.401216504309415,
-1.401168320839301,
-1.401158001505211,
-1.401155791424613,
-1.401155318093230,
-1.401155216720152
};
const complex double cf = -1.401155189093314712; //the Feigenbaum point -1.401155 = m[infinity]
- 樹形分隔符(樹是帶的子集)
- 沒有與帶相同的週期
米修列維奇點,是曼德勃羅集的一部分
- 中心 0.4244 + 0.200759i;最大迭代次數 100;檢視半徑 0.00479616 [23]

尾跡的重要點
- 結合點 = 週期 1 和 2 分量之間的根點 = c = -0.75 = -3/4 = 內部角 1/2 的分叉點 = 2 個外部射線 1/3 和 2/3 的著陸點 = 1/2 尾跡 的起點
- 週期 2 的核(分量的中心)= c = -1
- 主天線的尖端 c = -2 = . 它也是角度為 的外部射線的著陸點
- c = -1.543689012692076 = 1/2 尾跡的主米修列維奇點 = 尾跡的主節點(分支點)= = 外部射線 5/12 和 7/12 的著陸點
對於
- 復二次函式 f(z) = z^2 + c,分支點是米修列維奇點(簡單點而不是島嶼)
- 復三次函式 f(z) = z^3 + c 這裡有島嶼(迷你曼德勃羅集)。例如縮放:c = -0.574891209746913 +0.716327145043763 i
無論是 M2 還是 M3,米修列維奇點都有有限數量的分支,而雙曲分量有無限數量的天線。
然而,每個 M3 中的小的多重勃羅集都有兩個 1/2 長的肢體,而每個小曼德勃羅集只有一個。
多重勃羅集的乘數對映:這裡它是一個 2 對 1 的對映,對於每個內部角,都有兩個邊界點。
特別是,從分量到圓盤的共形對映類似於乘數的平方根。
- 曼德勃羅集演示 第 6 頁 1
"The legendary colour palette technique embeds an image in the iteration bands of an escape time fractal by linearizing it by scanlines and synchronizing the scan rate to the iterations in the fractal spirals so they line up to reconstruct the original image. Historically this has been done by preparing palettes for fractal software using external tools, and mostly only for small images (KF for example has a palette limited to 1024 colour slots). Kalles Fraktaler 2 has an image texture feature, which historically only allowed you to warp a background through the semi-transparent fractal. I added the ability to create custom colouring algorithms in OpenGL shader language (GLSL), with which it is possible to repurpose this texture and (for example) use it as a legendary palette. Here I scaled my avatar (originally 256x256) to 128x16 pixels, and fine tuned the iteration count divisor by hand after zooming to a spiral in the Seahorse Valley of the Mandelbrot set. Then the face from the icon is visible in the spirals all the way down to the end of the video. I used a work-in-progress (not yet released) build of KF 2.15.3, which has a new setting not to resize the texture to match the frame size: this allows the legendary technique to work much more straightforwardly. I rendered exponential map EXR frames from KF and assembled into a zoom video with zoomasm. From KF I exported just the RGB channels with the legendary palette colouring, and the distance estimate channels. I did not colour the RGB with the distance estimate in KF, because with the exponential map transformation they would not be screen-space correct (the details would be smaller in the center of the reprojected video than at the edges). I could not do all the colouring in zoomasm either, because it does not support image textures. I added the boundary of the fractal in zoomasm afterwards, by mixing pink with the RGB from KF according to the length of the screen-space distance estimate channels (which zoomasm scales properly when reprojecting the exponential map)." Claude Heiland-Allen[24]
- fractalforums.org: misiurewicz-points-in-the-multibrot
- 多項式對映的Misiurewicz點和橫截性,作者:Benjamin Hutz,Arxiv:於2013年9月16日提交(v1),最後修訂於2014年8月8日(此版本,v2)] Adam Towsley。
- marcm200文章中的兩個錯誤
- 第2頁,phi_f,n(z)的定義缺少每個乘積項中的減法-z。
- 對於m=0,廣義dynatomic公式沒有很好地定義,在這種情況下它應該與經典dynatomic多項式相同。)
marcm200的maxima指令碼,使用主函式misiurewicz_multibrot_dmn(d,m,n)來表示度數為d、前週期為m、週期為n的多重分形。
kill(all);
numer:false;
display2d:false;
/* general dynatomic polynomial to arrive at Misiurewicz points for the quadratic or higher degree Mandelbrot set */
/* based on: B Hitz, A Towsley. Misiurewicz points for polynomial maps and transversality, 2014. */
/* n-fold composition */
composition_fn(f,n) := (
ret:"Error. ,composition_fn",
if n = 0 then ret:z
else if n > 0 then (
ret:f,
for i from 2 thru n do (
ret:subst(f,z,ret)
)
) else print("Error. composition_fn"),
ratsimp(ret)
)$
/* the dynatomic polynomial */
dynatomic_fz0n(f,z0,n) := (
erg:"Error. dynatomic_fz0n",
if n < 1 then (
erg:"Error. Period must be at least 1.",
print("Error. Period must be at least 1.")
) else (
erg:1,
for k from 1 thru n do (
if mod(n,k) = 0 then (
co:composition_fn(f,k),
co:subst(z0,z,co),
erg: erg * ( ( co - z0 ) ^ moebius(n/k) )
)
)
),
ratsimp(erg)
)$
/* generalized dynatomic polynomial */
general_dynatomic_fz0mn(f,z0,m,n) := (
ret:"Error. general_dynatomic_fz0mn",
if m = 0 and n > 0 then (
ret: dynatomic_fz0n(f, z , n)
) else if m > 0 and n > 0 then (
ret: ratsimp(
dynatomic_fz0n(f, composition_fn(f,m) , n)
/
dynatomic_fz0n(f, composition_fn(f,m-1) , n)
),
ret:subst(z0,z,ret)
) else print("Error. general_dynatomic_fz0mn"),
ratsimp(ret)
)$
/* Misiurewicz points for unicritical multibrot z^d+c with exact preperiod m and period n*/
misiurewicz_multibrot_dmn(d,m,n) := (
numer:false,
ret: "Error misiurewicz_multibrot_dmn",
if m > 0 and n > 0 and d >= 2 then (
ret1: general_dynatomic_fz0mn(z^d+c,z,m,n),
ret1: ratsimp(subst(0,z,ret)),
if m # 0 and mod(m-1,n) = 0 then (
ret2: general_dynatomic_fz0mn(z^d+c,z,0,n),
ret2: subst(0,z,ret2) ^ (d-1),
ret: ret1 / ret2
) else ret: ret1
) else print("Error misiurewicz_multibrot_dmn"),
ret:ratsimp(ret),
print("Misiurewicz points as solution from"),
print(ret,"= 0"),
sol:solve(ret=0,c),
numer:true,
for i from 1 thru length(sol) do (
print("solution",realpart(expand(rhs(sol[i])))," + i*", imagpart(expand(rhs(sol[i]))) )
)
)$
- math.stackexchange問題:counting-misiurewicz-points
- Claude Heiland-Allen對Misiurewicz點的列舉
- "……我們不知道如何計算(……)二次有理對映族的Misiurewicz引數(具有較高(前)週期)。可能需要一種非嚴格的方法來在合理的時間內找到Misiurewicz引數,例如Biham-Wenzel方法。" HIROYUKI INOU [25]
- 線上整數序列百科全書 (OEIS)
- 據說是 A000740
- 似乎是 A038199
- 似乎是 A000225
- 似乎是 A166920
- 來自 多項式對映的Misiurewicz點和橫截性,作者:Benjamin Hutz,Adam Towsley 的推論 3.3。
對於 , Misiurewicz點的數量是
其中
- m 是
- n 是
- d 是 函式的度數
- 是 自然數 n 的莫比烏斯函式
- 是 對所有正整數 除以 的和。
實現
復二次對映的 Misiurewicz 點
[edit | edit source]- 數值方法
- 求解方程
- 找到具有預週期角度的外部射線的著陸點
- 圖形方法
- Misiurewicz 域
"the best way of being sure you get to the correct point is to trace an external ray with the correct external angle, until you reach close enough (for example, the ray point has a tiny imaginary part, as these points are all on the real axis). then use Newton's method starting from the ray point." Claude Heiland-Allen[26]
跟蹤射線
[edit | edit source]- "使用所有 4 種方法跟蹤預週期 + 週期 ~= 500 到駐點 ~1000 的射線,並改變銳度" [27]
- "我透過跟蹤每個預週期和週期總和小於或等於 16 的預週期射線來建立資料庫。我將射線跟蹤到雙精度極限,在我的四核桌上型電腦上平均每秒跟蹤 400 條射線。然後,我將著陸在相同點(或附近,具有很小的閾值半徑)的射線分組在一起。我只將具有相同週期和預週期的射線分組在一起..."[28]
Misiurewicz 域
[edit | edit source]求解方程
[edit | edit source]多項式的根
[edit | edit source]Misiurewicz 點 [29] 是特殊的邊界點。
在 Maxima CAS 中定義 多項式
P(n):=if n=0 then 0 else P(n-1)^2+c;
定義一個 Maxima CAS 函式,其根是 Misiurewicz 點,並找到它們。
M(preperiod,period):=allroots(%i*P(preperiod+period)-%i*P(preperiod));
使用示例
(%i6) M(2,1); (%o6) [c=-2.0,c=0.0] (%i7) M(2,2); (%o7) [c=-1.0*%i,c=%i,c=-2.0,c=-1.0,c=0.0]
分解多項式
[edit | edit source]"分解確定 Misiurewicz 點的多項式。我相信你應該從
( f^(p+k-1) (c) + f^(k-1) (c) ) / c
這應該已經具有確切的預週期 k,但週期是 p 的任何因數。所以它應該進一步分解以獲得週期。
例如:對於預週期 k = 1 和週期 p = 2,我們有
c^3 + 2c^2 + c + 2 .
這分解為
(c + 2)*(c^2 + 1)
用於週期 1 和 2。我猜這些因子恰好出現一次,並且沒有其他因子,但我不知道。"Wolf Jung
牛頓方法
[edit | edit source]著陸在 Misiurewicz 點上的射線的外部角度
[edit | edit source]方法
- 跟蹤預週期射線(到雙精度極限)[30]
- 使用 Devaney 演算法計算喚醒 p/q 的主 Misiurewicz 點的外部角度
- 列舉二進位制字串
另見
外部角度的預週期/週期與 Misurewicz 點之間的關係:[31] 預週期和週期在外部角度和著陸 Misiurewicz 點之間可能不同
外部角度在角度加倍下的動力學與著陸點在迭代下的動力學不同!!!
示例
- 外部角 0.1(0) 具有前週期 1 和週期 1,並且它落在點 c = −2 = 上(前週期 2 和週期 1)
- 外部角 .001001(010010100) 射線落在點 c = 0.026593792304386393+0.8095285579867694i 上。外部角具有前週期 6 和週期 9,但著陸點具有前週期 7 和週期 3
列舉二進位制字串
[edit | edit source]要找到著陸在 Misiurewicz 點 上的外部角度
列舉長度為 n = 預週期 + 週期的二進位制字串,其中有 2^n 個,然後丟棄在規範化時具有不同(預)週期的字串。
示例:預週期 1,週期 2
- 有 2^(1 + 2) = 2^3 = 8 個候選者
- .000 = 0
- .001
- .010
- .011
- .100
- .101
- .110
- .111
示例:週期 = 2,預週期 = 5
- 有 2^(2 + 5) = 2^7 = 128 個候選者
- 其中一半可以立即消除,因為週期 ...(00) 和 ...(11) 的 4 個長度為 2 的字串簡化為 ...(0) 和 ...(1)(即,它們具有周期 1 而不是 2)。剩下 64 個
- 考慮最後一個預週期數字:如果它與最後一個週期數字相同,則真正的預週期更小(將週期部分向左移動)。所以另一半被消除,只剩下最後 3 個數字的可能性為 ...0(01) 和 ...1(10)。剩下 32 個
- 由於曼德爾布羅特集是對稱的,你只需要考慮上半平面的射線,它們以 .0... 開頭,這消除了另一半:剩下 16 個
你想要週期加倍級聯的主要費根鮑姆點之外的射線,其角度為 .01 10 1001 10010110 ...(非重複,無理數,與圖厄-摩斯序列相關)。因此,數字必須嚴格介於這兩個數字之間
- .0110100
- .0111111
列舉它們得到
- .01101(10)
- .01110(01)
- .01111(10)
所以剩下 3 個候選者。跟蹤外部射線得到這些座標
- -1.6975553932375476
- -1.8186201342243300
- -1.9935450866059059
這些都不在你的序列中,現在我記得在 z^2+c 的迭代下,Misiurewicz 點的(預)週期不必與角度在角度加倍模 1 轉下的(預)週期對應...
答案可能是“調整”,即找到第一個分離點的角度,然後透過週期加倍級聯的外部角度對來調整它們。
天線的頂端具有外部角度 .0(1) = .1(0) : 跟蹤給出 -2,週期 2 球具有外部角度 .(01) 和 .(10),將每個 0 替換為 01,將 1 替換為 10,給出週期 2 球輻條頂端的外部角度: .01(10) 和 .10(01) : 跟蹤給出 -1.5436890126920764 重複,給出週期 4 球輻條的頂端 .0110(1001) 和 .1001(1001) : 跟蹤給出 -1.4303576324513074 重複,這將給出使用雙精度跟蹤的射線端點的表(所有射線端點的虛部都小於 1e-9)
- -2
- -1.5436890126920764
- -1.4303576324513074
- -1.4074051181647029
- -1.4024921763585667
- -1.4014414942535918
- -1.4012165015160745
- ↑ mathoverflow 問題: 是否存在某種已知方法來建立曼德勃羅集的邊界?
- ↑ 某些無限重整化的點的曼德勃羅集的區域性連通性,作者:姜雲平
- ↑ Misiurewicz 點的外部角度,作者:克勞德·海蘭德-艾倫
- ↑ 來自二次函式交配的有限細分規則: 存在和構建,作者:瑪麗·伊麗莎白·威爾克森
- ↑ 對臨界前週期二次交配的細分規則構建,作者:瑪麗·威爾克森
- ↑ 對臨界前週期二次交配的細分規則構建,作者:瑪麗·威爾克森
- ↑ [https://www.hindawi.com/journals/ddns/2007/045920/ G. Pastor, M. Romera, G. Alvarez, J. Nunez, D. Arroyo, F. Montoya, "使用杜瓦迪和赫伯德的外部引數操作",自然與社會中的離散動力學,第 2007 卷,文章 ID 045920,17 頁,2007 年。 https://doi.org/10.1155/2007/45920]
- ↑ W Jung : 曼德勃羅集邊界的同胚,2002 年博士論文
- ↑ 耶魯大學的分形幾何,作者:邁克爾·弗雷姆、貝努瓦·曼德勃羅(1924-2010)和尼爾·內格,2013 年 2 月 2 日
- ↑ 終點 作者:羅伯特·P·穆納福,2008 年 3 月 9 日。
- ↑ mathoverflow 問題 : 除了簡單地四處尋找之外,是否存在一種方法來查詢曼德勃羅集中深度區域?
- ↑ math.stackexchange 問題 : 用於縮放曼德勃羅集中心的數值
- ↑ 一維二次對映點的符號序列,作者:G Pastor、Miguel Romera、Fausto Montoya Vitini
- ↑ 分支點 作者:羅伯特·P·穆納福,1997 年 11 月 19 日。
- ↑ 書 : 課堂的分形:第二部分:複雜系統和曼德勃羅集,第 461 頁,作者:海因茨-奧托·佩特根、哈特穆特·尤爾根斯、迪特馬爾·索普
- ↑ m-describe,作者:克勞德·海蘭德-艾倫
- ↑ fractalforums.org : 尋找 Misiurewicz 點
- ↑ Misiurewicz 域,作者:克勞德·海蘭德-艾倫
- ↑ 曼德勃羅集的同胚子集族,作者:沃爾夫·容,第 7 頁
- ↑ G. Pastor, M. Romera, G. Álvarez, D. Arroyo 和 F. Montoya, "論曼德勃羅集中的週期性和混沌區域",混沌、孤立子與分形,第 32 卷(2007 年)15-25
- ↑ 一維二次對映中的等於 1 的縮放常數,作者:M. ROMERA、G. PASTOR 和 F. MONTOYA
- ↑ G. Pastor, M. Romera, G. Álvarez 和 F. Montoya, "在曼德勃羅集天線中使用外部引數操作",物理學 D,第 171 卷(2002 年),52-71
- ↑ 示例
- ↑ 傳奇調色盤,作者:mathr
- ↑ 三次多項式族的分岔軌跡的視覺化,作者:井上博之
- ↑ fractalforums.org : 曼德勃羅集實切片的初級分隔符-Misiurewicz 點
- ↑ 外部射線跟蹤,作者:克勞德·海蘭德-艾倫
- ↑ Misiurewicz 點的外部角度,作者:克勞德·海蘭德-艾倫
- ↑ 維基百科中的 Misiurewicz 點
- ↑ Misiurewicz 點的外部角度,作者:克勞德·海蘭德-艾倫
- ↑ Misiurewicz 點的外部角度,作者:克勞德·海蘭德-艾倫