本文描述了週期點 的某些復二次對映 。一個對映 是根據變數本身的先前值或值計算變數值的公式;一個二次 對映是涉及先前值被提升到冪 一和二的對映;一個復 對映是一個變數和引數都是複數 的對映。一個週期點 是指對映中變數的值,該值在固定長度的間隔後會重複出現。
這些週期點在法圖 和朱利亞集 理論中發揮著作用。
讓
f c ( z ) = z 2 + c {\displaystyle f_{c}(z)=z^{2}+c\,} 是復二次對映 ,其中 z {\displaystyle z} c {\displaystyle c} 複數 。
在符號上, f c ( k ) ( z ) {\displaystyle f_{c}^{(k)}(z)} k {\displaystyle k} 複合 的 f c {\displaystyle f_{c}} k {\displaystyle k} 導數 的 f c {\displaystyle f_{c}} f c . {\displaystyle f_{c}.} k 次迭代 之後的的值。因此
f c ( k ) ( z ) = f c ( f c ( k − 1 ) ( z ) ) . {\displaystyle f_{c}^{(k)}(z)=f_{c}(f_{c}^{(k-1)}(z)).} 復二次對映的週期 為 p {\displaystyle p} 動力學平面 上的點 z {\displaystyle z}
f c ( p ) ( z ) = z , {\displaystyle f_{c}^{(p)}(z)=z,} 其中 p {\displaystyle p} 整數 。
我們可以引入一個新函式
F p ( z , f ) = f c ( p ) ( z ) − z , {\displaystyle F_{p}(z,f)=f_{c}^{(p)}(z)-z,} 所以週期點是 零點 函式 F p ( z , f ) {\displaystyle F_{p}(z,f)}
F p ( z , f ) = 0 , {\displaystyle F_{p}(z,f)=0,} 這是一個 次數 為 2 p . {\displaystyle 2^{p}.}
描述週期點的多項式 F p ( z , f ) {\displaystyle F_{p}(z,f)} 次數 為 d = 2 p {\displaystyle d=2^{p}} 代數基本定理 它正好有 d = 2 p {\displaystyle d=2^{p}} 重數 。
水平軸上週期點的穩定性指標 引數平面區域的邊界,這些區域具有周期為 1-6 的吸引軌道 基於 復二次多項式 的離散動力系統的臨界軌道。它趨向於弱 吸引 的 不動點 ,其中 abs(乘子) = 0.99993612384259 有理對映 f {\displaystyle f} z 0 {\displaystyle z_{0}} p {\displaystyle p} m ( f p , z 0 ) = λ {\displaystyle m(f^{p},z_{0})=\lambda }
m ( f p , z 0 ) = λ = { f p ′ ( z 0 ) , if z 0 ≠ ∞ 1 f p ′ ( z 0 ) , if z 0 = ∞ {\displaystyle m(f^{p},z_{0})=\lambda ={\begin{cases}f^{p\prime }(z_{0}),&{\mbox{if }}z_{0}\neq \infty \\{\frac {1}{f^{p\prime }(z_{0})}},&{\mbox{if }}z_{0}=\infty \end{cases}}} 其中 f p ′ ( z 0 ) {\displaystyle f^{p\prime }(z_{0})} f p {\displaystyle f^{p}} z {\displaystyle z} z 0 {\displaystyle z_{0}} 導數 。
由於乘數在給定軌道上的所有周期點處都相同,因此被稱為週期 軌道 的乘數。
乘數為
一個複數;
在任何有理對映在其不動點處的共軛下是不變的;[ 1]
用於檢查週期點(也包括不動點)的穩定性,其 **穩定性指數** 為 a b s ( λ ) . {\displaystyle abs(\lambda ).\,} 週期點[ 2]
當 a b s ( λ ) < 1 ; {\displaystyle abs(\lambda )<1;} 當 a b s ( λ ) = 0 ; {\displaystyle abs(\lambda )=0;}
當 0 < a b s ( λ ) < 1 ; {\displaystyle 0<abs(\lambda )<1;}
當 a b s ( λ ) = 1 ; {\displaystyle abs(\lambda )=1;} 當 λ {\displaystyle \lambda } 單位根 時,為有理中性點或拋物線點;
無理中性點 當 a b s ( λ ) = 1 {\displaystyle abs(\lambda )=1}
當 a b s ( λ ) > 1. {\displaystyle abs(\lambda )>1.} 週期點
是吸引點的,總是位於 Fatou 集 中;
是排斥點的,位於 Julia 集中;
是中性不動點的,可能位於其中一個或另一個。[ 3] solve these equations using numerical methods for solving polynomials - and even something simple such as Newton's method is going to converge a lot faster than finding the cycles just by iterating a single point (as is how bifurcations diagrams are usually made) under fc itself. Milo Brandt[ 4]
方法
首先,讓我們找出經過一次應用 f {\displaystyle f} f c ( z ) = z {\displaystyle f_{c}(z)=z}
z 2 + c = z , {\displaystyle z^{2}+c=z,\,} 可以改寫為:
z 2 − z + c = 0. {\displaystyle \ z^{2}-z+c=0.} 由於這是一個關於單個未知數的一般 二次方程 ,我們可以應用 標準二次方程求解公式
α 1 = 1 − 1 − 4 c 2 {\displaystyle \alpha _{1}={\frac {1-{\sqrt {1-4c}}}{2}}} α 2 = 1 + 1 − 4 c 2 . {\displaystyle \alpha _{2}={\frac {1+{\sqrt {1-4c}}}{2}}.} 因此,對於 c ∈ C ∖ { 1 / 4 } {\displaystyle c\in \mathbb {C} \setminus \{1/4\}} α 1 {\displaystyle \alpha _{1}} α 2 {\displaystyle \alpha _{2}}
由於
α 1 = 1 2 − m {\displaystyle \alpha _{1}={\frac {1}{2}}-m} α 2 = 1 2 + m {\displaystyle \alpha _{2}={\frac {1}{2}}+m} m = 1 − 4 c 2 , {\displaystyle m={\frac {\sqrt {1-4c}}{2}},} 我們有 α 1 + α 2 = 1 {\displaystyle \alpha _{1}+\alpha _{2}=1}
因此,不動點關於 z = 1 / 2 {\displaystyle z=1/2}
此圖顯示了不動點(均為排斥不動點)。 沿水平軸的 c 的不動點 F(z ) = z *z 的 Fatou 集 ,並標出了不動點 這裡通常使用不同的符號:[ 5]
α c = 1 − 1 − 4 c 2 {\displaystyle \alpha _{c}={\frac {1-{\sqrt {1-4c}}}{2}}} λ α c = 1 − 1 − 4 c {\displaystyle \lambda _{\alpha _{c}}=1-{\sqrt {1-4c}}} 以及
β c = 1 + 1 − 4 c 2 {\displaystyle \beta _{c}={\frac {1+{\sqrt {1-4c}}}{2}}} λ β c = 1 + 1 − 4 c . {\displaystyle \lambda _{\beta _{c}}=1+{\sqrt {1-4c}}.} 我們再次得到
α c + β c = 1. {\displaystyle \alpha _{c}+\beta _{c}=1.} 不動點之間的距離
1 − Δ 2 < 1 2 < 1 + Δ 2 {\displaystyle {\frac {1-\Delta }{2}}<{\frac {1}{2}}<{\frac {1+\Delta }{2}}} 是 delta Δ {\displaystyle \Delta }
其中
Δ = 1 − 4 c {\displaystyle \Delta ={\sqrt {1-4c}}} 對於 c = 1 4 {\displaystyle c={\frac {1}{4}}} Δ ( 1 4 ) = 0 = 0 {\displaystyle \Delta ({\frac {1}{4}})={\sqrt {0}}=0}
對於 c = 0 {\displaystyle c=0} Δ ( 1 ) = 1 = 1 {\displaystyle \Delta (1)={\sqrt {1}}=1}
由於 關於 *z* 的導數 為
P c ′ ( z ) = d d z P c ( z ) = 2 z , {\displaystyle P_{c}'(z)={\frac {d}{dz}}P_{c}(z)=2z,} 我們有
P c ′ ( α c ) + P c ′ ( β c ) = 2 α c + 2 β c = 2 ( α c + β c ) = 2. {\displaystyle P_{c}'(\alpha _{c})+P_{c}'(\beta _{c})=2\alpha _{c}+2\beta _{c}=2(\alpha _{c}+\beta _{c})=2.} 這意味著 P c {\displaystyle P_{c}}
這些點透過以下事實來區分
β c {\displaystyle \beta _{c}} 角度為 0 時,外部射線 的著陸點,其中 c ∈ M ∖ { 1 / 4 } {\displaystyle c\in M\setminus \left\{1/4\right\}}
Julia 集的最排斥不動點。
位於右側(當不動點在實軸 上不對稱時),它是連線 Julia 集的最右端點(除花椰菜外)。[ 6] α c {\displaystyle \alpha _{c}} 幾條射線的著陸點。
當 c {\displaystyle c}
在 Mandelbrot 集的肢體根點是拋物線的。
對於 c {\displaystyle c} 特殊情況
二次對映的一個重要情況是 c = 0 {\displaystyle c=0} α 1 = 0 {\displaystyle \alpha _{1}=0} α 2 = 1 {\displaystyle \alpha _{2}=1} 不動點 ,而 1 屬於Julia 集 。
只有一個不動點
我們有 α 1 = α 2 {\displaystyle \alpha _{1}=\alpha _{2}} 1 − 4 c = 0. {\displaystyle 1-4c=0.} c = 1 / 4 , {\displaystyle c=1/4,} α 1 = α 2 = 1 / 2 {\displaystyle \alpha _{1}=\alpha _{2}=1/2} c = 1 / 4 {\displaystyle c=1/4} 實 值。
我們可以透過新增無窮大 將複平面 C {\displaystyle \mathbb {C} } 黎曼球面(擴充套件複平面) C ^ {\displaystyle \mathbb {\hat {C}} }
C ^ = C ∪ { ∞ } {\displaystyle \mathbb {\hat {C}} =\mathbb {C} \cup \{\infty \}} 並擴充套件 f c {\displaystyle f_{c}} f c ( ∞ ) = ∞ . {\displaystyle f_{c}(\infty )=\infty .}
那麼無窮大 是
超吸引
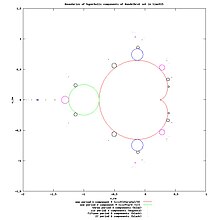
f c {\displaystyle f_{c}} [ 7] f c ( ∞ ) = ∞ = f c − 1 ( ∞ ) . {\displaystyle f_{c}(\infty )=\infty =f_{c}^{-1}(\infty ).} 從週期 1 到 2 的分岔 復二次對映 fc(z)=z*z +c 中週期點從週期 1 到 2 的分岔 2 週期迴圈是兩個不同的點 β 1 {\displaystyle \beta _{1}} β 2 {\displaystyle \beta _{2}} f c ( β 1 ) = β 2 {\displaystyle f_{c}(\beta _{1})=\beta _{2}} f c ( β 2 ) = β 1 {\displaystyle f_{c}(\beta _{2})=\beta _{1}}
f c ( f c ( β n ) ) = β n {\displaystyle f_{c}(f_{c}(\beta _{n}))=\beta _{n}} 對於 n ∈ { 1 , 2 } {\displaystyle n\in \{1,2\}}
f c ( f c ( z ) ) = ( z 2 + c ) 2 + c = z 4 + 2 c z 2 + c 2 + c . {\displaystyle f_{c}(f_{c}(z))=(z^{2}+c)^{2}+c=z^{4}+2cz^{2}+c^{2}+c.} 將此等式設定為z ,我們得到
z 4 + 2 c z 2 − z + c 2 + c = 0. {\displaystyle z^{4}+2cz^{2}-z+c^{2}+c=0.} 此方程是 4 次多項式,因此有四個(可能不不同的)解。但是,我們已經知道兩個解。它們是 α 1 {\displaystyle \alpha _{1}} α 2 {\displaystyle \alpha _{2}} f {\displaystyle f} f {\displaystyle f}
因此,我們的 4 次多項式可以用兩種方式分解
( z − α 1 ) ( z − α 2 ) ( z − β 1 ) ( z − β 2 ) = 0. {\displaystyle (z-\alpha _{1})(z-\alpha _{2})(z-\beta _{1})(z-\beta _{2})=0.\,} 這直接擴充套件為 x 4 − A x 3 + B x 2 − C x + D = 0 {\displaystyle x^{4}-Ax^{3}+Bx^{2}-Cx+D=0}
D = α 1 α 2 β 1 β 2 , {\displaystyle D=\alpha _{1}\alpha _{2}\beta _{1}\beta _{2},\,} C = α 1 α 2 β 1 + α 1 α 2 β 2 + α 1 β 1 β 2 + α 2 β 1 β 2 , {\displaystyle C=\alpha _{1}\alpha _{2}\beta _{1}+\alpha _{1}\alpha _{2}\beta _{2}+\alpha _{1}\beta _{1}\beta _{2}+\alpha _{2}\beta _{1}\beta _{2},\,} B = α 1 α 2 + α 1 β 1 + α 1 β 2 + α 2 β 1 + α 2 β 2 + β 1 β 2 , {\displaystyle B=\alpha _{1}\alpha _{2}+\alpha _{1}\beta _{1}+\alpha _{1}\beta _{2}+\alpha _{2}\beta _{1}+\alpha _{2}\beta _{2}+\beta _{1}\beta _{2},\,} A = α 1 + α 2 + β 1 + β 2 . {\displaystyle A=\alpha _{1}+\alpha _{2}+\beta _{1}+\beta _{2}.\,} 我們已經有兩個解,只需要另外兩個。因此問題相當於求解一個二次多項式。特別注意,
α 1 + α 2 = 1 − 1 − 4 c 2 + 1 + 1 − 4 c 2 = 1 + 1 2 = 1 {\displaystyle \alpha _{1}+\alpha _{2}={\frac {1-{\sqrt {1-4c}}}{2}}+{\frac {1+{\sqrt {1-4c}}}{2}}={\frac {1+1}{2}}=1} 以及
α 1 α 2 = ( 1 − 1 − 4 c ) ( 1 + 1 − 4 c ) 4 = 1 2 − ( 1 − 4 c ) 2 4 = 1 − 1 + 4 c 4 = 4 c 4 = c . {\displaystyle \alpha _{1}\alpha _{2}={\frac {(1-{\sqrt {1-4c}})(1+{\sqrt {1-4c}})}{4}}={\frac {1^{2}-({\sqrt {1-4c}})^{2}}{4}}={\frac {1-1+4c}{4}}={\frac {4c}{4}}=c.} 將這些加到上面,我們得到 D = c β 1 β 2 {\displaystyle D=c\beta _{1}\beta _{2}} A = 1 + β 1 + β 2 {\displaystyle A=1+\beta _{1}+\beta _{2}} f {\displaystyle f}
D = c β 1 β 2 = c 2 + c {\displaystyle D=c\beta _{1}\beta _{2}=c^{2}+c} A = 1 + β 1 + β 2 = 0. {\displaystyle A=1+\beta _{1}+\beta _{2}=0.} 由此,我們很容易得到
β 1 β 2 = c + 1 {\displaystyle \beta _{1}\beta _{2}=c+1} β 1 + β 2 = − 1 {\displaystyle \beta _{1}+\beta _{2}=-1} 從這裡,我們構造一個以 A ′ = 1 , B = 1 , C = c + 1 {\displaystyle A'=1,B=1,C=c+1}
β 1 = − 1 − − 3 − 4 c 2 {\displaystyle \beta _{1}={\frac {-1-{\sqrt {-3-4c}}}{2}}} β 2 = − 1 + − 3 − 4 c 2 . {\displaystyle \beta _{2}={\frac {-1+{\sqrt {-3-4c}}}{2}}.} 仔細觀察表明
f c ( β 1 ) = β 2 {\displaystyle f_{c}(\beta _{1})=\beta _{2}} f c ( β 2 ) = β 1 , {\displaystyle f_{c}(\beta _{2})=\beta _{1},} 這意味著這兩個點是單個週期為 2 的迴圈上的兩個點。
我們可以使用 多項式長除法 將因子 ( z − α 1 ) {\displaystyle (z-\alpha _{1})} ( z − α 2 ) , {\displaystyle (z-\alpha _{2}),} α 1 {\displaystyle \alpha _{1}} α 2 {\displaystyle \alpha _{2}}
( z 2 + c ) 2 + c − z = ( z 2 + c − z ) ( z 2 + z + c + 1 ) . {\displaystyle (z^{2}+c)^{2}+c-z=(z^{2}+c-z)(z^{2}+z+c+1).\,} 第一個因式的根是兩個不動點。它們在主心形之外是排斥的。
第二個因式有兩個根
− 1 ± − 3 − 4 c 2 . {\displaystyle {\frac {-1\pm {\sqrt {-3-4c}}}{2}}.\,} 這兩個根,與第一種方法找到的相同,形成了週期為 2 的軌道。[ 8]
再次,讓我們看看 c = 0 {\displaystyle c=0}
β 1 = − 1 − i 3 2 {\displaystyle \beta _{1}={\frac {-1-i{\sqrt {3}}}{2}}} β 2 = − 1 + i 3 2 , {\displaystyle \beta _{2}={\frac {-1+i{\sqrt {3}}}{2}},} 它們都是複數。我們有 | β 1 | = | β 2 | = 1 {\displaystyle |\beta _{1}|=|\beta _{2}|=1} c = − 1 {\displaystyle c=-1} β 1 = 0 {\displaystyle \beta _{1}=0} β 2 = − 1 {\displaystyle \beta _{2}=-1}
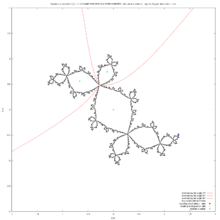
f (z ) = z *z −0.75 的週期為 6 的週期點作為 2 個隱式曲線的交點方程 f ( n ) ( z ) = z {\displaystyle f^{(n)}(z)=z} n
不存在 五次或更高次的多項式方程的 根式解 ,因此,一般情況下,週期大於 2 的迴圈上的點必須使用 數值方法 計算。但是,在週期為 4 的特定情況下,迴圈點具有根式解的冗長表示式。[ 9]
當 c = –2 時,所有周期的週期點都存在三角函式解。情況 z n + 1 = z n 2 − 2 {\displaystyle z_{n+1}=z_{n}^{2}-2} 邏輯斯諦對映 情況 r = 4: x n + 1 = 4 x n ( 1 − x n ) . {\displaystyle x_{n+1}=4x_{n}(1-x_{n}).} z = 2 − 4 x . {\displaystyle z=2-4x.} x 的 k 迴圈之一(所有迴圈都是排斥的)是
sin 2 ( 2 π 2 k − 1 ) , sin 2 ( 2 ⋅ 2 π 2 k − 1 ) , sin 2 ( 2 2 ⋅ 2 π 2 k − 1 ) , sin 2 ( 2 3 ⋅ 2 π 2 k − 1 ) , … , sin 2 ( 2 k − 1 2 π 2 k − 1 ) . {\displaystyle \sin ^{2}\left({\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2\cdot {\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2^{2}\cdot {\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2^{3}\cdot {\frac {2\pi }{2^{k}-1}}\right),\dots ,\sin ^{2}\left(2^{k-1}{\frac {2\pi }{2^{k}-1}}\right).}
為了建立曼德布羅集的週期性分量,對於 f c ( z ) = z 2 + c {\displaystyle f_{c}(z)=z^{2}+c}
從 z 0 := 0 {\displaystyle z_{0}:=0} m := ∞ {\displaystyle m:=\infty }
對於每個 n = 1 , 2 , 3 , . . . {\displaystyle n=1,2,3,...}
計算 z n := f c ( z n − 1 ) {\displaystyle z_{n}:=f_{c}(z_{n-1})}
如果 | z n | < m {\displaystyle |z_{n}|<m} 設定 m := | z n | {\displaystyle m:=|z_{n}|}
使用 牛頓法 求解 w = f c ∘ n ( w ) {\displaystyle w=f_{c}^{\circ n}(w)} w ( 0 ) := z n {\displaystyle w^{(0)}:=z_{n}} n {\displaystyle n} w ( i + 1 ) := w ( i ) − f c ∘ n ( w ( i ) ) − w ( i ) f c ∘ n ′ ( w ( i ) ) − 1 {\displaystyle w^{(i+1)}:=w^{(i)}-{\frac {f_{c}^{\circ n}(w^{(i)})-w^{(i)}}{{f_{c}^{\circ n}}'(w^{(i)})-1}}}
計算迴圈的導數 λ := f c ∘ n ′ ( w ) {\displaystyle \lambda :={f_{c}^{\circ n}}'(w)}
如果 | λ | < 1 {\displaystyle |\lambda |<1} c {\displaystyle c} n {\displaystyle n}
λ {\displaystyle \lambda } w {\displaystyle w} n {\displaystyle n} 使用牛頓法是為了加速計算 w {\displaystyle w} f c {\displaystyle f_{c}} w {\displaystyle w} λ {\displaystyle \lambda } 1 {\displaystyle 1}
我沒有關於正確性的完整證明(但這並不意味著我認為它是錯誤的;這些影像看起來合理)。它依賴於圍繞給定週期的每個雙曲分量的“原子域”。
它還依賴於牛頓法得到的迴圈與迭代得到的極限迴圈相同:這對於二次曼德布羅特集是正確的,因為它只有一個有限的臨界點, 0 {\displaystyle 0} ∞ {\displaystyle \infty } https://math.stackexchange.com/a/3952801 >),這意味著最多隻能有一個吸引或拋物線迴圈。
有關 C99 實現,請參見我的部落格文章 <https://mathr.co.uk/blog/2014-11-02_practical_interior_distance_rendering.html >
心形/球體檢查
int GivePeriod ( complex double c ){
if ( cabs2 ( c ) > 4.0 ) { return 0 ;} // exterior : out of first lemniscte
if ( cabs2 ( 1.0 - csqrt ( 1.0-4.0 * c )) <= 1.0 ) { return 1 ;} // main cardioid
if ( cabs2 ( 4.0 * c + 4 ) <= 1.0 ){ return 2 ;} // period 2 component
int period = GivePeriodByIteration ( c );
if ( period < 0 ) // last chance
{
iUnknownPeriod += 1 ;
//period = m_d_box_period_do(c, 0.5, iterMax_LastIteration); // not working good
}
// period > 0 means is periodic
// period = 0 means is not periodic = exterior = escaping to infinity
// period < 0 means period not found, maybe increase global variable iterMax_Period ( see local_setup)
return period ;
}