交通運輸/交通流基礎

葡萄牙的交通擁堵

交通流是研究單個駕駛員和車輛在兩點之間移動以及他們相互之間相互作用的學科。不幸的是，研究交通流很困難，因為駕駛員行為無法百分之百確定地預測。幸運的是，駕駛員往往在合理一致的範圍內表現；因此，交通流往往具有一定的合理一致性，並且可以粗略地用數學表示。為了更好地表示交通流，已經建立了三個主要特徵之間的關係：（1）流量，（2）密度和（3）速度。這些關係有助於道路設施的規劃、設計和運營。

交通流理論

時空圖

顯示車輛隨時間和空間變化軌跡的時空圖

交通工程師用時空圖來表示特定時間特定車輛的位置。這個二維圖顯示了車輛從特定起點到特定終點的移動軌跡。該圖可以表示多輛車，因此可以確定某些特徵，例如在特定時間特定地點的流量。

流量和密度

流量 (q) = 車輛透過固定點（車輛數/小時）的速率，$t_{measured}$ = 平均測量時間間距

$q={\frac {3600N}{t_{measured}}}\,\!$

密度（濃度）(k) = 一段路段 (L) 上的車輛數 (N)（單位為車輛數/公里）

$k={\frac {N}{L}}\,\!$

其中

• $N$ = 佔用長度為 $L$ 的公路段的車輛數
• $q$ = 等效每小時流量
• $L$ = 道路長度
• $k$ = 密度

速度

測量交通速度並不像看起來那麼簡單；我們可以對一段時間或空間內單個車輛的速度測量進行平均，而每種方法都會產生略微不同的結果。

時間平均速度

時間平均速度 (${\overline {v_{t}}}\,\!$) = 透過某一點的車輛速度的算術平均值

${\overline {v_{t}}}={\frac {1}{N}}\sum \limits _{n=1}^{N}{v_{n}}\,\!$

空間平均速度

空間平均速度 (${\overline {v_{s}}}\,\!$) 被定義為一段時間內透過某一點的速度的調和平均值。它也等於一段路段上的平均速度。

${\overline {v_{s}}}={\frac {N}{\sum \limits _{n=1}^{N}{\frac {1}{v_{n}}}}}\,\!$

時間平均速度和空間平均速度的關係

請注意，時間平均速度是指透過某一點的平均速度，不同於空間平均速度，後者是指沿一段長度的平均速度。

兩種速度之間的關係如下：

${\overline {v_{t}}}={\overline {v_{s}}}+{\frac {\sigma _{s}^{2}}{\overline {v_{s}}}}\,\!$

時間平均速度高於空間平均速度，但二者之間的差異會隨著車輛速度可變性的程度而變化。在高速（自由流動）狀態下，差異很小，而在擁堵情況下，二者之間的差異可能達到兩倍。

間距

以下定義給出了所謂的brutto間隙（Asela）（義大利語，意思是“總的”），與之相對的是netto間隙（義大利語，意思是“淨的”）。Netto間隙指的是車輛後保險槓與下一輛車前保險槓之間的距離或時間。

時間間距

時間間距 ($h_{t}\,\!$) = 一輛車的車頭到達高速公路上某一點的時間與下一輛車的車頭到達同一點的時間之間的差值（以秒為單位）。

平均時間間距 (${\overline {h_{t}}}\,\!$) = 每單位距離的平均行駛時間 * 平均空間間距

${\overline {h_{t}}}={\overline {t}}*{\overline {h_{s}}}\,\!$

空間間距

空間間距 ($h_{s}$) = 一輛車的車頭與下一輛車的車頭之間的位置差（以米為單位）。

平均空間間距 (${\overline {h_{s}}}\,\!$)= 空間平均速度 * 平均時間間距

${\overline {h_{s}}}={\overline {v_{s}}}*{\overline {h_{t}}}\,\!$

請注意，密度和空間車頭間距是相關的。

$k={\frac {1}{\overline {h_{s}}}}\,\!$

交通流量的基本圖

傳統的交通流量基本圖

2000年11月1日在明尼阿波利斯第49/53大道I-94檢測器688上，流量隨密度變化

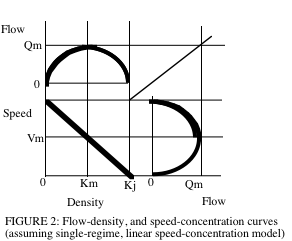
流量、密度和空間平均速度這三個變數在定義上是相關的，如

$q=k{\overline {v_{s}}}\,\!$

傳統模型（拋物線型）

傳統基本圖的屬性。

• 當高速公路上的密度為零時，流量也為零，因為高速公路上沒有車輛。
• 隨著密度的增加，流量也增加。
• 當密度達到最大擁堵密度 ($k_{j}$) 時，流量必須為零，因為車輛將首尾相連排成一行。
• 流量也會增加到最大值 ($q_{m}$)，超過該點的密度增加會導致流量減少。
• 速度是空間平均速度。
• 當密度 = 0 時，速度是自由流動速度 ($v_{f}$)。流量曲線的上半部分是不擁擠的，下半部分是擁擠的。
• 流量密度曲線的斜率表示速度。上升/下降 = 流量/密度 = 每小時車輛數/每公里車輛數 = 公里/小時。

觀察結果（三角形或截斷三角形）

實際交通資料通常比理想模型所建議的要嘈雜得多。然而，我們往往看到的是，隨著密度的增加，速度保持不變到一定程度（容量），然後如果受到下游交通的影響（排隊溢位）就開始下降。對於單個路段而言，流量和密度之間的關係因此更接近三角形而不是拋物線。當我們將多個路段彙總在一起（例如，網路）時，我們會看到更接近拋物線的形狀。

微觀模型和宏觀模型

描述交通流量的模型可以分為兩類：微觀模型和宏觀模型。理想情況下，宏觀模型是微觀模型中所見行為的集合。

微觀基本圖（截斷三角形）中的交通階段

排隊累積輸入-輸出（Newell）圖中的交通階段

微觀模型

微觀模型預測汽車的以下行為（速度和位置的變化）作為領先車輛行為的函式。

宏觀模型

宏觀交通流量理論將交通流量、行駛速度和密度聯絡起來。將交通流量比作河流，它主要是在有限通道道路上發展起來的（Leutzbach 1988）。基本關係“q=kv”（流量 (q) 等於密度 (k) 乘以速度 (v)）由基本圖說明。許多實證研究量化了組成成分的雙變數關係（q 與 v、q 與 k、k 與 v），改進引數估計和函式形式（Gerlough 和 Huber 1975、Pensaud 和 Hurdle 1991；Ross 1991；Hall、Hurdle 和 Banks 1992；Banks 1992；Gilchrist 和 Hall 1992；Disbro 和 Frame 1992）。

最常用的模型是 Greenshields 模型，它假設速度和密度之間的關係是線性的。在高效能計算機出現之前，這些模型是最合適的，當時高效能計算機使得使用微觀模型成為可能。宏觀屬性（如流量和密度）是單個（微觀）決策的產物。然而，這些微觀決策者會受到周圍環境的影響，即交通的宏觀屬性。

雖然交通流量理論家將交通流量表示為流體，但排隊分析本質上將交通流量視為一組離散粒子。這兩種表示並不一定是矛盾的。右側的圖形顯示了基本圖和排隊輸入-輸出圖中的相同 4 個階段。這將在下一節中詳細討論，請參見 下一節。

示例

示例 1：時間平均速度和空間平均速度

T問題

問題

給定五個觀察到的速度（50 公里/小時、35 公里/小時、45 公里/小時、20 公里/小時和 50 公里/小時），時間平均速度和空間平均速度是多少？

示例

解決方案

時間平均速度

${\overline {v_{t}}}={\frac {1}{5}}(60+35+45+20+50)=42\,\!$

時均速度

${\overline {v_{s}}}={\frac {N}{\sum \limits _{n=1}^{N}{\frac {1}{v_{n}}}}}={\frac {5}{{\frac {1}{60}}+{\frac {1}{35}}+{\frac {1}{45}}+{\frac {1}{20}}+{\frac {1}{50}}}}=36.37\,\!$

時均速度為 42 公里/小時，空均速度為 36.37 公里/小時。

示例 2：計算交通流量特徵

T問題

問題

已知 40 輛車在 1 分鐘內經過某一點，並行駛了 1 公里，請問流量、密度和時間間隔分別為多少？

示例

解決方案

計算流量和密度

$q={\frac {3600(40)}{60s}}=2400veh/hr\,\!$

$k={\frac {40}{1}}=40veh/km\,\!$

查詢空均速度

$q=k{\overline {v_{s}}}=2400=40{\overline {v_{s}}}\,\!$

${\overline {v_{s}}}=60km/hr\,\!$

計算空間間隔

$k=40={\frac {1}{\overline {h_{s}}}}\,\!$

${\overline {h_{s}}}=0.025km=25m\,\!$

計算時間間隔

${\overline {h_{s}}}={\overline {v_{s}}}*{\overline {h_{t}}}=25=(60*1000/3600){\overline {h_{t}}}\,\!$

${\overline {h_{t}}}=1.5s\,\!$

時間間隔為 1.5 秒。

示例 3：在某路段觀察到的點速度（單位：公里/小時）分別為 66、62、45、79、32、51、56、60、53 和 49。中位速度（單位：公里/小時）為 。

解決方案：中位速度是在一系列按升序排列的瞬時速度中位於中間值的速率。50% 的速度值將大於中位數，50% 的速度值將小於中位數。瞬時速度研究的升序排列為 32、39、45、51、53、56、60、62、66、79。

中位速度 = (53 + 56) / 2 = 54.5 公里/小時。

思考問題

問題

微觀交通流模擬單個車輛的行為，而宏觀交通流模擬整個交通流的行為。從概念上講，微觀交通流似乎更準確，因為它基於駕駛員行為而不是簡單的流量特徵。假設微觀模擬可以校準以真正解釋駕駛員行為，那麼模擬大型網路的主要缺點是什麼？

解決方案

計算能力。要使用微觀模擬來模擬非常大的網路，需要評估的車輛數量非常大，需要大量的計算機記憶體。目前，計算機在及時完成非常大的微觀網路方面存在問題，但未來可能會有所突破，從而解決這個問題。

示例問題

• 問題 (解決方案)

變數

• $d_{n}$= 第 n 輛車的距離
• $t_{n}$= 第 n 輛車的行駛時間
• $v_{n}$= 第 n 輛車的速度（速度）
• $h_{t,nm}$= 第 n 輛車和第 m 輛車之間的時間間隔
• $h_{s,nm}$ = 第 n 輛車和第 m 輛車之間的空間（距離）間隔
• $q$ = 經過固定點的流量（每小時車輛數）
• $N$ = 車輛數量
• $t_{measured}$ = 測量持續時間（秒數）
• $t$= 行駛時間
• $k$= 密度（每公里車輛數）
• $L$= 道路路段長度（公里）
• $v_{t}$= 時間平均速度
• $v_{s}$= 空間平均速度
• $v_{f}$= 自由流速度（無擁堵速度）
• $k_{j}$= 擁堵密度
• $q_{m}$= 最大流量

關鍵詞

• 時空圖
• 流量，速度，密度
• 車頭間距（空間和時間）
• 空間平均速度，時間平均速度
• 微觀，宏觀

補充閱讀

• 交通流理論修訂專著

影片

• 交通流

參考文獻

• Banks, J.H. (1991). 高速公路瓶頸處的兩種容量現象：匝道控制的基礎？交通研究記錄 1320, pp. 83–90.
• Banks, James H. (1992). “高速公路速度-流量-濃度關係：更多證據和解釋”。交通研究記錄 1225:53-60.
• Cassidy, M.J. 和 R.L. Bertini (1999) 高速公路瓶頸處的一些交通特徵。交通研究第 B 部分 第 33 卷, pp. 25–42
• Disbro, John E. 和 Frame, Michael. (1992). “交通流理論和混沌行為”。交通研究記錄. 1225: 109-115.
• Gerlough, Daniel L. 和 Huber, Matthew J. (1975). 交通流理論：TRB 特別報告 165. 交通研究委員會，華盛頓特區。
• Gilchrist, Robert S. 和 Fred L. Hall. (1992). “交通流理論變數的三維關係”。交通研究記錄. 1225:99-108.
• Hall, F.L. 和 K. Agyemang-Duah (1991). 高速公路容量下降和容量定義。交通研究記錄 1320, pp. 91–98
• Hall, Fred L.，Hurdle, V. F. 和 Banks, James H. (1992). “關於高速公路速度-流量和流量-佔用（或密度）關係的最新研究綜述”。在 TRB 第 71 屆年會上發表，華盛頓特區。
• Knoop, V.L.，Hoogendoorn, S.P. 和 Van Zuylen, H.J. (2009) 時間平均速度和空間平均速度之間的經驗差異。在 Appert-Rolland, C.，Chevoir, F.，Gondret, P.，Lassarre, S.，Lebacque, J.-P. 和 Schreckenberg, M.（編輯）交通和顆粒流 07 會議論文集。第 351-356 頁，施普林格，紐約
• Pensaud, B.N. 和 Hurdle, V. F. (1991). “一些挑戰關於速度-流量關係的舊觀念的新資料”。交通研究記錄. 1194: 191-8.
• Ross, Paul. (1991). “宏觀交通模型的一些屬性”。交通研究記錄. 1194: 129-34.