幾何課程/多邊形/三角形/直角三角形

直角三角形

直角三角形是一個有一個角等於 90^o 且另外兩個角之和等於 90^o 的三角形。

勾股定理

直角三角形的三個邊之間的關係如下所示

(斜邊)² = (鄰邊)² + (對邊)²

$b^{2}=a^{2}+c^{2}$

三角函式三角形

在直角三角形中，正弦、餘弦和正切的三角函式比可以用來求未知角和未知邊的長度。三角形的邊被稱為：

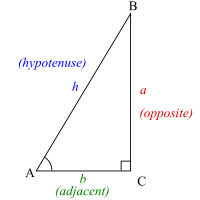
• 斜邊是對直角的邊，或定義為直角三角形的最長邊，在本例中為 h。
• 對邊是與我們感興趣的角度相對的邊，在本例中為 a。
• 鄰邊是與我們感興趣的角度和直角接觸的邊，因此得名。在本例中，鄰邊為 b。

正弦

一個角的正弦是對邊長度與斜邊長度的比值。在本例中

$\sin A={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {a}{h}}\,.$

餘弦

一個角的餘弦是鄰邊長度與斜邊長度的比值。在本例中

$\cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{h}}\,.$

正切

一個角的正切是對邊長度與鄰邊長度的比值。在本例中

$\tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}\,.$

正弦、餘弦和正切規則

一個邊長分別為 a、b 和 c，角分別為 α、β 和 γ 的三角形。

正弦定律，或正弦規則， 指出邊長與其對應對角正弦的比值是常數，即

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}.$

該比率等於給定三角形外接圓的直徑。該定理的另一種解釋是，每個角為 $\alpha$，$\beta$ 和 $\gamma$ 的三角形與邊長分別為 $\sin \alpha$，$\sin \beta$ 和 $\sin \gamma$ 的三角形相似。這個三角形可以透過首先構造一個直徑為 1 的圓，並在其中刻畫三角形的兩個角來構建。該三角形的邊長將分別為 $\sin \alpha$，$\sin \beta$ 和 $\sin \gamma$。邊長為 $\sin \alpha$ 的邊與角度為 $\alpha$ 的角相對，等等。

餘弦定理，或稱為餘弦法則，將三角形中未知邊的長度與其他邊的長度以及與未知邊相對的角連線起來。根據該定理

對於一個邊長為 $a$，$b$，$c$ 的三角形，其角度分別為 $\alpha$，$\beta$，$\gamma$，已知三角形的兩條邊長 $a$ 和 $b$，以及兩條已知邊之間的夾角 $\gamma$（或未知邊 $c$ 的對角），可以使用以下公式計算第三邊 $c$

$c^{2}\ =a^{2}+b^{2}-2ab\cos(\gamma )$

$b^{2}\ =a^{2}+c^{2}-2ac\cos(\beta )$

$a^{2}\ =b^{2}+c^{2}-2bc\cos(\alpha )$

如果已知任何三角形三條邊的長度，則可以計算三個角

$\alpha =\arccos \left({\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)$

$\beta =\arccos \left({\frac {a^{2}+c^{2}-b^{2}}{2ac}}\right)$

$\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)$

正切定理或正切法則，不如其他兩個法則知名。它指出

${\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.$

它並不常用，但可以用來在已知兩邊一角或兩角一邊的情況下求邊或角。