小學幾何/等邊三角形的作圖

引言

等邊三角形

在這一章中，我們將向你展示如何畫一個等邊三角形。什麼是“等邊”？它僅僅意味著三角形的三條邊長度相同。

任何頂點（點）為A、B和C的三角形寫作：$\triangle ABC$.

如果是等邊三角形，它將看起來像圖片中的那樣。

作圖

1. 使用你的尺子，畫一條線段，長度任意，只要是你想要的三角形的邊長即可。
   將線段的一端稱為A，另一端稱為B。
   現在你有一條名為${\overline {AB}}$的線段。
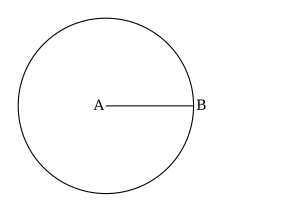
   它應該看起來像下面的圖畫。
   
2. 使用你的圓規，畫圓$\circ A,$，其圓心為A，半徑為${\overline {AB}}$。
   
3. 再次使用你的圓規畫圓$\circ B,{\overline {AB}}$，其圓心為B，半徑為${\overline {AB}}$。
   
4. 你能看到圓圈是如何相交（互相交叉）於兩點的嗎？
   這些點在下圖中用紅色顯示。
   
5. 選擇其中一個點並將其稱為C。
   我們選擇了上面的點，但如果你喜歡，也可以選擇下面的點。如果你選擇下面的點，你的三角形會看起來“倒置”，但它仍然是一個等邊三角形。
   
6. 畫一條線段，連線A和C，得到線段${\overline {AC}}$。
   
7. 畫一條線段，連線B和C，得到線段${\overline {BC}}$。
   
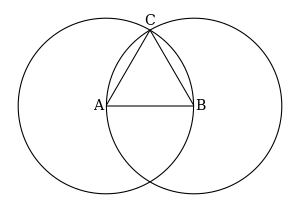
8. 三角形$\triangle ABC$的作圖已完成。

斷言

三角形$\triangle ABC$是一個等邊三角形。

證明

1. 點B和C都在圓$\circ A,{\overline {AB}}$的圓周上，點A在圓心。
   
2. 因此，線段 ${\overline {AB}}$ 與線段 ${\overline {AC}}$ 的長度相同。它們都是圓 $\circ A$ 的半徑，或者更簡單地說，${\overline {AB}}={\overline {AC}}$。
   
3. 對另一個圓我們也做同樣的事情。
   點 **A** 和 **C** 都在圓 $\circ B,{\overline {AB}}$ 的圓周上，點 **B** 位於圓心。
   
   
4. 所以我們可以說 ${\overline {AB}}={\overline {BC}}$。
   
5. 我們已經證明了 ${\overline {AB}}={\overline {AC}}$ 和 ${\overline {AB}}={\overline {BC}}$。由於 ${\overline {AC}}$ 和 ${\overline {BC}}$ 的長度都等於 ${\overline {AB}}$，它們也必須彼此相等。這可以透過替換來證明。所以我們可以說 ${\overline {AC}}={\overline {BC}}$
   
6. 因此，線段 ${\overline {AB}}$，${\overline {AC}}$ 和 ${\overline {BC}}$ 都相等。 ${\overline {AB}}={\overline {AC}}={\overline {BC}}$
   
7. 我們證明了 $\triangle ABC$ 的所有邊都相等，所以根據定義，這個三角形是等邊三角形。

證明中的問題

上面的構造簡單而優雅。可以想象孩子們用他們的腿作為圓規，偶然發現它。

然而，歐幾里得的證明是錯誤的。

在數學邏輯中，我們假設一些公理。我們透過一步一步地推進來構建證明。證明應該只由公理和可以從公理推匯出來的斷言構成。為了能夠在未來的證明中使用，一些有用的斷言被命名並稱為定理。

在歐幾里得的證明中，有一些步驟不能從公理推匯出來。例如，根據他使用的公理，圓 $\circ A,{\overline {AB}}$ 和 $\circ B,{\overline {AB}}$ 不一定相交。

雖然證明是錯誤的，但構造並不一定是錯誤的。可以透過擴充套件公理集來使構造有效。事實上，在後來的幾年裡，為了使證明有效，提出了不同的公理集。使用這些集合，用鉛筆和紙張進行的有效構造在邏輯上也是合理的。

歐幾里得，這位天才數學家，犯了這個錯誤，應該成為一個很好的例子，說明數學證明的難度以及證明和直覺之間的區別。