小學幾何/變換
變換是指我們改變圖形的大小、方向和/或位置。請注意,變換通常在方格紙上完成,以避免過多的測量並確保準確性。

反射是指圖形沿軸反射,形成一個反射對稱圖形。反射軸也是新圖形的對稱軸。
看右邊圖。假設你只被給了左邊部分。如何反射圖形?首先,找出A點和軸之間的距離。是四格。然後找到A′(讀作“A撇”),它應該與軸距離相同,但在軸的另一側。看看圖形右邊。如果你找到了那個點,你就對了。在那兒畫一個小十字 - 如果你的老師不允許你這樣做,就稍後擦掉它!現在對另外兩點做同樣的事情。把它們連線起來。現在你就形成了反射後的圖形!
反射圖形時的一個常見錯誤是忘記標記點。這會導致你損失很多分數,所以不要犯這個錯誤!此外,永遠不要錯誤地標記點。記住要新增“′”符號,並檢查點是否對應!
旋轉是最難的一種變換。它需要參考一個點旋轉圖形。因此,在這個階段,你只會要求旋轉90°、180°和270°。(360°沒有意義,但如果你真的碰巧遇到它,你非常幸運!)在旋轉圖形之前,我們需要注意三件事。
- 旋轉的度數
- 你應該順時針還是逆時針旋轉
- 旋轉中心在哪裡
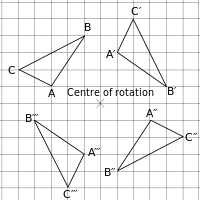
讓我們看看左邊的例子。假設我們只被給了上面的左邊部分。我們需要用不同的方法旋轉它。
- 繞中間點逆時針旋轉90°
- 繞中間點逆時針旋轉180°
- 繞中間點逆時針旋轉270°
- 繞中間點順時針旋轉90°
- 繞中間點順時針旋轉180°
- 繞中間點順時針旋轉270°
看看#1和#6。如果你仔細觀察,你會發現#1和#6實際上是一樣的!可以透過這個例子來解釋。要將三角形ABC繞中間點逆時針旋轉90°,我們可以先使用點A。點A位於旋轉中心的左邊三格,上面一格,所以我們可以將它旋轉90度。這無法用語言解釋,所以試著看看右邊圖。正如你所看到的,A和A′與旋轉中心距離相同。我們對另外兩點做同樣的事情,產生一個看起來像圖中三角形的三角形。如果我們對第6個點做同樣的事情,你將產生一個相同的三角形!第3個和第4個點也是一樣的。
那麼2和5呢?正如我們所看到的,它們都涉及旋轉180°;然而,一個是順時針,另一個是逆時針。讓我們先嚐試順時針旋轉它。你應該得到圖中的三角形A′′B′′C′′。然後對逆時針方向做同樣的事情。它們看起來一樣嗎?
既然我們已經嘗試從一個旋轉中心旋轉了6種可能性,並且發現只有三種,你能嘗試將三角形ABC繞點A旋轉嗎?如果你正在閱讀電子書,請在方格紙上覆制三角形ABC。如果你使用的是印刷版本,你可以直接在書上畫新三角形。將你的新三角形命名為DEF。
平移是一種簡單的變換。簡單來說,平移是指改變圖形的位置。例如,如果我們想將圖形向左平移五格,我們只需將它向左移動五格。
平移的過程非常簡單。假設我們在方格紙上有一個直角三角形ABC。我們的任務是將其向上平移四格,向左平移兩格。我們將直角頂點,命名為A,作為我們的點,將其向上平移四格,然後向左平移兩格。在那裡畫一個小十字,並標記為A′。現在我們參考原始圖形重新建立圖形。記住要正確命名點。
我們經常被要求追溯在給定平移中發生的平移。我們會得到原始圖形和新圖形。當處理這種型別的問題時,使用一個點可能會有所幫助,就像我們上面所做的那樣。取同一個直角三角形。我們看到A被向上平移了四格。所以我們寫道:將A向上平移四格。然後我們看到A向左平移了兩格,所以我們寫道,然後將A向左平移兩格。然後我們就完成了問題!
下表顯示了進行變換時會發生哪些變化。
| 變換型別 | 大小 | 形狀 | 方向(方向) | 位置 |
|---|---|---|---|---|
| 反射 | 從不 | 從不 | 總是 | 有時 |
| 旋轉 | 從不 | 從不 | 總是 | 有時 |
| 平移 | 從不 | 從不 | 從不 | 總是 |
| 放大(縮放) | 總是 | 從不 | 從不 | 有時 |
| 縮小(縮放) | 總是 | 從不 | 從不 | 有時 |
注意:對於所有這些變化,形狀永遠不會改變。三角形永遠是三角形,矩形永遠是矩形。
