HSC 擴充套件 1 和 2 數學/3-單元/預備/引數方程

曲線的引數形式是一種代數表示，它將曲線上的每個點的座標表示為一個引入的引數的函式，最常見的是 $t$。這與笛卡爾形式形成對比，引數方程沒有描述 $x$ 和 $y$ 之間的明確關係。必須推匯出這種關係才能從引數形式轉換為笛卡爾形式。

在 3-單元中，引數方程側重於二次函式的引數表示，從引數形式轉換為笛卡爾形式，反之亦然，並使用引數方程操作二次函式的幾何方面。識別其他引數形式也很有用，更多形式將在 4-單元主題中引入和處理，圓錐曲線.

使用引數形式的原因

在特定情況下（在學校教學大綱中，主要是 圓錐曲線），引數表示可能是有用的，因為

• 曲線上的點由一個數字而不是兩個數字表示，簡化了代數；
• 一些優雅的結果是可能的；例如，在二次函式的標準引數化中，梯度等於引數，$t$；
• 一些無法用函式形式表示的曲線（例如圓，既不是 $x$ 的函式，也不是 $y$ 的函式）可以用引數形式方便地表示；
• 從直觀上講，它提供了一種更簡單的方法來找到圖上的點：你可以代入引數的任何值，並立即找到一個點，而關係形式並非以相同的方式確定性。

此外，引數形式出現在某些自然現象中。例如，使用運動方程，可以用拋射運動定律計算丟擲球在任何時間的位置。這隱含地透過時間對球的路徑進行引數化；為了找到球路徑的形狀（我們知道它是一個拋物線），我們必須使用引數方程，從方程中消除時間，$t$。

將引數方程轉換為笛卡爾方程

最簡單的引數形式之一是直線

${\begin{aligned}x&=t\\y&=t\end{aligned}}$

透過觀察，很明顯這描述了直線 $y=x$。但是，正式執行此操作的方法是什麼？

我們正在尋找 $x$ 和 $y$ 之間的某種關係，其中沒有 $t$ 。換句話說，我們想要消去方程中的 $t$ 。在上面的例子中，我們透過將第一個和第二個方程相等來消除 $t$ 。

另一個例子

${\begin{aligned}x&=3t+1\\y&=9t^{2}-1\end{aligned}}$

我們解第一個方程得到t，並代入第二個方程

${\begin{aligned}x&=3t+1\\t&={\frac {x-1}{3}}\end{aligned}}$

代入第二個方程

${\begin{aligned}y&=9t^{2}-1\\&=9\left({\frac {x-1}{3}}\right)^{2}-1\\&=x^{2}-2x+1-1\\&=x^{2}-2x\end{aligned}}$

這裡我們得到了一個笛卡爾形式，如所要求的那樣。

三種標準引數形式

這些引數形式經常出現，三單元和四單元的學生應該認識它們。

拋物線

拋物線的標準引數化描述了一個焦距為 $a\,$ 且頂點在原點的拋物線。在笛卡爾形式中，它表示為

$x^{2}=4ay\,$

在引數形式中，它表示為

${\begin{aligned}x&=2at\\y&=at^{2}\end{aligned}}$

消去 $t\,$ 可以驗證它等效於笛卡爾形式

${\begin{aligned}x&=2at\\x^{2}&=4a^{2}t^{2}\\&=4a(at^{2})\\&=4ay\end{aligned}}$

如需。

圓

圓的圖示，指示引數的幾何意義

半徑為 $r\,$ 且圓心位於原點的圓可以用笛卡爾座標系表示為

$x^{2}+y^{2}=r^{2}\,$

引入引數 $\theta \,$，它就是

${\begin{aligned}x&=r\cos \theta \\y&=r\sin \theta \end{aligned}}$

我們轉換為笛卡爾座標系如下

${\begin{aligned}x^{2}&=r^{2}\cos ^{2}\theta \\y^{2}&=r^{2}\sin ^{2}\theta \\x^{2}+y^{2}&=r^{2}\cos ^{2}\theta +r^{2}\sin ^{2}\theta \\&=r^{2}(\cos ^{2}\theta +\sin ^{2}\theta )\end{aligned}}$

回顧三角恆等式，

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

我們得出結論

$x^{2}+y^{2}=r^{2}\,$

如需。

幾何解釋

與大多數引數方程不同，圓錐曲線由 $\theta \,$ 而不是 $t\,$ 引數化。對於圓來說，這意味著一種幾何表示：$\theta \,$ 代表該點與 $x$ 軸的夾角。

橢圓

從概念上講，橢圓只是一個“壓扁”的圓。引數形式清楚地表明瞭這一點。

${\begin{aligned}x&=a\cos \theta \\y&=b\sin \theta \end{aligned}}$

餘弦和正弦仍然存在，但現在它們被乘以了 *不同的* 常數，以便$x$ 和 $y$ 分量以不同的方式拉伸。我們可以以類似於圓形的方式將其轉換為引數形式。

${\begin{aligned}x^{2}&=a^{2}\cos ^{2}\theta \\y^{2}&=b^{2}\sin ^{2}\theta \\{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}&=\cos ^{2}\theta +\sin ^{2}\theta \\&=1\end{aligned}}$

這是橢圓的標準形式，其中 $x$ 和 $y$ 截距分別為 $\pm a\,$ 和 $\pm b\,$。

拋物線的性質

3-Unit 的學生應該記住拋物線的引數描述 ($x=2at,y=at^{2}$)。他們也應該知道（或者能夠快速推匯出）拋物線上點 $t$ 和點 $(x_{1},y_{1})$ 的切線和法線方程。

切線和法線方程的推導

對每個引數方程關於 $t\,$ 求導數，

${\begin{aligned}{\frac {dy}{dt}}&=2at\\{\frac {dx}{dt}}&=2a\end{aligned}}$

那麼，梯度 ${\tfrac {dy}{dx}}$ 可以透過將 ${\tfrac {dy}{dt}}$ 除以 ${\tfrac {dx}{dt}}$ 獲得（這是鏈式法則）。

${\begin{aligned}{\frac {dy}{dx}}&={\frac {dy}{dt}}{\frac {dt}{dx}}\\&={\frac {2at}{1}}{\frac {1}{2a}}\\&=t\end{aligned}}$

請注意，此結果無需鏈式法則即可得出，只需對笛卡爾形式（相對於 $x\,$）求導，並解出 $t\,$。然而，以上推導更快更優雅。

點 *P* 處的切線方程

拋物線的示意圖，顯示了點 *P* 處的法線和切線

點 $P(2at,at^{2})$ 處的切線的斜率為 $t$。點 $P$ 處的切線方程為

使用點斜式公式 $y-y_{1}=m(x-x_{1})\,$，方程為

${\begin{aligned}y-at^{2}&=t(x-2at)\\&=tx-2at^{2}\\y+at^{2}&=tx\\y-tx+at^{2}&=0&{\mbox{ or }}y=xt-at^{2}\end{aligned}}$

點 *P* 處的法線方程

點 $P$ 處的法線的斜率為 ${\tfrac {-1}{t}}$（因為兩條垂直線的斜率 $m_{1}\,$ 和 $m_{2}\,$ 必須滿足 $m_{1}m_{2}=-1\,$）。類似於切線方程的推導

${\begin{aligned}y-at^{2}&={\tfrac {-1}{t}}(x-2at)\\&={\tfrac {-x}{t}}+{\tfrac {2at}{t}}\\yt-at^{3}&=-x+2at\\yt+x-at(t^{2}+2)&=0&{\mbox{or }}x+ty=2at+at^{3}\end{aligned}}$

拋物線的弦

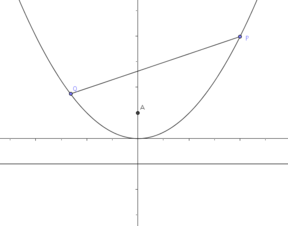拋物線和絃 PQ 的示意圖

假設$P(2ap,ap^{2})$ 和 $Q(2aq,aq^{2})$ 是拋物線 $x^{2}=4ay$ 上的兩個不同點。我們可以透過求斜率並使用點斜式來推匯出直線 $PQ$ 的方程

${\begin{aligned}m&={\frac {ap^{2}-aq^{2}}{2ap-2aq}}\\&={\frac {a(p-q)(p+q)}{2a(p-q)}}\\&={\tfrac {1}{2}}(p+q)\end{aligned}}$

所以弦為

${\begin{aligned}y-ap^{2}&={\tfrac {1}{2}}(p+q)(x-2ap)\\&={\tfrac {1}{2}}(p+q)x-ap^{2}-apq\\y&={\tfrac {1}{2}}(p+q)x-apq\end{aligned}}$

切線的交點

點 $P(2ap,ap^{2})$ 和 $Q(2aq,aq^{2})$ 位於拋物線 $x^{2}=4ay$ 上。點 $P$ 和 $Q$ 處切線的交點可以用 $p$ 和 $q$ 表示。

切線是

${\begin{aligned}y&=px-ap^{2}\\y&=qx-aq^{2}\end{aligned}}$

將兩式相減，得

${\begin{aligned}y-y&=px-ap^{2}-(qx-aq^{2})\\0&=px-ap^{2}-qx+aq^{2}\\0&=px-qx+aq^{2}-ap^{2}\\x(p-q)&=a(p^{2}-q^{2})\\x(p-q)&=a(p+q)(p-q)\\x&=a(p+q)\end{aligned}}$

將此結果代入原始的切線公式，得

${\begin{aligned}y&=p(a(p+q))-ap^{2}\\&=ap(p+q)-ap^{2}\\&=ap^{2}+apq-ap^{2}\\&=apq\end{aligned}}$

因此，交點可由 $T(a(p+q),apq)\,$ 描述。