Haskell/理解箭頭

箭頭，就像單子一樣，表達了在特定上下文中發生的計算。但是，它們比單子更抽象，因此允許使用單子類無法實現的上下文。這兩種抽象之間的本質區別可以概括為

正如我們將單子型別 m a 視為“提供 a 的計算”；我們也將箭頭型別 a b c（即引數化型別 a 對兩個引數 b 和 c 的應用）視為“具有 b 型別輸入並提供 c 的計算”；箭頭將對輸入的依賴關係明確地表示出來。

——John Hughes，將單子泛化為箭頭

本章主要分為兩部分。首先，我們將考慮箭頭計算與我們習慣的函子類所表達的計算的主要區別，並將簡要介紹一些與箭頭相關的核心型別類。其次，我們將研究 John Hughes 在箭頭最初的介紹中使用的解析器示例。

Arrow 速查指南

箭頭看起來很像函式

理解箭頭的第一步是認識到它們與函式有多相似。與 (->) 一樣，Arrow 例項的型別建構函式的種類是 * -> * -> *，也就是說，它接受兩個型別引數——不像 Monad，它只接受一個。重要的是，Arrow 以 Category 作為超類。Category 大致來說是表示可以像函式一樣組合的事物的類

class Category y where
    id  :: y a a                   -- identity for composition.
    (.) :: y b c -> y a b -> y a c -- associative composition.

函式具有 Category 的例項——事實上，它們也是 Arrow。

這種相似性的一個實際結果是，在檢視充滿 Arrow 運算子的表示式時，您必須以無點方式思考，例如 教程 中的這個示例

(total &&& (const 1 ^>> total)) >>> arr (uncurry (/))

否則，您將很快迷失在尋找應用事物的值的過程中。無論如何，即使以正確的方式檢視此類表示式，也很容易迷失方向。這就是 proc 符號的意義所在：在使某些運算子隱式的情況下新增額外的變數名稱和空格，以便 Arrow 程式碼更容易理解。

在繼續之前，我們應該提到 Control.Category 還定義了 (<<<) = (.) 和 (>>>) = flip (.)，這非常常用，用於從左到右組合箭頭。

Arrow 在 Applicative 和 Monad 之間滑動

儘管我們上面給出了警告，但箭頭可以與 applicative 函子 和 單子 相比。訣竅是使函子看起來更像箭頭，而不是相反。也就是說，您不應該將 Arrow y => y a b 與 Applicative f => f a 或 Monad m => m a 進行比較，而應該與

• Applicative f => f (a -> b)，靜態態射的型別，即 (<*>) 左側的值；以及
• Monad m => a -> m b，Kleisli態射的型別，即 (>>=) 右側的函式 。

態射是可以具有 Category 例項的，事實上我們可以為靜態態射和 Kleisli態射都編寫 Category 的例項。這種小小的扭轉足以進行合理的比較。

如果這個論證讓您想起了關於 能力滑梯 的討論，其中我們比較了 Functor、Applicative 和 Monad，那麼這是一個表明您注意到了的跡象，因為我們正在遵循完全相同的路線。在那次討論中，我們提到態射的型別限制了它們可以或不能建立的效果。單子繫結可以根據提供給 Kleisli態射的 a 值，對計算的效果進行近乎任意的更改，而 applicative 計算中函子包裝器和函式箭頭之間的隔離意味著 applicative 計算中的效果根本不依賴於函子中的值 。

從這個角度來看，箭頭與之不同之處在於，在Arrow y => y a b中，上下文y與函式箭頭之間不存在這種聯絡來嚴格確定可能性的範圍。靜態和 Kleisli 態射都可以被製成Arrow，反之，Arrow的例項也可以被製成像Applicative一樣有限，或者像Monad一樣強大。更有趣的是，我們可以使用Arrow來採取第三種選擇，在一個上下文中同時擁有類似於應用函子的靜態效果和類似於單子的動態效果，但它們彼此分離。箭頭使我們能夠微調如何組合效果。這是基於箭頭的解析器經典示例的主要推動力，我們將在本章末尾對其進行研究。

Arrow可以多工處理

這些是Arrow的方法

class Category y => Arrow y where
    -- Minimal implementation: arr and first
    arr    :: (a -> b) -> y a b                 -- converts function to arrow
    first  :: y a b -> y (a, c) (b, c)          -- maps over first component

    second :: y a b -> y (c, a) (c, b)          -- maps over second component
    (***)  :: y a c -> y b d -> y (a, b) (c, d) -- first and second combined
    (&&&)  :: y a b -> y a c -> y a (b, c)      -- (***) on a duplicated value

透過這些方法，我們可以對看起來像是線性箭頭鏈的每一步進行多個計算。這是透過將用於獨立計算的值作為（可能是巢狀的）對中的元素來保留，然後使用對處理函式在需要時訪問每個值來完成的。例如，這允許儲存中間值供以後使用，或者方便地使用具有多個引數的函式。

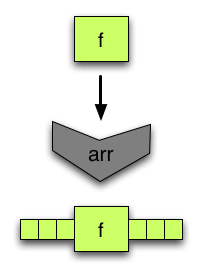
視覺化可能有助於理解箭頭計算中的資料流。以下是(>>>)和五個Arrow方法的說明

• 
  arr將函式轉換為箭頭，可以與其他箭頭組合。當然，並非所有箭頭都是以這種方式建立的。
• 
  (>>>)組合兩個箭頭。第一個箭頭的輸出被饋送到第二個箭頭。
• 
  first並排接受兩個輸入。第一個使用箭頭進行修改，而第二個保持不變。
• 
  相反，second接受兩個輸入，但只修改第二個。
• 
  (***)接受兩個輸入，並使用兩個箭頭對它們進行修改，每個輸入一個箭頭。
• 
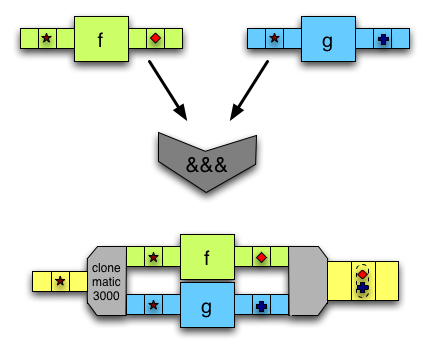
  (&&&)接受一個輸入，將其複製，並使用不同的箭頭修改每個副本。

來自教程的mean1箭頭的資料流。矩形是箭頭，圓角矩形是使用arr建立的箭頭，圓圈是其他資料流拆分/合併點。其他組合器被隱含。對應程式碼

(total &&& (const 1 ^>> total))
    >>> arr (uncurry (/))

值得一提的是，Control.Arrow 將returnA = arr id 定義為一個不執行任何操作的箭頭。箭頭定律之一指出returnA必須等效於Category例項中的id。

ArrowChoice可以是堅決的

如果Arrow使多工處理成為可能，那麼ArrowChoice會強制執行對要執行的任務的決策。

class Arrow y => ArrowChoice y where
    -- Minimal implementation: left
    left  :: y a b -> y (Either a c) (Either b c)          -- maps over left choice

    right :: y a b -> y (Either c a) (Either c b)          -- maps over right choice
    (+++) :: y a c -> y b d -> y (Either a b) (Either c d) -- left and right combined
    (|||) :: y a c -> y b c -> y (Either a b) c            -- (+++), then merge results

Either提供了一種對值進行標記的方法，以便不同的箭頭可以根據它們是否用Left或Right進行標記來處理它們。請注意，這些涉及Either的方法與Arrow提供的涉及對的方法完全類似。

來自教程的getWord示例片段中的資料流。藍色表示Left標記，紅色表示Right標記。請注意，proc表示法的if結構將True傳送到Left，將False傳送到Right。對應程式碼

proc () -> do
  firstTime <- oneShot -< ()
  mPicked <- if firstTime
    then do
      picked <- pickWord rng -< ()
      returnA -< Just picked
    else returnA -< Nothing
  accum' Nothing mplus -< mPicked

ArrowApply只是無聊的

顧名思義，ArrowApply使我們能夠在箭頭計算過程中直接將箭頭應用於值。普通的Arrow不允許這樣做——我們只能不停地組合它們。應用只發生在最後，一旦使用某種執行箭頭函式從箭頭中獲得一個普通函式。

class Arrow y => ArrowApply y where
    app :: y (y a b, a) b -- applies first component to second

（例如，函式的app是uncurry ($) = \(f, x) -> f x。）

然而，app需要付出高昂的代價。將箭頭作為箭頭計算中的值構建，然後透過應用消除它，這意味著允許計算中的值影響上下文。這聽起來很像單子繫結所做的事情。事實證明，只要遵循ArrowApply定律，ArrowApply就完全等效於某些Monad。最終的結果是，ArrowApply箭頭無法實現Arrow允許但Monad不允許的任何有趣可能性，例如具有部分靜態上下文。

箭頭真正的靈活之處在於那些不是單子的箭頭，否則它就只是一個更笨拙的語法。

——菲利帕·考德羅伊

箭頭組合器出現在意想不到的地方

函式是箭頭的瑣碎示例，因此上面顯示的所有Control.Arrow函式都可以與它們一起使用。因此，在與箭頭無關的程式碼中看到箭頭組合器是很常見的。以下是它們對普通函式的作用的總結，以及其他模組中可以以相同方式使用的組合器（如果您更喜歡備選名稱，或者只是更喜歡對簡單任務使用簡單模組）。

組合器	它做什麼 （專門用於(->)）	備選方案
(>>>)	flip (.)
first	\f (x, y) -> (f x, y)	first (Data.Bifunctor)
second	\f (x, y) -> (x, f y)	fmap; second (Data.Bifunctor)
(***)	\f g (x, y) -> (f x, g y)	bimap (Data.Bifunctor)
(&&&)	\f g x -> (f x, g x)	liftA2 (,) (Control.Applicative)
left	對映到Left情況。	first (Data.Bifunctor)
right	對映到Right情況。	fmap; second (Data.Bifunctor)
(+++)	對映到兩種情況。	bimap (Data.Bifunctor)
(|||)	消除Either。	either (Data.Either)
app	\(f, x) -> f x	uncurry ($)

Data.Bifunctor模組提供了Bifunctor類，對和Either是它的例項。Bifunctor非常類似於Functor，只是有兩個獨立的方法可以將函式對映到它，分別對應於first和second方法。

練習
編寫second、(***)和(&&&)的實現。只使用(>>>)、arr和first（加上任何普通函式）來實現second；之後，一旦您實現了它們，就可以使用其他組合器。 編寫right的實現，用left表示。 實現liftY2 :: Arrow y => ‌(a -> b -> c) -> y r a -> y r b -> y r c

使用箭頭

避免洩漏

箭頭最初是由 Swierstra 和 Duponcheel發現的一種高效解析器設計所驅動。為了有一個參考點來討論其設計的好處，讓我們快速看一下單子解析器是如何工作的。

這是一個非常簡陋的單子解析器型別的說明

newtype Parser s a = Parser { runParser :: [s] -> Maybe (a, [s]) }

Parser是一個函式，它接受一個輸入流（此處為[s]型別的列表），並且根據它在輸入中找到的內容，返回一個結果（[a]型別）和一個流（通常是輸入流減去解析器消耗的一些輸入），或者Nothing。當我們說解析器成功或失敗時，我們指的是它是否產生了結果。雖然現實世界中的解析器型別，如來自 Parsec 的ParsecT，為了提供各種其他功能（尤其是失敗時的資訊性錯誤訊息）可以複雜得多，但這個簡單的Parser對於我們目前的用途已經足夠了。

例如，這是一個字串中單個字元的解析器

char :: Char -> Parser Char Char
char c = Parser $ \input -> case input of
    [] -> Nothing
    x : xs -> if x == c then Just (c, xs) else Nothing

如果輸入字串中的第一個字元是c，則char c成功，消耗第一個字元並給出c作為結果；否則，它失敗

GHCi> runParser (char 'H') "Hello"
Just ('H',"ello")
GHCi> runParser (char 'G') "Hello"
Nothing

再次看一下Parser型別，它本質上是Maybe上的State [s]。因此，我們能夠將其製成Applicative、Monad、Alternative等等的例項並不奇怪（您可能想嘗試一下）。這給了我們一套非常靈活的組合器，用於從更簡單的解析器構建更復雜的解析器。解析器可以按順序執行...

isHel :: Parser Char ()
isHel = char 'H' *> char 'e' *> char 'l' *> pure ()

... 將它們的結果組合起來...

string :: String -> Parser Char String
string = traverse char

... 或者作為彼此的備選方案進行嘗試

solfege :: Parser Char String
solfege = string "Do" <|> string "Re" <|> string "Mi"

透過最後一個例子，我們可以指出 Swierstra 和 Duponcheel 試圖解決的問題。當 solfege 在字串 "Fa" 上執行時，我們無法檢測到解析器會失敗，直到所有三個備選方案都失敗。如果我們有更復雜的解析器，其中一個備選方案可能只有在嘗試使用大量輸入流後才會失敗，那麼我們就必須以同樣的方式沿著解析器鏈向下遍歷。所有可能被後面的解析器使用的輸入都必須保留在記憶體中，以防其中一個解析器能夠使用它。這會導致比你想象的更多空間使用——這種情況通常被稱為“空間洩漏”。

可以做得更好嗎？

Swierstra 和 Duponcheel（1996）注意到，在處理某些型別的解析任務時，一個更智慧的解析器可以立即在看到第一個字元時失敗。例如，在上面的 solfege 解析器中，第一個字母解析器的選擇僅限於字母 'D'、'R' 和 'M'，分別代表 "Do"、"Re" 和 "Mi"。這個更智慧的解析器還能夠更快地進行垃圾回收，因為它可以向前檢視其他解析器是否能夠使用該輸入，並丟棄無法使用的輸入。這個新的解析器很像單子解析器，主要區別在於它匯出了“靜態”資訊。它就像一個單子，但它也會告訴你它可以解析什麼。

有一個主要問題。這與 Monad 介面不符。單子組合適用於 (a -> m b) 函式，以及函式本身。沒有辦法附加靜態資訊。你只有一個選擇，輸入一些內容，然後看看它是否透過或失敗。

當時這個問題剛出現時，單子介面被宣稱為函數語言程式設計社群中一個完全通用的工具，因此發現有一些特別有用的程式碼無法適應該介面，這是一個挫折。這就是箭頭出現的地方。John Hughes 的“將單子泛化為箭頭”提出了箭頭抽象作為一種新的、更靈活的工具。

靜態和動態解析器

讓我們從 Hughes 提出的箭頭的角度，更詳細地檢查一下 Swierstra 和 Duponcheel 的解析器。解析器有兩個部分：一個快速的靜態解析器，它告訴我們輸入是否值得嘗試解析；以及一個緩慢的動態解析器，它完成實際的解析工作。

import Control.Arrow
import qualified Control.Category as Cat
import Data.List (union)

data Parser s a b = P (StaticParser s) (DynamicParser s a b)
data StaticParser s = SP Bool [s]
newtype DynamicParser s a b = DP ((a, [s]) -> (b, [s]))

靜態解析器由一個標誌組成，該標誌告訴我們解析器是否可以接受空輸入，以及可能的“起始字元”列表。例如，單個字元的靜態解析器如下所示

spCharA :: Char -> StaticParser Char
spCharA c = SP False [c]

它不接受空字串（False），可能的起始字元列表僅包含 c。

動態解析器需要更多剖析。我們看到的是一個從 (a, [s]) 到 (b, [s]) 的函式。從兩個解析器的順序的角度思考是有用的：每個解析器都使用前一個解析器的結果（a）以及輸入流的剩餘部分（[s]），對 a 做一些操作以生成自己的結果 b，使用一些字串並返回“它”。因此，作為一個實際操作的例子，考慮一個動態解析器 (Int, String) -> (Int, String)，其中 Int 表示到目前為止解析的字元數。下表顯示瞭如果我們將幾個解析器組合在一起並在字串“cake”上執行它們會發生什麼。

	結果	剩餘部分
之前	0	cake
第一個解析器之後	1	ake
第二個解析器之後	2	ke
第三個解析器之後	3	e

因此，這裡要說明的是，動態解析器有兩個任務：對前一個解析器的輸出做一些操作（非正式地，a -> b），以及使用一部分輸入字串（非正式地，[s] -> [s]），因此型別為 DP ((a,[s]) -> (b,[s]))。現在，對於單個字元的動態解析器（型別為 (Char, String) -> (Char, String)），第一個任務是微不足道的。我們忽略前一個解析器的輸出，返回我們解析的字元，並從流中使用一個字元

dpCharA :: Char -> DynamicParser Char a Char
dpCharA c = DP (\(_,_:xs) -> (c,xs))

這可能會讓你提出一些問題。例如，如果我們只是要忽略前一個解析器的輸出，那麼接受它有什麼意義呢？而且動態解析器不應該是透過測試 x == c 來確保當前流中的字元與要解析的字元匹配嗎？第二個問題的答案是否定的——事實上，這是重點的一部分：這項工作並不必要，因為檢查已經由靜態解析器執行。當然，事情之所以如此簡單，是因為我們只測試了一個字元。如果我們要編寫一個解析多個字元的解析器，我們就需要實際測試第二個及後續字元的動態解析器；如果我們要透過連結多個字元解析器來構建一個輸出字串，那麼我們就需要前一個解析器的輸出。

現在將兩個解析器組合在一起。這是我們針對單個字元的 S+D 風格的解析器

charA :: Char -> Parser Char a Char
charA c = P (SP False [c]) (DP (\(_,_:xs) -> (c,xs)))

為了實際使用解析器，我們需要一個 runParser 函式，該函式執行靜態測試並將動態解析器應用於輸入

-- The Eq constraint on s is needed so that we can use elem.
runParser :: Eq s => Parser s a b -> a -> [s] -> Maybe (b, [s])
runParser (P (SP emp _) (DP p)) a []
    | emp = Just (p (a, []))
    | otherwise = Nothing
runParser (P (SP _ start) (DP p)) a input@(x:_)
    | x `elem` start = Just (p (a, input))
    | otherwise = Nothing

請注意，runParser 如何輸出一個型別為 [s] -> Maybe (b, [s]) 函式的函式，這本質上與我們之前演示的單子解析器相同。現在我們可以像之前使用 char 一樣使用 charA。（主要區別在於作為啞引數傳遞的 ()。這在這裡是有意義的，因為 charA 實際上不使用型別為 a 的初始值。但是，對於其他解析器，情況可能並非如此。）

GHCi> runParser (charA 'D') () "Do"
Just ('D',"o")
GHCi> runParser (charA 'D') () "Re"
Nothing

引入箭頭組合器

完成初步的介紹之後，我們現在將為 Parser s 實現 Arrow 類，並透過這樣做，讓你瞭解箭頭為何有用。所以讓我們開始吧

instance Eq s => Arrow (Parser s) where

arr 應該將任意函式轉換為解析箭頭。在這種情況下，我們必須以非常寬鬆的意義來使用“解析”：生成的箭頭接受空字串，並且只接受空字串（它的第一個字元集為 []）。它的唯一作用是獲取前一個解析箭頭的輸出並對其進行操作。因此，它不會使用任何輸入。

    arr f = P (SP True []) (DP (\(b,s) -> (f b,s)))

同樣，first 組合器也比較簡單。給定一個解析器，我們想要生成一個新的解析器，它接受一對輸入 (b,d)。輸入的第一個部分 b 是我們實際要解析的內容。第二部分保持原樣傳遞

    first (P sp (DP p)) = P sp (DP (\((b,d),s) ->
        let (c, s') = p (b,s)
        in  ((c,d),s')))

我們還需要提供 Category 例項。id 非常明顯，因為 id = arr id 必須成立

instance Eq s => Cat.Category (Parser s) where
    id = P (SP True []) (DP (\(b,s) -> (b,s)))
    -- Or simply: id = P (SP True []) (DP id)

另一方面，(.) 的實現需要更多思考。我們想要獲取兩個解析器，並返回一個組合的解析器，其中包含兩個引數的靜態解析器和動態解析器

    -- The Eq s constraint is needed for using union here.
    (P (SP empty1 start1) (DP p1)) .
      (P (SP empty2 start2) (DP p2)) =
        P (SP (empty1 && empty2)
              (if not empty1 then start1 else start1 `union` start2))
          (DP (p2.p1))

組合動態解析器很簡單；我們只需進行函式組合即可。將靜態解析器組合在一起需要一些思考。首先，組合的解析器只有在“兩個”解析器都接受空字串的情況下才能接受空字串。很公平，現在如何處理起始符號？好吧，解析器應該是按順序排列的，所以第二個解析器的起始符號實際上並不重要。如果一切都很簡單，組合解析器的起始符號將只是 start1。唉，現實並非如此簡單，因為解析器很可能會接受空輸入。如果第一個解析器接受空輸入，那麼我們就必須透過接受第一個和第二個解析器的起始符號來考慮這種情況

那麼，箭頭帶給我們什麼呢？

如果你回顧我們的 Parser 型別並清空靜態解析器部分，你可能會注意到這很像函式的箭頭例項。

arr f = \(b, s) -> (f b, s)
first p = \((b, d), s) ->
            let (c, s') = p (b, s)
            in  ((c, d), s'))

id = id
p2 . p1 = p2 . p1

有一個奇怪的 s 變數在其中，這使得定義看起來有些奇怪，但例如 簡單的 first 函式 的輪廓就在那裡。實際上，你在這裡看到的是 State 單子/Kleisli 態射的箭頭例項（讓 f :: b -> c、p :: b -> State s c 以及 (.) 實際上是 (<=<) = flip (>=>)）。

這很好，但我們可以很容易地在經典的單子風格中使用 bind 來做到這一點，將 first 變為一個奇特的輔助函式，可以用一些模式匹配輕鬆地編寫。但請記住，我們的 Parser 型別不僅僅是動態解析器——它還包含靜態解析器。

arr f = SP True []
first sp = sp
(SP empty1 start1) >>> (SP empty2 start2) = (SP (empty1 && empty2)
        (if not empty1 then start1 else start1 `union` start2))

這根本不是一個函式，它只是在操作一些資料型別，而且無法用單子形式表達。但 Arrow 介面也能很好地處理它。當我們將兩種型別結合在一起時，我們得到了兩全其美的結果：靜態解析器資料結構與動態解析器一起使用。Arrow 介面使我們能夠以透明的方式將兩個解析器（靜態和動態）組合在一起並作為單元進行操作，然後我們可以將其作為一個傳統的統一函式執行。

Arrows 在實踐中的應用

一些使用箭頭庫的例子

• Opaleye (庫文件)，一個用於 SQL 生成的庫。
• Haskell XML 工具箱 (專案頁面 和 庫文件) 使用箭頭處理 XML。Haskell Wiki 上有一個頁面，其中包含一個較為友好的 HXT 簡介。
• Netwire (庫文件) 是一個用於 函式式反應式程式設計 (FRP) 的庫。FRP 是一個用於處理事件和隨時間變化的值的函式式正規化，其用例包括使用者介面、模擬和遊戲。Netwire 既有箭頭介面，也有 applicative 介面。
• Yampa (Haskell Wiki 頁面 庫文件) 是另一個基於箭頭的 FRP 庫，是 Netwire 的前身。
• Hughes 的箭頭風格解析器最初是在他的 2000 年論文中描述的，但直到 2005 年 5 月 Einar Karttunen 釋出了 PArrows，才有了可用的實現。

參見

• 關於箭頭的參考書目（haskell.org）

鳴謝

本模組使用來自 Shae Erisson 編寫的 箭頭入門 中的文字，最初為 The Monad.Reader 4 編寫。