Haskell/Zippers

忒修斯與拉鍊

迷宮

"忒修斯，我們必須做點什麼"，古希臘公司首席營銷官荷馬說。忒修斯將米諾陶洛斯™動作模型放回架子上，點了點頭。"現在的孩子們不再對古老的神話感興趣，他們更喜歡現代英雄，比如蜘蛛俠或海綿寶寶。"英雄。忒修斯很清楚，當年在克里特島的迷宮裡，他是多麼的英雄。但那些"現代英雄"甚至沒有試圖表現得真實。是什麼讓他們如此成功？無論如何，如果即將到來的銷售問題無法解決，股東肯定會為古希臘公司安排一條通往冥河的通道。

"尤里卡！忒修斯，我有一個主意：我們把你的故事與米諾陶洛斯的故事做成電腦遊戲！你認為怎麼樣？" 荷馬是對的。已經出版了幾本書，史詩般的（而且打破排行榜的）歌曲，一部必看的電影三部曲，以及無數的忒修斯與米諾陶洛斯™小玩意，但就是沒有電腦遊戲。"完美，那就這樣吧。現在，忒修斯，你的任務是實現這個遊戲"。

作為一個真正的英雄，忒修斯選擇 Haskell 作為語言來實現公司東山再起的產品。當然，探索米諾陶洛斯的迷宮將成為遊戲的一大亮點。他沉思道："我們有一個二維迷宮，它的走廊可以指向多個方向。當然，我們可以從詳細的長度和角度抽象出來：為了找到出路，我們只需要知道路徑是如何分叉的。為了簡化，我們將迷宮建模為一棵樹。這樣，在深入行走時，分叉的兩支就無法再次連線，玩家也無法走回原路。但我認為迷路的機會已經足夠了；這樣，如果玩家足夠耐心，他們就可以用左手法則探索整個迷宮。"

data Node a = DeadEnd a
            | Passage a (Node a)
            | Fork    a (Node a) (Node a)

一個示例迷宮及其樹狀表示。

忒修斯讓迷宮的節點攜帶一個額外的型別為 a 的引數。稍後，它可能會包含遊戲相關資訊，比如節點所指地點的座標、周圍的環境、地板上的遊戲物品列表或在該迷宮區域遊蕩的怪物列表。我們假設有兩個輔助函式

get :: Node a -> a
put :: a -> Node a -> Node a

檢索和更改儲存在 Node a 每個建構函式的第一個引數中的型別為 a 的值。

練習
實現 get 和 put。get 的一個情況是 get (Passage x _) = x. 為了得到一個具體的例子，將圖片中顯示的迷宮寫成型別為 Node (Int,Int) 的值。額外的引數 (Int,Int) 持有一個節點的笛卡爾座標。

"嗯，如何表示玩家在迷宮中的當前位置？玩家可以透過選擇左右分支來探索更深的地方，就像在"

 turnRight :: Node a -> Maybe (Node a)
 turnRight (Fork _ l r) = Just r
 turnRight _            = Nothing

"但用這種方式將當前迷宮的頂部替換為相應的子迷宮是不可能的，因為這樣玩家就無法返回。"他沉思道。"啊，我們可以應用阿里阿德涅的線繩技巧來返回。我們只需要用玩家線繩經過的分支列表來表示玩家的位置，迷宮始終保持不變。"

data Branch = KeepStraightOn
            | TurnLeft
            | TurnRight
type Thread = [Branch]

用阿里阿德涅的線繩表示玩家的位置。

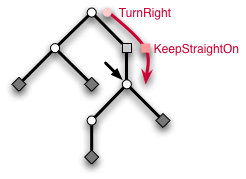
"例如，一條線繩 [TurnRight,KeepStraightOn] 表示玩家在入口處選擇了右邊的分支，然後直走了一條 Passage 來到達他們當前的位置。有了線繩，玩家現在可以透過延長或縮短線繩來探索迷宮。例如，函式 turnRight 透過將 TurnRight 附加到線繩上來延長線繩。"

turnRight :: Thread -> Thread
turnRight t = t ++ [TurnRight]

"要訪問額外的資料，即遊戲相關物品等等，我們只需要沿著線繩進入迷宮即可。"

retrieve :: Thread -> Node a -> a
retrieve []                  n             = get n
retrieve (KeepStraightOn:bs) (Passage _ n) = retrieve bs n
retrieve (TurnLeft      :bs) (Fork _ l r)  = retrieve bs l
retrieve (TurnRight     :bs) (Fork _ l r)  = retrieve bs r

練習
編寫一個函式 update，它將型別為 a -> a 的函式應用於玩家位置的額外資料。

忒修斯對這種解決方案的滿意並沒有持續很久。"不幸的是，如果我們要延長路徑或後退一步，我們必須更改列表的最後一個元素。我們可以將列表儲存為反向，但即使這樣，我們也必須反覆沿著線繩走來訪問玩家位置的迷宮中的資料。這兩個操作都需要與線繩長度成正比的時間，對於大型迷宮來說，這將花費太長時間。有沒有其他辦法？"

阿里阿德涅的拉鍊

雖然忒修斯是一位技藝高超的戰士，但他並沒有在程式設計方面進行太多訓練，也無法找到一個令人滿意的解決方案。經過了激烈的但無果的思考後，他決定打電話給他的前愛人阿里阿德涅，向她尋求建議。畢竟，是她想出了線繩的主意。
"阿里阿德涅諮詢。我能為您做什麼？"
我們的英雄立刻認出了這個聲音。
"你好阿里阿德涅，我是忒修斯。"
一陣令人不安的沉默暫停了對話。忒修斯清楚地記得，他曾在納克索斯島上拋棄了她，他知道她不會喜歡他的電話。但古希臘公司正走在通往冥府的道路上，他沒有選擇。
"嗯，親愛的，... 你好嗎？"
阿里阿德涅冷冷地反駁道：" 忒修斯先生，親愛的的日子早就過去了。你想幹什麼？"
"嗯，我，呃……我需要一些關於程式設計問題的幫助。我正在程式設計一個新的忒修斯與米諾陶洛斯™電腦遊戲。"
她嘲諷道，"又是為了美化你‘英勇存在’的另一件文物？你還想讓我幫你？"
"阿里阿德涅，求求你了，古代極客公司正瀕臨破產。這款遊戲是我們最後的希望！"
停頓了一會兒，她做出了決定。
"好吧，我會幫你。但你必須把古代極客公司的大部分股份轉讓給我。比如百分之三十。 "
忒修斯臉色蒼白。但他又能怎麼辦呢？情況已經糟糕到無法挽回的地步，於是他同意了，但只在將阿里阿德涅的股份比例降至十分之一後才同意。

忒修斯告訴阿里阿德涅他心目中的迷宮表示後，她立即給出建議，
"你需要一個拉鍊。 "
"什麼？這問題和我的拉鍊有什麼關係？"
"沒什麼，它是一個由熱拉爾·惠特首次釋出的資料結構。 "
"哦。"
"更準確地說，它是一種純粹的函式式方法，用於用一個焦點或指標增強樹形資料結構（如列表或二叉樹），該指標指向資料結構內部的子樹，並允許在它所指的位置進行恆定時間更新和查詢。在我們的案例中，我們希望玩家的位置處於焦點。 "
"我知道我自己想要快速更新，但我該怎麼編寫程式碼呢？"
"不要著急，你不能透過編碼解決問題，你只能透過思考來解決問題。在純粹的函式式資料結構中，我們能獲得恆定時間更新的唯一位置是頂層節點。因此，焦點必須始終在頂部。目前，你迷宮中的頂層節點始終是入口，但你之前將迷宮替換為其子迷宮的想法確保了玩家的位置始終在頂層節點。 "
"但問題是，如何返回，因為所有那些玩家沒有選擇分支進入的子迷宮都丟失了。"
"你可以使用我的線，這樣就不會丟失子迷宮。 "
阿里阿德涅享受著忒修斯的困惑，但在他抱怨已經用過她的線之前，她迅速繼續說道，
"關鍵是將丟失的子迷宮貼上到線上，這樣它們實際上就不會丟失。目的是讓線和當前的子迷宮互相補充形成整個迷宮。‘當前’子迷宮是指玩家所處位置的迷宮。拉鍊僅僅由線和當前的子迷宮組成。 "

type Zipper a = (Thread a, Node a)

拉鍊是阿里阿德涅的線和玩家所處位置的當前子迷宮的配對。主線是紅色的，並有子迷宮連線到它，因此整個迷宮可以從配對中重建。

忒修斯什麼也沒說。
"你也可以將線視為上下文，當前的子迷宮就位於該上下文中。現在，讓我們找出如何定義Thread a。順便說一下，Thread必須接受額外的引數a，因為它現在儲存了子迷宮。線仍然是一個簡單的分支列表，但分支與以前不同。 "

data Branch a  = KeepStraightOn a
               | TurnLeft  a (Node a)
               | TurnRight a (Node a)
type Thread a  = [Branch a]

"最重要的是，TurnLeft和TurnRight都有一個子迷宮貼上到它們上面。當玩家選擇比如向右轉時，我們用一個TurnRight擴充套件線，並將未選擇的左分支附加到它上面，這樣就不會丟失它。 "
忒修斯打斷道："等等，我該如何將此行為實現為一個函式turnRight？TurnRight的第一個引數a型別是什麼？啊，我明白了。我們不僅需要貼上會丟失的分支，還需要貼上Fork的額外資料，因為否則也會丟失。所以，我們可以透過一個初步的"來生成一個新的分支

branchRight (Fork x l r) = TurnRight x l

"現在，我們必須以某種方式用它來擴充套件現有的線。"
"確實。關於線的第二個要點是，它是反向儲存的。要擴充套件它，你需要在列表前面新增一個新的分支。要返回，你需要刪除最頂層的元素。 "
"啊哈，這使得擴充套件和返回只需要花費恆定時間，而不是像我之前的版本那樣花費與長度成正比的時間。所以turnRight的最終版本是"

turnRight :: Zipper a -> Maybe (Zipper a)
turnRight (t, Fork x l r) = Just (TurnRight x l : t, r)
turnRight _               = Nothing

從入口處獲取右子樹。當然，線最初是空的。請注意，線是反向執行的，即最頂層的段是最新的段。

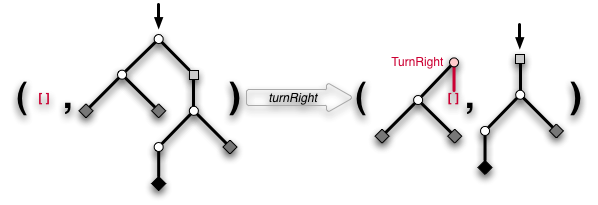
"這並不難。那麼，讓我們繼續keepStraightOn，用於向下走過通道。這比選擇分支更容易，因為我們只需要保留額外的資料："

keepStraightOn :: Zipper a -> Maybe (Zipper a)
keepStraightOn (t, Passage x n) = Just (KeepStraightOn x : t, n)
keepStraightOn _                = Nothing

現在向下走過通道。

練習
編寫函式turnLeft。

他高興地說："但有趣的部分是返回，當然。讓我們看看……"

back :: Zipper a -> Maybe (Zipper a)
back ([]                   , _) = Nothing
back (KeepStraightOn x : t , n) = Just (t, Passage x n)
back (TurnLeft  x r    : t , l) = Just (t, Fork x l r)
back (TurnRight x l    : t , r) = Just (t, Fork x l r)

"如果線是空的，我們就已在迷宮的入口處，無法返回。在所有其他情況下，我們必須繞線。由於附加到線上的元素，我們實際上可以重建我們來自的子迷宮。"
阿里阿德涅評論道，"請注意，一個部分正確性測試是檢查每個繫結變數（如x、l和r）在等號左側是否只出現一次，在等號右側也只出現一次。所以，當上下移動拉鍊時，我們只是在線和當前子迷宮之間重新分配資料。 "

練習
現在我們可以導航拉鍊了，編寫函式get、put和update，這些函式對玩家位置的額外資料進行操作。 拉鍊絕不侷限於具體的例子Node a，它們可以為所有樹形資料型別構建。繼續構建一個用於二叉樹的拉鍊 data Tree a = Leaf a | Bin (Tree a) (Tree a) 首先考慮線可以採取的可能分支Branch a。探索樹時，你需要將什麼貼上到線上？ 簡單的列表也有拉鍊。 data List a = Empty | Cons a (List a) 它看起來像什麼？ 編寫一個基於忒修斯迷宮的完整遊戲。

尤里卡！這就是忒修斯想要的解決方案，古代極客公司應該會成功，即使部分出售給了阿里阿德涅諮詢公司。但還有一個問題
"為什麼它被稱為拉鍊？"
"嗯，我會稱它為‘阿里阿德涅的珍珠項鍊’。但最有可能的是，它被稱為拉鍊，是因為線類似於拉鍊的開口部分，而子迷宮類似於拉鍊的閉合部分。在資料結構中移動類似於拉開或合上拉鍊。 "
"‘阿里阿德涅的珍珠項鍊’，”他輕蔑地說。“就好像你的線在克里特島上幫過什麼忙一樣。”
"就好像線的想法是你的，”她回答道。 "
"呸，我不需要線，”他否認了實際上確實需要線來程式設計遊戲的事實。
令他驚訝的是，她同意了，"嗯，你確實不需要線。另一個觀點是，用你的手指抓住樹的焦點，將其舉到空中。焦點將位於頂部，樹的所有其他分支都垂下來。你只需要將得到的樹分配一個合適代數資料型別，最可能的是拉鍊的型別。 "

用你的手指抓住焦點，將其舉到空中，垂下的分支將形成一個新的樹，你的手指位於頂部，準備透過一個代數資料型別進行結構化。

"哦。”他不需要阿里阿德涅的線，但他需要阿里阿德涅告訴他？這太過了。
"謝謝你，阿里阿德涅，再見。"
他看不見她，所以她並沒有掩飾她狡黠的微笑。

練習
取一個列表，用你的手指固定中間的一個元素，然後將列表舉到空中。你可以給得到的樹賦予什麼型別？

半年後，忒修斯停在一家商店的櫥窗前，無視試圖從他扣緊的夾克下鑽進來的冰冷雨水。閃爍的字母宣告道

"蜘蛛俠：迷失在網路中"

- 線上的迷宮中找到你的出路 -
古代極客公司出品的偉大電腦遊戲

他詛咒自己打電話給阿里阿德涅並將公司的一部分賣給了她那天。是她在策劃由阿里阿德涅的丈夫狄俄尼索斯領導的WineOS公司的不友好收購嗎？忒修斯看著雨滴沿著玻璃窗流下來。在生產線改變之後，再也沒有人會生產忒修斯與米諾陶洛斯™商品了。他嘆了口氣。他的時代，英雄的時代，結束了。現在是超級英雄的時代了。

資料型別的區分

上一節介紹了拉鍊，一種用指標增強樹形資料結構Node a的方法，該指標可以聚焦於不同的子樹。雖然我們為特定的資料結構Node a構建了一個拉鍊，但可以透過手動方式輕鬆地將構建方法調整到不同的樹形資料結構。

練習
從三叉樹開始 data Tree a = Leaf a | Node (Tree a) (Tree a) (Tree a) 並推匯出相應的Thread a和Zipper a。

機械微分

但也有一個完全機械的方式來推匯出任何（適當規則的）資料型別的拉鍊。令人驚訝的是，“推導”必須從字面上理解，因為拉鍊可以透過資料型別的導數獲得，這是科諾爾·麥克布萊德首次描述的發現。下一節將闡述這顆真正奇妙的數學寶石。

為了進行系統性構建，我們需要用型別進行計算。型別結構化計算的基礎知識在單獨的章節泛型程式設計中概述，我們將嚴重依賴這些材料。

讓我們看一些例子，看看它們的拉鍊有什麼共同點以及它們如何暗示差異。二叉樹的型別是遞迴方程的固定點

${\mathit {Tree2}}=1+{\mathit {Tree2}}\times {\mathit {Tree2}}$.

當沿著樹向下走時，我們迭代地選擇進入左子樹或右子樹，然後將未進入的子樹貼上到阿里阿德涅的線。因此，我們線的分支型別為

${\mathit {Branch2}}={\mathit {Tree2}}+{\mathit {Tree2}}\cong 2\times {\mathit {Tree2}}$.

類似地，三叉樹的線

${\mathit {Tree3}}=1+{\mathit {Tree3}}\times {\mathit {Tree3}}\times {\mathit {Tree3}}$

具有型別為

${\mathit {Branch3}}=3\times {\mathit {Tree3}}\times {\mathit {Tree3}}$

因為在每一步，我們可以在三個子樹之間選擇，並且必須儲存我們沒有進入的兩個子樹。這與導數${\frac {d}{dx}}x^{2}=2\times x$ 和 ${\frac {d}{dx}}x^{3}=3\times x^{2}$ 有驚人的相似之處嗎？

解開這個謎團的關鍵是資料結構的單孔上下文的概念。想象一個數據結構，它以型別 $X$ 為引數，就像樹的型別 ${\mathit {Tree}}\,X$。如果我們要從結構中刪除一個型別 $X$ 的項，並以某種方式標記現在空的位置，我們就會得到一個帶標記孔的結構。結果被稱為“單孔上下文”，將型別 $X$ 的項插入孔中，就會得到一個完全填充的 ${\mathit {Tree}}\,X$。這個孔充當一個特殊的位置，一個焦點。這些圖說明了這一點。

從 ${\mathit {Tree}}\,X$ 中刪除一個型別為 $X$ 的值會在該位置留下一個空洞。

將 $X$ 插入到一個單洞上下文中，這是一個更抽象的圖示。

當然，我們感興趣的是給出單洞上下文型別的型別，也就是如何在 Haskell 中表示它。問題是如何有效地標記焦點。但正如我們即將看到，透過對我們想要獲取單洞上下文的型別的結構進行歸納來尋找單洞上下文的表示方法，會自動導致高效的資料型別。因此，給定一個數據結構 $F\,X$，它有一個函子 $F$ 和一個引數型別 $X$，我們想要根據 $F$ 的結構計算單洞上下文的型別 $\partial F\,X$。正如我們選擇的符號 $\partial F$ 已經揭示的那樣，構造和、積和複合的單洞上下文的規則與萊布尼茲微分規則完全相同。

單洞上下文		圖示
$(\partial {\mathit {Const_{A}}})\,X$	$=\,0$	在 $A={\mathit {Const_{A}}}\,X$ 中沒有 $X$，因此它的單洞上下文的型別必須為空。
$(\partial {\mathit {Id}})\,X$	$=\,1$	在 $X={\mathit {Id}}\,X$ 中，$X$ 只有一個位置。刪除一個 $X$ 不會在結果中留下任何 $X$。由於只有一個位置可以刪除它，因此 ${\mathit {Id}}\,X$ 只有一個單洞上下文。因此，單洞上下文的型別是單例型別。
$\partial (F+G)$	$=\partial F+\partial G$	作為 $F+G$ 型別的一個元素，它要麼是 $F$ 型別，要麼是 $G$ 型別，一個單孔上下文也要麼是 $\partial F$ 要麼是 $\partial G$.
$\partial (F\times G)$	$=F\times \partial G+\partial F\times G$	一對中的單孔上下文的孔要麼在第一個分量中，要麼在第二個分量中。
$\partial (F\circ G)$	$=(\partial F\circ G)\times \partial G$	鏈式法則。組合中的孔是透過在封閉結構中建立一個孔，並將封閉結構填進去而產生的。

當然，填充孔的函式 plug 的型別是 $(\partial F\,X)\times X\to F\,X$.

到目前為止，語法 $\partial$ 表示函子的微分，即一種具有一個引數的型別函式。但還有一種方便的表示式導向符號 $\partial _{X}$ 更適合計算。下標表示我們要對其進行微分的變數。一般來說，我們有

$(\partial F)\,X=\partial _{X}(F\,X)$

一個例子是

$\partial ({\mathit {Id}}\times {\mathit {Id}})\,X=\partial _{X}(X\times X)=1\times X+X\times 1\cong 2\times X$

當然，$\partial _{X}$ 只是逐點式的，而 $\partial$ 是無點式。

練習
將一些規則改寫成逐點式。例如，乘積法則的左邊變成 $\partial _{X}(F\,X\times G\,X)=\dots$. 為了熟悉單孔上下文，對乘積 $X^{n}:=X\times X\times \dots \times X$ （正好有 $n$ 個因子）進行形式上的求導，並 убедите себя，結果確實對應於相應的單孔上下文。 當然，如果我們不能將型別 $X$ 的值代入單孔上下文，那麼它們將毫無用處。寫出對應於五個規則的 plug 函式。 為兩個變數制定鏈式法則，並證明它會產生單孔上下文。你可以將雙函子 $F\,X\,Y$ 看作是配對 $(X,Y)$ 中的普通函子。當然，你可能需要一個方便的符號來表示雙函子的無點式偏導數。

透過求導實現拉鍊

上面的規則使我們能夠為遞迴資料型別 $\mu F:=\mu X.\,F\,X$（其中 $F$ 是一個多項式函子）構建拉鍊。拉鍊是對大型樹中特定子樹（即型別為 $\mu F$ 的子結構）的關注點。就像上一章一樣，它可以用我們想要關注的子樹和執行緒來表示，也就是子樹所在的上下文。

${\mathit {Zipper}}_{F}=\mu F\times {\mathit {Context}}_{F}$.

現在，上下文是一系列步驟，每一步都會選擇 $F\,\mu F$ 中的特定子樹 $\mu F$。因此，未選擇的子樹由單孔上下文 $\partial F\,(\mu F)$ 收集在一起。這個上下文的孔來自移除我們選擇進入的子樹。將這些內容放在一起，我們得到

${\mathit {Context}}_{F}={\mathit {List}}\,(\partial F\,(\mu F))$.

或者等效地

${\mathit {Context}}_{F}=1+\partial F\,(\mu F)\times {\mathit {Context}}_{F}$.

為了說明具體的計算過程，讓我們系統地構建迷宮資料型別的拉鍊。

data Node a = DeadEnd a
            | Passage a (Node a)
            | Fork a (Node a) (Node a)

這種遞迴型別是不動點

${\mathit {Node}}\,A=\mu X.\,{\mathit {NodeF}}_{A}\,X$

函子的

${\mathit {NodeF}}_{A}\,X=A+A\times X+A\times X\times X$.

換句話說，我們有

${\mathit {Node}}\,A\cong {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A)\cong A+A\times {\mathit {Node}}\,A+A\times {\mathit {Node}}\,A\times {\mathit {Node}}\,A$.

導數為

$\partial _{X}({\mathit {NodeF}}_{A}\,X)\cong A+2\times A\times X$

我們得到

$\partial {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A)\cong A+2\times A\times {\mathit {Node}}\,A$.

因此，上下文為

${\mathit {Context}}_{\mathit {NodeF}}\cong {\mathit {List}}\,(\partial {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A))\cong {\mathit {List}}\,(A+2\times A\times ({\mathit {Node}}\,A))$.

與

data Branch a  = KeepStraightOn a
               | TurnLeft  a (Node a)
               | TurnRight a (Node a)
type Thread a  = [Branch a]

比較，我們看到兩者完全相同，正如預期的那樣！

練習
使用微分，為三叉樹重新構建拉鍊。 構建一個列表的拉鍊。 關於之前練習的修辭問題：列表和棧有什麼區別？

不動點的微分

資料型別不僅僅只有和與積，我們還有固定點運算子，它在微積分中沒有直接對應關係。因此，表格中缺少一個微分規則，即如何對固定點進行微分 $\mu F\,X=\mu Y.\,F\,X\,Y$

$\partial _{X}(\mu F\,X)={?}$.

由於其公式涉及到兩個變數的鏈式法則，我們將它留給練習。相反，我們將針對我們具體的示例型別 ${\mathit {Node}}\,A$ 進行計算。

${\begin{matrix}\partial _{A}({\mathit {Node}}\,A)&=&\partial _{A}(A+A\times {\mathit {Node}}\,A+A\times {\mathit {Node}}\,A\times {\mathit {Node}}\,A)\\&\cong &1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A\\&&+\partial _{A}({\mathit {Node}}\,A)\times (A+2\times A\times {\mathit {Node}}\,A).\end{matrix}}$

當然，進一步展開 $\partial _{A}({\mathit {Node}}\,A)$ 是無用的，但我們可以將其視為一個固定點方程，從而得到

$\partial _{A}({\mathit {Node}}\,A)=\mu X.\,T\,A+S\,A\times X$

其中縮寫為

$T\,A=1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A$

以及

$S\,A=A+2\times A\times {\mathit {Node}}\,A$.

遞迴型別類似於元素型別為 $S\,A$ 的列表，只是空列表被型別為 $T\,A$ 的基本情況取代了。但鑑於列表是有限的，我們可以將基本情況替換為 $1$，並將 $T\,A$ 從列表中拉出來。

$\partial _{A}({\mathit {Node}}\,A)\cong T\,A\times (\mu X.\,1+S\,A\times X)=T\,A\times {\mathit {List}}\,(S\,A)$.

與我們在上一段推匯出的拉鍊進行比較，我們發現列表型別是我們的上下文

${\mathit {List}}\,(S\,A)\cong {\mathit {Context}}_{\mathit {NodeF}}$

以及

$A\times T\,A\cong {\mathit {Node}}\,A$.

最後，我們有

${\mathit {Zipper}}_{\mathit {NodeF}}\cong \partial _{A}({\mathit {Node}}\,A)\times A$.

因此，對我們的具體示例 ${\mathit {Node}}\,A$ 相對於 $A$ 進行微分，會得到一個直到 $A$ 的拉鍊！

練習
使用二元鏈式法則，為不動點的微分建立一個規則。 也許您知道存在歸納的不動點 ($\mu$) 和共歸的不動點 ($\nu$)。共歸的不動點的規則是什麼？

關於引數函式的微分

在查詢單孔上下文的型別時，我們進行 d f(x)/d x。完全可以求解 d f(x)/d g(x) 之類的表示式。例如，求解 d x^4 / d x^2 得到 2x^2，即一個 4 元組的二孔上下文。推導過程如下：設 u=x^2 d x^4 / d x^2 = d u^2 /d u = 2u = 2 x^2。

拉鍊與上下文

然而，一般而言，拉鍊和單孔上下文表示不同的東西。拉鍊關注任意子樹，而單孔上下文只能關注型別建構函式的引數。例如，資料型別

 data Tree a = Leaf a | Bin (Tree a) (Tree a)

是

${\mathit {Tree}}\,A=\mu X.\,A+X\times X$.

拉鍊可以關注頂端為 Bin 或 Leaf 的子樹，但 ${\mathit {Tree}}\,A$ 的單孔上下文的孔，只能關注 Leaf，因為這是 $A$ 型別項所在的地方。 ${\mathit {Node}}\,A$ 的導數之所以恰好是拉鍊，是因為每個子樹的頂端總是用 $A$ 進行修飾。

練習
令人驚訝的是，$\partial _{A}({\mathit {Tree}}\,A)\times A$ 和 ${\mathit {Tree}}\,A$ 的拉鍊，再次證明是相同的型別。進行計算並不困難，但您能解釋一下為什麼會出現這種情況嗎？ 證明$\mu F$ 的拉鍊構造可以透過引入輔助變數$Y$，對$\mu X.\,Y\times F\,X$ 求導，然後重新代入$Y=1$。為什麼這樣有效？ 找到一個型別$G\,A$，其拉鍊不同於單孔上下文。

結論

我們以一個問題來結束本節：微積分中的規則是如何出現在離散環境中的？目前，沒有人知道。但至少，存在一個離散的“線性”概念，即“恰好一次”。將型別$X$ 的項插入單孔上下文的孔中的函式的關鍵特徵是該項恰好使用一次，即線性。我們可以將插入對映視為具有型別

$\partial _{X}F\,X\to (X\multimap F\,X)$

其中$A\multimap B$ 表示線性函式，即不會複製或忽略其引數的函式，如線性邏輯中所述。從某種意義上說，單孔上下文是函式空間$X\multimap F\,X$ 的表示，可以認為是對$X\to F\,X$ 的線性逼近。

另請參閱

• 拉鍊 在 haskell.org wiki 上
• 通用拉鍊及其應用
• 基於拉鍊的檔案伺服器/作業系統
• Scrap Your Zippers: A Generic Zipper for Heterogeneous Types