高中三角函式/實數的圓函式

在本課中，您將以連續的圓函式形式檢視圍繞座標網格旋轉的角度的三角比。將建立旋轉角度增加或減少時比率如何變化以及函式的圖形如何描述這種變化之間的聯絡。

學習目標

將六個基本三角比識別為圍繞原點旋轉角度的連續函式。
識別六個基本三角函式的定義域和值域。
識別弧度和角度度量，以及單位圓上象限角的座標，以及參考角為 30°、45° 和 60° 的座標。

y = sin(x), 正弦圖

到目前為止，您已經對圍繞座標網格的某些旋轉角度的正弦、餘弦和正切的特定值非常熟悉。在數學中，我們經常可以透過觀察一個量在另一個量一致變化時如何變化來了解很多。在這種情況下，當我們逐漸繞座標網格旋轉時，例如，角度的正弦值會發生什麼變化。我們將正弦值視為圍繞座標網格旋轉角度的函式。我們將任何此類函式稱為圓函式，因為它們可以使用單位圓來定義。首先，您可能還記得從前面的部分中，座標網格中標準位置角的正弦是 ${\tfrac {y}{r}}$ 的比率，其中 y 是角度上任何點的 y 座標，r 是從原點到該點的距離。

由於無論半徑 r 的長度如何，給定角度的比率都是相同的，因此我們可以使用單位圓來使事情更方便。

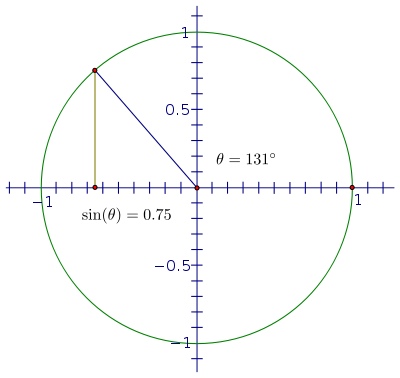
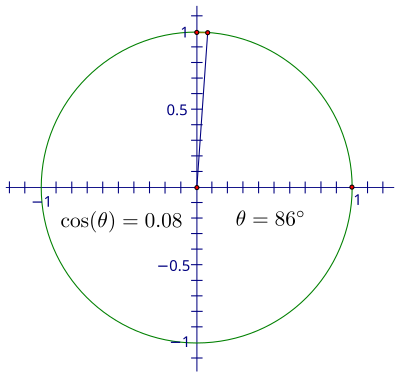
現在分母為 1，所以我們有更簡單的表示式 sin(θ) = y。這樣做的好處是我們可以使用單位圓上點的 y 座標來追蹤 sin(θ) 的值在整個旋轉過程中。想象一下，如果我們從 0 開始，然後逆時針旋轉，角度逐漸增大。由於 y 座標是正弦值，因此請在旋轉時觀察點的垂直高度。

在第一象限，該高度會變大，從 0 開始，一開始增長很快，然後逐漸變慢，直到角度達到 90°，此時，高度達到最大值 1。

當您旋轉到第三象限時，高度的變化現在反轉，並開始向 0 減少。

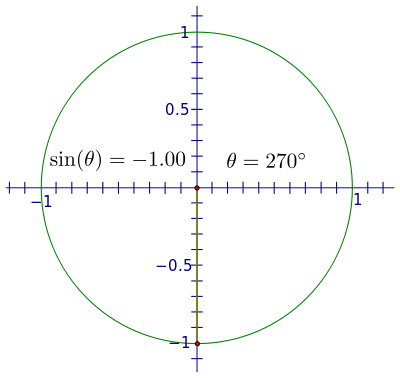
當您開始旋轉到第三和第四象限時，線段的長度會增加，但這次是負方向，在 270° 增長到 −1，並在 360° 回到 0。

完成一次旋轉後，即使角度繼續增加，正弦值也會簡單地重複。如果我們選擇順時針旋轉來研究負角度，也會發生同樣的情況，這解釋了為什麼正弦函式是週期性的。週期是 2π 弧度或 360°，因為這是角度度量所需的度數，在此之前角度的正弦將簡單地重複之前的數值序列。

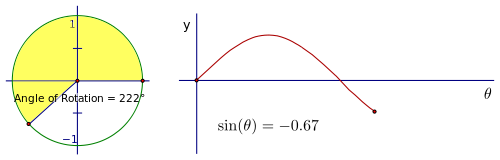
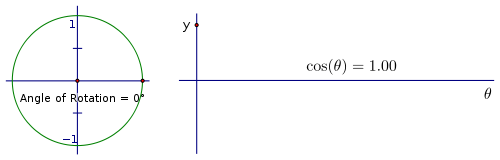
讓我們將這種圓周運動轉換為正弦值與旋轉角度的圖形。以下圖片序列演示了這種聯絡。隨著旋轉角度的增加，觀察角度上點的 y 座標，它水平地進行追蹤。此時忽略水平軸上的值，因為它們只是相對的。重要的是您在圓周旋轉和點垂直高度的變化之間建立聯絡。

請注意，一旦我們旋轉一圈，該點就會沿著相同的值再次追蹤。您看到的紅色曲線是正弦“波”的一個週期。下面的動畫展示了這種情況在“即時”中的發生。

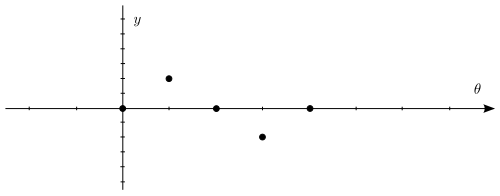
讓我們看一些特定值，以便更精確地繪製正弦函式。由於我們已經知道它們之間的變化情況，因此您可以透過繪製象限角（0、 ${\tfrac {\pi }{2}}$ 、π、 ${\tfrac {3\pi }{2}}$ 、2π）的點來繪製一個相當準確的草圖。

sin(θ) 的值從 0 到 1 到 0 到 −1 然後再回到 0。沿著顯示 θ 的水平軸繪製時，它看起來像這樣

填充它們之間的間隙，並允許多次旋轉以及負角度，從而得出 y = sin(x) 的圖形，其中 x 是任何旋轉角度（通常用弧度表示）

正如我們已經提到的，sin(x) 的週期為 2π。您還應該注意，y 值從不超過 1 或低於 −1，因此正弦波的值域為 {−1 ≤ y ≤ 1}。由於我們可以無限期地繼續繞圓旋轉，因此對角度 x 沒有限制，因此 sin(x) 的定義域是所有實數。

y = cos(x), 餘弦圖

在第 1 章中，您學習了正弦和餘弦密切相關。角度的餘弦與補角的正弦相同。因此，正弦和餘弦波非常相似這一事實應該不會讓您感到驚訝，因為它們都是週期性的，週期為 2π，值域從 −1 到 1，定義域是所有實數角度。

角度的餘弦是 ${\tfrac {x}{r}}$ 的比率，因此在單位圓中，餘弦是旋轉點的 x 座標。如果我們透過旋轉追蹤 x−座標，您會注意到距離的變化類似於 sin(x)，但 cos(x) 從不同的位置開始。0° 角的 x−座標為 1，90° 的 x 座標為 0，因此餘弦值在第一象限從 1 減少到 0。

這是一個類似於我們用於正弦的旋轉序列。這次將旋轉點的 x 座標與它沿著水平線追蹤時的點的高度進行比較。

y = cos(x) 的圖形的週期為 2π。與 sin(x) 一樣，x 值從不“逃離”單位圓，因此它們始終保持在 −1 和 1 之間。餘弦波的值域也是 {−1 ≤ y ≤ 1}。並且也與正弦函式一樣，對旋轉角度沒有限制，因此 cos(x) 的定義域是所有實數。

y = tan(x), 正切圖

正切比作為旋轉角度的函式的圖形呈現了一些複雜性。首先，定義域不再是所有實數角度。您可能還記得，對於某些角度（例如，90° 和 270°），正切是未定義的。正如我們將在本節中看到的，tan(x) 的值域實際上是所有實數。

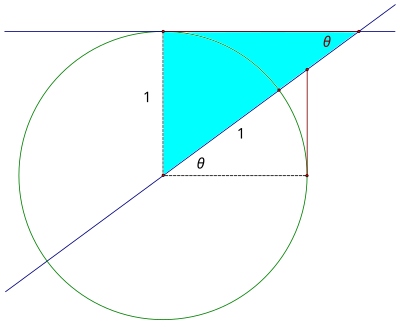
可以使用單位圓上的單一線段來測量六個三角函式中的每一個，但是，其餘函式不像正弦和餘弦那樣明顯。正切函式的名稱來自正切線，正切線是指與圓的半徑垂直於圓上一點的直線，因此該直線僅在一個點上與圓相交。所以，要建立正切線段，我們首先畫一條垂直於x軸的正切線。

如果我們將角度θ穿過單位圓，使其與正切線相交，則正切函式定義為紅色線段的長度。

虛線段為 1，因為它就是單位圓的半徑。回想一下，θ的正切是 ${\tfrac {y}{x}}$ ，因此我們可以使用相似三角形來驗證該線段確實是正切。

\tan(\theta )={\frac {y}{x}}={\frac {t}{1}}=t

\tan(\theta )=t\,\!

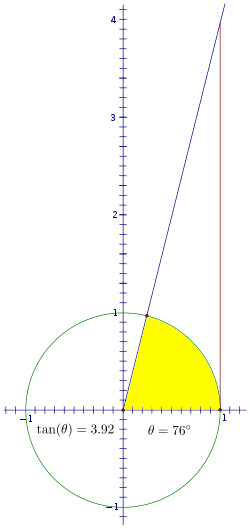
所以，隨著我們增加旋轉角度，思考一下這個線段是如何變化的。當角度為 0 時，線段沒有長度。當我們開始在第一象限旋轉時，它會增加，最初會非常緩慢。

但是，你可以很快看到值超過了 1。隨著角度越來越接近 90°，線段需要向上延伸很遠才能與角度的延伸部分相交，並且它將以越來越快的速度增長。

當我們非常接近y軸時，線段變得無限大，直到角度真正達到 90°，此時角度的延伸部分和正切線將實際平行，因此永遠不會相遇！

這意味著正切線段的長度沒有定義，或者，可以將其理解為，正切線段無限大。

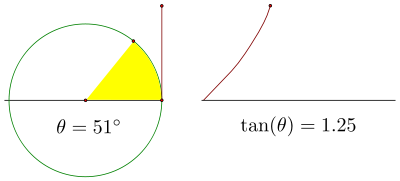
在繼續之前，讓我們看一下該圖形在第一象限的部分。正切從 0 開始，對應 0° 角，然後最初緩慢增加。隨著我們接近 90° 旋轉，該增量變得更加陡峭。

再次，這些圖形中x軸上的一個小間斷將更清楚地表明這兩個需要注意的概念並排位於同一座標系中。

事實上，隨著我們無限接近 90°，正切值無限制地增加，直到我們真正達到 90°，此時正切是未定義的。圖形無限接近但沒有接觸的直線稱為漸近線。因此正切函式在 90° 處有一個漸近線。

當我們旋轉超過 90° 時，現在角度的延伸部分和正切線的交點實際上位於x軸下方。這與我們對第二象限角的正切為負的認識非常吻合。它將首先非常負，但隨著角度旋轉，線段變短，達到 0，然後隨著角度進入第三象限，再次回到正數。

隨著線段接近 270°，它將再次變得無限大。在 270° 處未定義後，角度進入第四象限，並且再次從無限負值變為接近零，直到我們完成完整的旋轉。

所以，這個運動在多個旋轉中繪製的圖形將如下所示

注意，x軸以弧度（不是以π為單位）測量。我們的漸近線每π弧度出現一次，從 ${\tfrac {\pi }{2}}$ 開始。因此，圖形的週期為π弧度。定義域為所有實數，除了 ${\tfrac {\pi }{2}}$ 、 ${\tfrac {3\pi }{2}}$ 、− ${\tfrac {\pi }{2}}$ 等處的“空洞”，值域為所有實數。

三個倒數函式：cot(x)、csc(x) 和 sec(x)

餘切

餘切是正切的倒數，因此在y軸上的一點畫正切線並延長角度（而不是x軸）來生成餘切的圓函式是有意義的。

我們可以再次使用相似三角形來驗證這一點。因為假定的餘切線段平行於黃色三角形的底邊，所以角度θ位於對角，三角形確實是相似的，即使它們的位置顛倒。

所以，

\cot(\theta )={\frac {x}{y}}={\frac {t}{1}}=t

\cot(\theta )=t\,\!

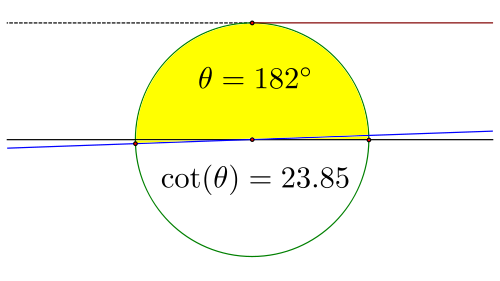
現在我們已經建立了餘切線段，思考一下當我們從 0° 開始繞座標網格旋轉時，這條線段是如何變化的。首先，在 0° 本身，餘切是未定義的，因為線段平行於角度 θ 的射線。當我們開始增加旋轉角度時，線段將變得非常大，並且在我們接近 90° 時開始變小，一開始速度非常快，但隨著它越來越接近 90° 時的 0 長度，速度會變慢。

經過 90° 後，線段將再次開始變長，但這次它將在負方向上，一開始緩慢增加，然後在負方向上無限增大，直到 180°，此時它再次變得未定義。

經過這一點後，週期性行為開始出現，當我們從 180° 旋轉回 360° 時，該函式現在重複相同的值序列。

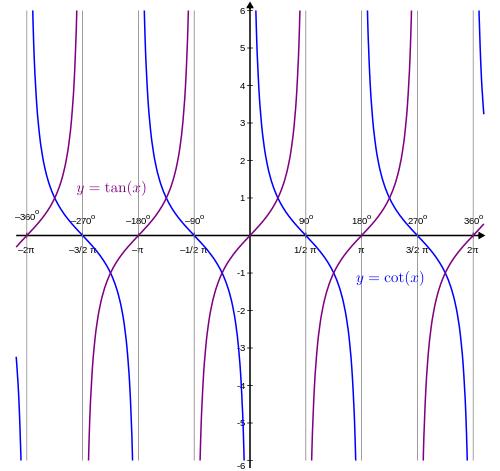
在幾個週期內將此運動軌跡繪製在圖形上，得到

記住餘切和正切互為倒數，因此在正切等於 0 的任何點，餘切都將是未定義的，而在正切未定義的任何點，餘切等於 0。

您可能還會注意到，這些圖形始終在 1 和 -1 處相交。這些是具有 45° 參考角的角度，這些角度的正切和餘切總是等於 1 或 -1。一個函式及其倒數是相同的唯一值是 1 和 -1 是有道理的。當我們檢視餘割和正割與其倒數正弦和餘弦的比較時，請記住這一點。

餘切函式的定義域是所有實數角度，除了 π 的倍數 {… − 2π. − π.0, π, 2π …}。值域是所有實數。

餘割

找到餘割線段有很多可能的方法。一種方法是檢視由余切線段形成的直角三角形，並使用勾股定理來生成餘割。

a^{2}+b^{2}=c^{2}\,\!

1^{2}+\left({\frac {x}{y}}\right)^{2}=c^{2}

\left({\frac {y}{y}}\right)^{2}+\left({\frac {x}{y}}\right)^{2}=c^{2}

{\frac {y^{2}}{y^{2}}}+{\frac {x^{2}}{y^{2}}}=c^{2}

{\frac {y^{2}+x^{2}}{y^{2}}}=c^{2}

從單位圓中的原始三角形，y² + x² = r²

{\frac {r^{2}}{y^{2}}}=c^{2}

\left({\frac {r}{y}}\right)^{2}=c^{2}

由於 ${\tfrac {r}{y}}$ 是餘割，則餘割必須與邊 c 相同。

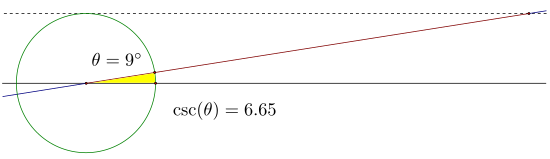
追蹤這條線段的長度，它在 0° 時未定義，對於非常小的角度來說是無限大的，在 90° 時減小到 1，然後無限增大，直到在 180° 時未定義。這個過程從 180° 重複到 360°，但是，線段從無限負開始，在 270° 時增加到 -1，然後接近無限負長度。

因此，該函式的週期為 2π，定義域為所有實數角度，除了 π 的倍數 {… −2π, −π, 0, π, 2π …}。值域是所有大於 1 或小於 -1 的實數。

然後圖形將如下所示

這是 y = sin(x) 的圖形

再次注意 0 處的倒數關係和漸近線。還要注意圖形在 1 和 -1 處的交點。許多學生在看到餘割圖形的一半週期時會想起拋物線。雖然它們在每個都有一個區域性最小值或最大值並且它們在相同的方向開始和結束方面相似，但比較到此為止，它們不應被視為拋物線。定義圖形值，因此也定義圖形形狀的數學完全不同於拋物線的二次函式。

正割

與正弦和餘弦之間的關係非常相似，正割和餘割也有很多相似之處。用於生成 y = sec(x) 的線段如下所示

你將在練習部分演示這一點。這個線段在 0° 時為 1 個單位，然後在第一象限增長，並在 90° 時未定義。它在第二象限無窮地縮小到 −1，然後在第三象限再次向無窮負方向伸長，並在 270° 時未定義。將此運動轉換為 y = sec(x) 的圖形，得到

將它與餘弦圖形進行比較

週期為 2π，範圍與 y = csc(x) 相同 {y : y ≥ 1 或 y ≤ −1}，定義域為所有實數角度，除了 ${\tfrac {\pi }{2}}$ 的倍數 {… − ${\tfrac {3\pi }{2}}$ , − ${\tfrac {\pi }{2}}$ , ${\tfrac {\pi }{2}}$ , ${\tfrac {3\pi }{2}}$ …}.

課程總結

透過將它們視為繞以原點為中心、半徑為一的圓旋轉的點 (x, y) 來考慮，可以將定義為直角三角形中比率的六個三角函式置於座標網格的上下文中。這個圓被稱為**單位圓**。旋轉角的正弦是點的 y 座標，旋轉角的餘弦是 x 座標，切線是 ${\tfrac {y}{x}}$ 。其他三個比率的值；餘切、餘割和正割也可以根據它們的倒數關係找到，但所有這些值都可以通過幾何方式構造為單位圓上旋轉角周圍的各種線段。與其找到孤立的值，不如將每個比率視為旋轉角的**函式**。這些被稱為**圓函式**。以下是六個圓三角函式的定義域和值域。

表 2.3
函式	定義域	值域
sin(x)	所有實數	{y : −1 ≤ y ≤ 1}
cos(x)	所有實數	{y : −1 ≤ y ≤ 1}
tan(x)	{x : x ≠ n · ${\tfrac {\pi }{2}}$ ，其中 n 是任何奇數整數}	所有實數
csc(x)	{x : x ≠ nπ，其中 n 是任何整數}	{y : y > 1 或 y < −1}
sec(x)	{x : x ≠ n · ${\tfrac {\pi }{2}}$ ，其中 n 是任何奇數整數}	{y : y > 1 或 y < −1}
cot(x)	{x : x ≠ n · ${\tfrac {\pi }{2}}$ ，其中 n 是任何奇數整數}	所有實數

複習問題

證明該圖中邊 A 等於 sec(θ)。
在第 1 章中，你學習了 tan²(θ) + 1 = sec²(θ)。使用該圖和問題 1 的結果來證明這個恆等式。
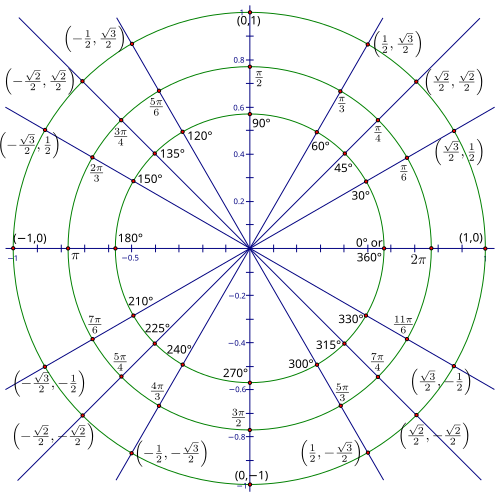
該圖顯示了單位圓，其中所有角度的參考角為 30°、45° 和 60°，以及象限角。標註單位圓上所有點的座標。在最小的圓圈上，以度數標註角度，在中間的圓圈上，以弧度標註角度。
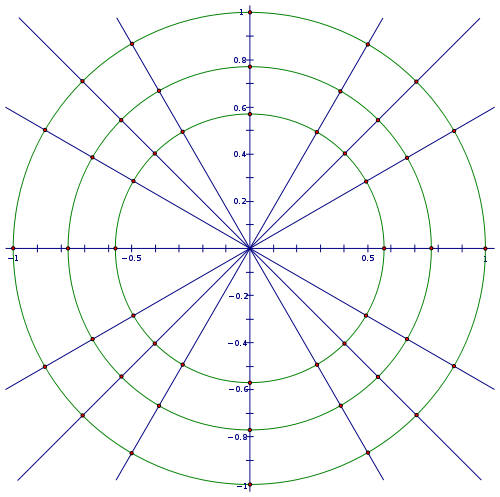
在以下圖中繪製並標註表示六個三角函式（正弦、餘弦、正切、餘割、正割、餘切）的線段。
以下哪些選項顯示了當 x 從 0 增加到 ${\tfrac {\pi }{2}}$ 時都增加的函式？
(a) sin(x) 和 cos(x)

(b) tan(x) 和 csc(x)

(c) sec(x) 和 cot(x)

(d) csc(x) 和 sec(x)
當 x 從 ${\tfrac {3\pi }{2}}$ 增加到 2π 時，以下哪些陳述是正確的？
(a) cos(x) 趨近於 0

(b) tan(x) 變得無窮大

(c) cos(x) < sin(x)

(d) cot(x) 變得無窮小

複習答案

使用相似三角形

所以

${\frac {x}{1}}=$	${\frac {1}{A}}$
$Ax=\,\!$	$1\,\!$
$A=\,\!$	${\frac {1}{x}}$
$\cos(\theta )=\,\!$	$x\,\!$
${\frac {1}{\cos(\theta )}}=$	${\frac {1}{x}}$
${\frac {1}{\cos(\theta )}}=$	$\sec(\theta )={\frac {1}{x}}$
$\therefore \sec(\theta )=\,\!$	$A\,\!$