高中三角函式/弧度制應用

在本課中，您將把弧度制應用於涉及旋轉的各種問題解決情境中。

學習目標

• 使用弧度制解決涉及旋轉角度的問題。
• 透過計算弧長來解決問題。
• 透過計算扇形面積來解決問題。
• 根據中心角和半徑來近似估計弦長。

旋轉

示例 1 時鐘的指標顯示 11:20。用弧度制將時針和分針形成的鈍角表示為最接近的十分之一弧度。 下圖顯示了指標在指定時間的位置。 解決方案: 由於時鐘上有 12 個刻度，每個小時標記之間的角度為 ${\tfrac {2\pi }{12}}$ = ${\tfrac {\pi }{6}}$（或 30°）。因此，12 和 4 之間的角度為 4 · ${\tfrac {\pi }{6}}$ = ${\tfrac {2\pi }{3}}$（或 120°）。由於從 12 到 4 的旋轉是完整旋轉的三分之一，因此假設時針連續移動，並且已經移動了 11 和 12 之間距離的三分之一，這似乎是合理的。因此，${\tfrac {2}{3}}$ · ${\tfrac {\pi }{6}}$ = ${\tfrac {2\pi }{18}}$，因此角度的總量為 ${\tfrac {2\pi }{18}}$ + ${\tfrac {2\pi }{3}}$ = ${\tfrac {2\pi }{18}}$ + ${\tfrac {12\pi }{18}}$ = ${\tfrac {14\pi }{18}}$。使用計算器近似角度將得到 14π/18 2.44346 最接近的十分之一弧度是 2.4 弧度。

弧長

圓上弧的長度取決於旋轉角度和圓的半徑長度。如果你還記得上一課的內容，我們將弧度定義為一個角度為θ的弧的長度，以弧度為單位，定義為一個半徑長度擷取的弧的長度，因此半旋轉為 π 弧度，或略大於圓周的 3 個半徑長度。如果半徑為 4 釐米？半圓弧的長度將為 π 個半徑長度，即 4π 釐米。

這得出了一個可以用來計算任何弧長的公式。

$s=r\theta \,\!$

其中s 是弧長，r 是半徑，θ 是以弧度為單位的角度。

求解此方程以求θ 將得到一個公式，用於在給定弧長和半徑長度的情況下找到弧度量

$\theta ={\frac {s}{r}}$

示例 2 NCAA 籃球場的罰球線寬 12 英尺。在國際比賽中，它只有大約 11.81 英尺。NCAA 球場罰球線上方半圓的長度比國際比賽長多少？ 解決方案: 弧長計算 NCAA 國際 s1 = rθ s2 = rθ s1 = 6(π) s2 ≈ 5.905(π) s1 = 6π s2 ≈ 5.905π 因此答案約為 6π − 5.905π ≈ 0.095π。 .095π .0.29845130209103 這大約是 0.3 英尺，或大約 3.6 英寸。

示例 3 兩個連線的齒輪正在旋轉。較小的齒輪的半徑為 4 英寸，較大的齒輪的半徑為 7 英寸。當較小的齒輪完成一次完整旋轉時，較大的齒輪旋轉的角度是多少？ 解決方案: 由於藍色齒輪完成一次完整旋轉，因此所行進的弧長為 s = rθ s = 4 · 2π 因此，較大切圓上的 8π 弧長將形成以下角度 θ = ${\tfrac {s}{r}}$ θ = ${\tfrac {8\pi }{7}}$ θ ≈ 3.6 所以這個角度大約是3.6弧度。 3.6 · ${\tfrac {180}{\pi }}$ ≈ 206°

扇形面積

最常見的幾何公式之一是圓形的面積

$A=\pi r^{2}\,\!$

就角度旋轉而言，這是由2π弧度產生的面積。

$2\pi {\text{ radian angle}}=\pi r^{2}{\text{ area}}\,\!$

半圓或π弧度旋轉將產生一個圓形的部分，或稱為扇形，其面積等於圓形面積的一半，即

${\frac {1}{2}}\pi r^{2}$

因此，1弧度角將定義一個扇形的面積等於

${\frac {2\pi }{2\pi }}=$	${\frac {\pi r^{2}}{2\pi }}$
$1=\,\!$	${\frac {1}{2}}r^{2}$

由此我們可以確定任何角度θ弧度所產生的扇形面積為

$A={\frac {1}{2}}r^{2}\theta$

示例4 作物通常採用中心支點灌溉技術種植，這種技術會形成圓形田地。 以下是堪薩斯州使用這種灌溉系統的田地的衛星影像。 如果灌溉管長度為450米，那麼旋轉${\tfrac {2\pi }{3}}$弧度後可以灌溉的面積是多少？ 解決方案: 使用公式 $A={\frac {1}{2}}r^{2}\theta$ $A={\frac {1}{2}}(450)^{2}\left({\frac {2\pi }{3}}\right)$ .5*4502*2π/3 212057.5041 該面積約為212,058平方米。

弦長

你可能還記得你在幾何學習中，弦是連線圓周上兩點的線段。

${\overline {AB}}$是圓形中的弦。

如果我們知道角度和半徑的長度，就可以計算出任何弦的長度。因為弦的每個端點都在圓周上，所以從圓心到A和B的距離與半徑長度相同。

接下來，如果我們平分這個角，角平分線必須垂直於弦（我們將在幾何課上證明這一點）。這就形成一個直角三角形。

現在我們可以使用一個簡單的正弦比率來找到弦的一半，這裡稱為c，然後將結果加倍以找到弦的長度。

$\sin \left({\frac {\theta }{2}}\right)=$	${\frac {c}{r}}$
$c=\,\!$	$r\cdot \sin \left({\frac {\theta }{2}}\right)$

所以弦長為

$2c=2r\sin \left({\frac {\theta }{2}}\right)$

例 5 求半徑為 8 釐米，圓心角為 110° 的圓的弦長。將答案四捨五入到最接近的毫米。 解決方案: 先估計答案始終是一個好的問題解決技巧。估計量度的思考過程可能如下所示 角度略大於 90° 或 ${\tfrac {\pi }{2}}$ 弧度。 ${\tfrac {\pi }{2}}$ 弧度略大於 1.5 個半徑長度。一個半徑是 12，所以我們可能期望答案略大於 12 釐米。讓我們看看實際答案與之相比如何。 我們必須首先將角度測量轉換為弧度 $100\cdot {\frac {\pi }{180}}={\frac {11\pi }{18}}$ 使用公式，弦長的一半應等於圓的半徑乘以角度一半的正弦值。 ${\frac {11\pi }{18}}\cdot {\frac {1}{2}}={\frac {11\pi }{36}}$ 8 · sin $\left({\tfrac {11\pi }{36}}\right)$ （確保你的計算器處於弧度模式！） 將結果乘以 2。 8sin(11π/36) 6.553216354 Ans*2 13.10643271 因此，弧長約為 13.1 釐米。根據我們的估計，這似乎非常合理。

複習題

1. 右邊的影像顯示了巴西巴拉那州庫裡提巴的 24 小時制時鐘。

   (a) 時鐘上每個數字之間的角度用以下方式表示

   i. 用 π 表示的精確弧度量？

   ii. 四捨五入到最接近的十分之一弧度？

   iii. 角度量？

   (b) 估計顯示時間時指標之間的角度量

   i. 四捨五入到最接近的整數度

   ii. 用 π 表示的弧度量

2. 

   右邊的圖片是新澤西州普林斯頓普林斯頓大學校園建築的窗戶。

   (a) 用 π 表示的窗戶中央小圓上兩個相鄰圓點的精確弧度量是多少？

   

   (b) 如果這個圓的半徑約為 0.5 米，則每個相鄰點中心之間的弧長是多少？將答案四捨五入到最接近的釐米。

   

3. 現在看看窗戶中下一個更大的圓。

   

   (a) 找到這個窗戶中兩個相鄰點之間的精確弧度量，用 π 表示。

   (b) 這個窗戶玻璃部分的半徑約為 1.20 米。計算突出顯示的弦長估計值，四捨五入到最接近的釐米。解釋你解決方法背後的推理。

   

4. 州冠軍賽將在雷·迪亞茲紀念體育館舉行。座位在球場周圍形成一個完美的圓圈。阿基米德高中的校長收到了以下圖表，顯示了分配給學校學生的座位。
   
   從球場中心到看臺起點距離為 55 英尺，從球場中心到終點距離為 110 英尺。計算以下各組的近似平方英尺數

   (a) 來自阿基米德的學生

   (b) 普通入場

   (c) 新聞界和官員

5. 

   右邊是科羅拉多州旗的圖片。事實證明，金色圓圈的直徑是 ${\tfrac {1}{3}}$ 國旗的總高度（與黃色條紋的寬度相同），紅色圓圈的外徑是 ${\tfrac {2}{3}}$ 國旗的總高度。紅色條帶缺失部分形成的角度為 ${\tfrac {\pi }{4}}$ 弧度。在一面高 33 英寸的旗幟上，紅色部分的面積是多少平方英寸（四捨五入到最接近的平方英寸）？

複習答案

1.  

   (a) i. ${\tfrac {\pi }{12}}$

       ii. ≈ 0.3 弧度

       iii. 15°

   (b) i. 20°。答案可能會有所不同，約為 15° 且小於 25° 都是合理的。

       ii. ${\tfrac {\pi }{9}}$。同樣，答案可能會有所不同。

2.  

   (a) ${\tfrac {\pi }{6}}$

   (b) ≈ 26 釐米

3.  

   (a) ${\tfrac {\pi }{16}}$

   (b) 為了簡化，我們假設弦延伸到每個點的中心。我們需要找到連線這兩個點的圓心角的度數。
   
   由於有 13 個點，該角為 ${\tfrac {13\pi }{16}}$。弦的長度則為

   $=2r\sin \left({\frac {\theta }{2}}\right)$

   $=2\cdot 1.2\cdot \sin \left({\frac {1}{2}}\cdot {\frac {13\pi }{16}}\right)$

   2*1.2sin(13π/32)

   2.296656806

   弦的長度大約為 2.30 釐米。

4. 每一段都是 ${\tfrac {\pi }{6}}$ 弧度。因此，看臺每一部分的面積為外扇形面積減去內扇形面積

   (a) 學生佔有四部分，約為 9,503 平方英尺

   (b) 有三部分為普通入場區，約為 7,127 平方英尺

   (c) 只有一個新聞和官員區，約為 2,376 平方英尺

   $A=A_{\text{outer}}-A_{\text{inner}}\,\!$

   $A={\frac {1}{2}}(r_{\text{outer}})^{2}\cdot {\frac {\pi }{6}}-{\frac {1}{2}}(r_{\text{inner}})^{2}\cdot {\frac {\pi }{6}}$

   $A={\frac {1}{2}}(110)^{2}\cdot {\frac {\pi }{6}}-{\frac {1}{2}}(55)^{2}\cdot {\frac {\pi }{6}}$

   .5*110²*π/6-.5*55²
   *π/6

   2375.829444

   每部分的面積大約為 2376 平方英尺。

5. 解決這個問題有很多不同的方法。以下是一種可能的解決方案。

   首先，計算紅色環的面積，就好像它完全繞著圓圈一樣

   $A=A_{\text{total}}-A_{\text{gold}}\,\!$

   $A=\pi \left({\frac {2}{3}}\cdot 33\right)^{2}-\pi \left({\frac {1}{3}}\cdot 33\right)^{2}$

   $A=\pi \cdot 22^{2}-\pi \cdot 11^{2}\,\!$

   $A=484\pi -121\pi =363\pi \,\!$

   $A\approx 1140.4{\text{ in}}^{2}\,\!$

   

   接下來，計算形成“c”開口的整個扇形的面積。

   $A={\frac {1}{2}}r^{2}\theta$

   $A={\frac {1}{2}}(22)^{2}\left({\frac {\pi }{4}}\right)$

   $A\approx 190.1{\text{ in}}^{2}\,\!$

   

   然後，計算黃色扇形的面積，並從之前的答案中減去它。

   $A={\frac {1}{2}}r^{2}\theta$

   $A={\frac {1}{2}}(11)^{2}\left({\frac {\pi }{4}}\right)$

   $A\approx 47.5{\text{ in}}^{2}\,\!$

   $190.1-47.5=142.6{\text{ in}}^{2}\,\!$

   最後，從第一個計算出的面積中減去這個答案。

   

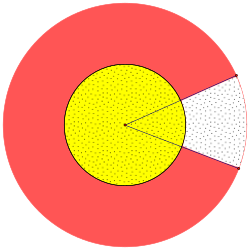
   面積約為 998 平方英寸。

本材料改編自原始的 CK-12 圖書，可在此處找到 此處。本作品根據知識共享署名-相同方式共享 3.0 美國許可協議授權。