高中三角學/弧度制

在本課中，您將被介紹到弧度作為三角學中常用的角度單位。熟練地在度數和弧度之間進行轉換非常重要。最終，就像學習一門外語一樣，當您可以學會用弧度“思考”而不是總是從度數轉換時，您將對弧度制感到舒適。最後，我們將回顧基於 30 度、45 度和 60 度旋轉的基本三角函式的計算。

學習目標

• 定義弧度制。
• 將角度度數轉換為弧度，並將弧度轉換為角度。
• 計算以弧度或角度表示的特殊角的六個三角函式的值。

瞭解弧度制

許多度量單位來自看似隨意和古老的根源。一些甚至隨著時間的推移而改變。例如，米最初旨在基於地球的周長，現在有一個基於特定頻率的相干光的週期數（波長）的極其複雜的科學定義！我們通常使用度數來測量角度，就像我們使用秒來表示分鐘，使用分鐘來表示小時一樣。所有 60 和 12 的倍數，西方文明從大約 60 個世紀前發明的古蘇美爾帝國的六十進位制系統中繼承下來，或多或少——當時時尚的場景是文明的搖籃，大多數部落是遊牧民族，勉強維持生計，不會餓死。

度數到底是什麼？一個度數是圍繞圓形旋轉的完整旋轉的 1/360^th。弧度是三角學中用於測量角度的替代單位，有時被稱為自然角。讓我們看看為什麼可能是這樣。

顧名思義，弧度基於圓形的半徑。事實證明，精確地一弧度是由在單位圓的弧上彎曲單位半徑的長度（弧的長度）所產生的角度。一弧度的旋轉、與該弧度長度相同的半徑和所描繪的一弧度長度的弧——這實際上是“圓形一弧度段的弧長”。反過來：假設一個長度，用該長度做一個圓，稱其為單位（一或底），並在圓周上測量相同的長度。無論長度是多少，該角度始終是一個弧度。
是否有另一個原因它可能被稱為自然角，也許一個與三角學中的 TRI（意思是 THREE）相關的理由，這是我們的研究主題？順便說一句，你可能聽說過常數 PI（'π'），甚至可能知道它大約是 3.1459 個東西。什麼東西？{{efn|關於 PI ('π') 的歷史 你會猜是 3.1459 弧度，並且是正確的嗎？讓我們透過單位分析看看什麼抵消了什麼保留。從上面推斷，我們是否不能寫

段（長度） = 角（弧度）⋅ 半徑長度) ⇔ s = (∅ ⋅ r)，其中 's' 是弧長的常用變數，因此為了使方程與長度作為單位相平衡，弧度必須為 [ 1/(長度/旋轉角) ]——這歸結為旋轉角 因為弧度基於圓形的實際部分而不是任意劃分，所以它是高等數學中更自然的角度單位，當您繼續學習微積分時它將特別有用。

如果我們要繞圓形旋轉一圈怎麼辦？繼續新增半徑長度，我們發現需要超過 6 個半徑長度才能完成旋轉。

但完整旋轉的弧長實際上是周長！周長等於半徑長度的 2π 倍。2π 大約為 6.28，因此周長略大於 6 個半徑長度。或者，用弧度製表示，完整旋轉（360 度）為 2π 弧度。

以此為起點，我們可以輕鬆找到其他角度的弧度制。因此，旋轉的一半，即 180 度，必須為 π 弧度，而 90 度必須為二分之一 π。完成下面的表格

表 2.1

角度（度數）	角度（弧度）
90	${\tfrac {\pi }{2}}$
45
30
60
75

因為 45 是 90 的一半，所以二分之一 π 的一半是四分之一 π。30 是直角的三分之一，所以相乘得到

${\frac {\pi }{2}}\cdot {\frac {1}{3}}={\frac {\pi }{6}}$

並且因為 60 是 30 的兩倍

$2\cdot {\frac {\pi }{6}}={\frac {2\pi }{6}}={\frac {\pi }{3}}$

這是完成的表格

表 2.2

角度（度數）	角度（弧度）
90	${\tfrac {\pi }{2}}$
45	${\tfrac {\pi }{4}}$
30	${\tfrac {\pi }{6}}$
60	${\tfrac {\pi }{3}}$
75	${\tfrac {5\pi }{12}}$

最後一個值是透過新增 30 和 45 的弧度制找到的

${\frac {\pi }{4}}+{\frac {\pi }{6}}=$	${\frac {3\cdot \pi }{3\cdot 4}}+{\frac {2\cdot \pi }{2\cdot 6}}$
${\frac {3\pi }{12}}+{\frac {2\pi }{12}}=$	${\frac {5\pi }{12}}$

可能你已經發現了一個將弧度與角度互換的公式，我們很快就會討論它，但大多數你常用的角度都可以從這張表的值中輕鬆找到，所以根據圓周學習它們可以極大地提高你對弧度的理解。例如，大多數學生髮現記住30和60很容易。30是π的六分之一，60是π的三分之一。如果你知道這些角度，你就可以找到任何以30和60為參考角的特殊角度，因為它們都具有相同的分母。同樣，π的四分之幾的倍數（45度）和π的二分之一的倍數（90度）也是如此。

弧度“計數”

你還記得小時候在芝麻街看伯爵嗎？他會數蘋果之類的物體，“一個蘋果，兩個蘋果，三個蘋果……”然後發出邪惡的笑聲，周圍響起閃電和雷聲。嗯，要成功地使用弧度制，你需要重新學習用弧度而不是蘋果來計數。讓我們開始計數直角，實際上是${\tfrac {\pi }{2}}$弧度。

“一個π的二分之一，兩個π的二分之一（實際上就是π），三個π的二分之一，四個π的二分之一（實際上就是2π）”

圖2.1：用弧度製表示的90度旋轉。

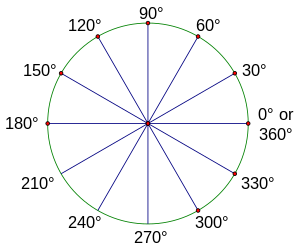
圖2.1：用弧度製表示的90度旋轉。

你剛剛用一次旋轉涵蓋了所有90度的倍數的角度。

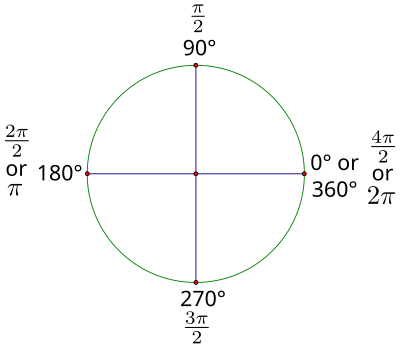
以下是45度角的圖示

圖2.2：45度旋轉。

圖2.2：45度旋轉。

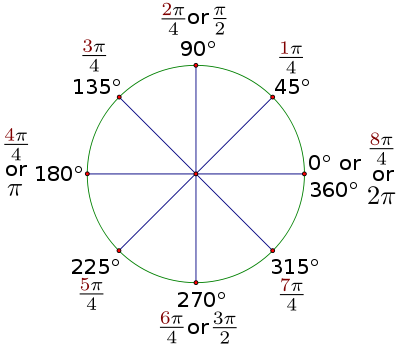
請注意，圖中額外的角度的參考角都是45度，它們的弧度值都是${\tfrac {\pi }{4}}$的倍數。透過計算${\tfrac {\pi }{3}}$和${\tfrac {\pi }{6}}$的倍數，完成以下弧度值。

圖2.3：60度參考角。 圖2.3：60度參考角。

圖2.4：30度參考角。 圖2.4：30度參考角。

圖2.5：60度參考角的弧度製表示，經過一次旋轉。

圖2.5：60度參考角的弧度製表示，經過一次旋轉。

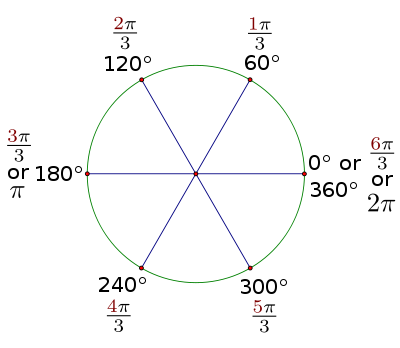圖2.6：30度參考角的弧度製表示，經過一次旋轉。

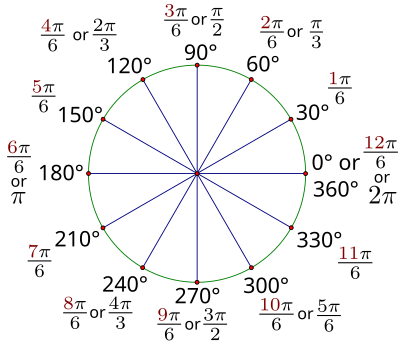圖2.6：30度參考角的弧度製表示，經過一次旋轉。

請注意，所有具有60度參考角的角度都是${\tfrac {\pi }{3}}$的倍數，而所有具有30度參考角的角度都是${\tfrac {\pi }{6}}$的倍數。如果你能學會用這些術語來計數，而不是總是將角度轉換回度，它將幫助你有效地處理大多數你會遇到的弧度值。

對於其他示例，有一個公式。記住，

$\pi {\text{ radians}}=180{\text{ degrees}}\,\!$

如果你將這個等式的兩邊都除以180，你就會發現這個便於轉換的公式

${\frac {\pi }{180}}{\text{ radians}}=1{\text{ degree}}$

所以

${\text{radians}}\cdot {\frac {180}{\pi }}={\text{degrees}}$

如果我們有一個度數，並希望將其轉換為弧度，那麼對上述等式進行運算得到

${\text{degrees}}\cdot {\frac {\pi }{180}}={\text{radians}}$

示例 1 將 ${\tfrac {11\pi }{3}}$ 轉換為度數。 解: 如果按照上一節的內容，你應該認識到這個角度是 ${\tfrac {\pi }{3}}$（或 60 度）的倍數，因此在這個角度中有 11 個獨立的 ${\tfrac {\pi }{3}}$：${\tfrac {\pi }{3}}$ · 11 = 60 · 11 = 660°。 以下是使用公式的結果 ${\text{radians}}\cdot {\frac {180}{\pi }}=$ ${\text{degrees}}\,\!$ ${\frac {11\pi }{3}}\cdot {\frac {180}{\pi }}=$ $11\cdot 60=660^{\circ }\,\!$

示例 2 將 −120° 轉換為弧度制。答案用 π 表示。 解: 使用公式 ${\text{degrees}}\cdot {\frac {\pi }{180}}=$ ${\text{radians}}\,\!$ $-120\cdot {\frac {\pi }{180}}=$ ${\frac {-120\pi }{180}}$ 簡化到最低項得到 $-{\frac {2\pi }{3}}$ 但是，你也可以意識到 120 是 2 · 60。因為 60° 是 ${\tfrac {\pi }{3}}$ 弧度，則 120 是 2 個獨立的 ${\tfrac {\pi }{3}}$，或者 ${\tfrac {2\pi }{3}}$。將其變為負數，你就得到了答案，−${\tfrac {2\pi }{3}}$.

示例 3 將 ${\tfrac {11\pi }{12}}$ 弧度表示為度數。 解: ${\frac {11\pi }{12}}\cdot {\frac {180}{\pi }}=$   $11\cdot 15=\,\!$ $165^{\circ }$

弧度、度數和計算器

大多數科學計算器和圖形計算器都有一個[MODE]設定，可以讓你在弧度和度數之間進行轉換，或者使用任一單位來尋找三角函式的近似值。重要的是，如果你使用計算器來估計三角函式，你應該知道你正在使用的模式。請看以下螢幕

sin(30)

-.9880316241

如果你希望找到 30 度 的正弦，你會根據上一章意識到有些問題，因為它應該是 ${\tfrac {1}{2}}$。事實上，正如你可能已經猜到，計算器將它解釋為 30 弧度。在這種情況下，將模式改為度數並重新計算會給出預期結果。

sin(30)

-.9880316241

sin(30)

.5

科學計算器通常會有一個 3 個字母的顯示，顯示為DEG或RAD來告訴你你正在使用的模式。在計算三角比率之前一定要檢查!

例 4 求 ${\tfrac {3\pi }{4}}$ 的正切。 解: 首先，如果你使用計算器來尋找答案，那你就太丟人了! 你應該知道這個! ${\tfrac {3\pi }{4}}$ 是一個第二象限角，其參考角為 ${\tfrac {\pi }{4}}$（45 度）。${\tfrac {\pi }{4}}$ 的正切是 1，因為正切在第二象限為負，所以答案是 -1。為了在你的計算器上驗證這一點，確保模式設定為 弧度，並計算 ${\tfrac {3\pi }{4}}$ 的正切。 tan(3π/4) -1

例 5 求 cos $\left({\tfrac {11\pi }{6}}\right)$ 的值，保留四位小數。 解: 再次，您應該根據之前的工作知道確切的值。 ${\tfrac {11\pi }{6}}$ 的參考角是 ${\tfrac {\pi }{6}}$（30 度），並且 ${\tfrac {\pi }{6}}$ 的符號是 ${\tfrac {\sqrt {3}}{2}}$。因為 ${\tfrac {11\pi }{6}}$ 在第四象限，因此餘弦為正，因此確切答案為 ${\tfrac {\sqrt {3}}{2}}$。使用計算器得到 cos(11π/6) .8660254038 四捨五入後，結果為 0.8660。您也可以使用計算器驗證它確實是我們確切答案的非常好的近似值。 cos(11π/6) .8660254038 √(3)/2 .8660254038

示例 6 將 1 弧度轉換為度數。 解: 許多學生習慣使用 π 來表示弧度，因此他們錯誤地認為 1 弧度表示 1π 弧度。雖然用 π 表示弧度更方便更常見，但不要忘記，π 弧度實際上是一個數字！它指定了大約 3.14 個半徑長度旋轉所形成的角度。因此，1 弧度是由長度僅為單個半徑的弧所形成的旋轉。回顧圖 1.1。您估計這個角的度數是多少？它顯然是銳角，並且看起來類似於 60° 角。為了找到更接近的近似值，我們將需要公式和計算器。 ${\text{radians}}\cdot {\frac {180}{\pi }}={\text{degrees}}$ 所以 1 弧度將是 ${\tfrac {180}{\pi }}$ 度。使用任何科學計算器或繪圖計算器都可以得到這個度數的合理近似值，大約為 57.3°。 180/π 57.29577951

示例 7 找到具有 sin θ = 0.7071 的銳角θ 的弧度。 解: 首先，重要的是要理解，您的計算器很可能不會以 π 表示弧度，而是以小數近似值表示。在這種情況下，您需要使用反正弦函式。 sin-1(.7071) .7853885734 這個答案可能看起來並不熟悉，但 0.7071 可能聽起來很熟悉。它是 ${\tfrac {\sqrt {2}}{2}}$ 的一個近似值。因此，如您所知，這實際上是一個 45° 角。的確，評估 ${\tfrac {\pi }{4}}$ 將表明計算器正在給出其對弧度測量的最佳近似值。 sin-1(.7071) .7853885734 π/4 .7853981634 如果它們並非完全相同讓您感到困擾，很好，應該這樣！請記住，0.7071 只是 ${\tfrac {\pi }{4}}$ 的一個近似值，因此我們已經從一定的舍入誤差開始。

課程總結

角度可以用度數或弧度來衡量。弧度是由等於彎曲在圓周上的半徑長度的弧長定義的角度。圍繞圓周的一次完整旋轉，或 360° 等於 2π 弧度。要從度數轉換為弧度，請使用以下公式

${\text{degrees}}\cdot {\frac {\pi }{180}}={\text{radians}}$

要從弧度轉換為度數，公式變為

${\text{radians}}\cdot {\frac {180}{\pi }}={\text{degrees}}$

就像學習外語需要記憶詞彙才能取得成功一樣，如果你熟悉象限角的弧度制（90° = ${\tfrac {\pi }{2}}$, 180° = π, 270° = ${\tfrac {3\pi }{2}}$, 360° = 2π) 和特殊角（30° = ${\tfrac {\pi }{6}}$, 45° = ${\tfrac {\pi }{4}}$, 60° = ${\tfrac {\pi }{3}}$），對你理解和使用弧度制將大有幫助。

複習問題

1. 右邊的圖片是出售乳酪的商店的招牌。

   (a) 估計圓中缺失部分的角度大小（度數）。

   (b) 將度數轉換為弧度制。

   (c) 剩餘乳酪部分的弧度是多少？

2. 將以下度數轉換為弧度制，結果用 π 表示，不要使用小數近似值。

   (a) 240°

   (b) 270°

   (c) 315°

   (d) −210°

   (e) 120°

   (f) 15°

   (g) −450°

   (h) 72°

   (i) 720°

   (j) 330°

3. 將以下弧度制轉換為度數

   (a) ${\tfrac {\pi }{2}}$

   (b) ${\tfrac {11\pi }{5}}$

   (c) ${\tfrac {2\pi }{3}}$

   (d) $5\pi \,\!$

   (e) ${\tfrac {7\pi }{2}}$

   (f) ${\tfrac {3\pi }{10}}$

   (g) ${\tfrac {5\pi }{12}}$

   (h) $-{\tfrac {13\pi }{6}}$

   (i) ${\tfrac {8}{\pi }}$

   (j) ${\tfrac {4\pi }{15}}$

4. 圖中顯示了所有象限角以及參考角為 30°、45° 和 60° 的角。在內圓上，用 π 表示所有角的弧度制；在外圓上，用度數表示所有角。
   
5. 使用計算器，找出每個弧度角的度數近似值（精確到小數點後一位）。

   (a) ${\tfrac {6\pi }{7}}$

   (b) 1 弧度

   (c) 3 弧度

   (d) ${\tfrac {20\pi }{11}}$

6. 吉娜想計算 210 的正弦值，並在她的計算器上得到了以下答案

   sin(210)

   .4677185183

   (a) 寫出正確的答案。

   (b) 解釋她錯在哪裡。

7. 完成以下表格。將你的答案寫成最簡根式。

   x	sin(x)	cos(x)	tan(x)
   ${\frac {5\pi }{4}}$
   ${\frac {11\pi }{6}}$
   ${\frac {2\pi }{3}}$
   ${\frac {\pi }{2}}$
   ${\frac {7\pi }{2}}$

答案回顧

1.  

   (a) 答案可能會有所不同，但 120° 似乎比較合理。

   (b) 根據 (a) 部分的答案，合理的答案應該是 ${\tfrac {2\pi }{3}}$

   (c) 同樣，根據 (a) 部分的答案，${\tfrac {4\pi }{3}}$

2.  

   (a) ${\tfrac {4\pi }{3}}$

   (b) ${\tfrac {3\pi }{2}}$

   (c) ${\tfrac {7\pi }{4}}$

   (d) $-{\tfrac {7\pi }{6}}$

   (e) ${\tfrac {2\pi }{3}}$

   (f) ${\tfrac {\pi }{12}}$

   (g) $-{\tfrac {5\pi }{2}}$

   (h) ${\tfrac {2\pi }{5}}$

   (i) $4\pi$

   (j) ${\tfrac {11\pi }{6}}$

3.  

   (a) 90°

   (b) 396°

   (c) 120°

   (d) 540°

   (e) 630°

   (f) 54°

   (g) 75°

   (h) −210°

   (i) 1440°

   (j) 48°

4. 
5.  

   (a) 154.3°

   (b) 57.3°

   (c) 171.9°

   (d) 327.3°

6.  

   (a) 正確答案是 $-{\tfrac {1}{2}}$

   (b) 她的計算器處於錯誤的模式，她計算的是 210 弧度 的正弦值。

7. x	sin(x)	cos(x)	tan(x)
   ${\frac {5\pi }{4}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$1\,\!$
   ${\frac {11\pi }{6}}$	$-{\frac {1}{2}}$	${\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {3}}{3}}$
   ${\frac {2\pi }{3}}$	${\frac {\sqrt {3}}{2}}$	$-{\frac {1}{2}}$	$-{\sqrt {3}}$
   ${\frac {\pi }{2}}$	1	0	未定義
   ${\frac {7\pi }{2}}$	−1	0	未定義

此材料改編自原始的 CK-12 書籍，可在 此處 找到。本作品採用知識共享署名-相同方式共享 3.0 美國許可協議授權。