IB 數學（HL）/進階統計學

主題 8：選修 - 統計學與機率論

正如我們在核心課程的統計學和機率論部分中學到的，期望值 $\mathrm {E} (X)$，或分佈 "X" 的均值 $\mu$ 是

$\mu =\mathrm {E} (X)={\begin{cases}\sum xP(x),&{\mbox{for discrete }}X\\\int xf(x)dx,&{\mbox{for continuous }}X\end{cases}}$

分佈的方差定義為

${\begin{aligned}\sigma ^{2}=\mathrm {Var} (X)&=\mathrm {E} ((X-\mu )^{2})\\&=\mathrm {E} (X^{2})-(\mathrm {E} (X))^{2}\end{aligned}}$

如果 X 是離散的，方差可以定義為

${\begin{aligned}\sigma ^{2}=\mathrm {Var} (X)&=\mathrm {E} ((X-\mu )^{2})\\&=\sum (x-\mu )^{2}P(x)\\&=\sum x^{2}P(x)-\sum \mu ^{2}P(x)\\&=\sum x^{2}P(x)-\mu ^{2}&\left\{\sum P(x){\mbox{ is }}1{\mbox{ and }}\mu {\mbox{ is a constant}}\right\}\\\sigma ^{2}=\mathrm {Var} (X)&=\mathrm {E} (X^{2})-(\mathrm {E} (X))^{2}\end{aligned}}$

期望代數

線性變換

如果對一個分佈進行平移和縮放，均值和方差必須發生變化。這些值根據以下公式變化

$\mathrm {E} (aX+b)=a\mathrm {E} (X)+b$
$\mathrm {Var} (aX+b)=a^{2}\mathrm {Var} (X)$

注意，方差不受 *b* 的值影響，因為分佈的方差永遠不會因分佈的平移而改變。只有代表分佈水平拉伸的值 *a* 會修改分佈的範圍。

獨立隨機變數的線性組合

當一個人對隨機變數 *X* 進行多次取樣時，這些取樣通常是獨立的隨機變數。在這種情況下，必須以不同的方式處理分佈。

$\mathrm {E} (a_{1}X_{1}\pm a_{2}X_{2})=a_{1}\mathrm {E} (X_{1})\pm a_{2}\mathrm {E} (X_{2})$
$\mathrm {Var} (a_{1}X_{1}\pm a_{2}X_{2})=a_{1}^{2}\mathrm {Var} (X_{1})+a_{2}^{2}\mathrm {Var} (X_{2})$

注意，方差總是疊加，而不是減去。此外，隨機變數不一定來自同一個總體 *X*。

這些規則也適用於包含 *n* 個獨立隨機變數的情況。

$\mathrm {E} (a_{1}X_{1}\pm a_{2}X_{2}\pm ...\pm a_{n}X_{n})=a_{1}\mathrm {E} (X_{1})\pm a_{2}\mathrm {E} (X_{2})\pm ...\pm a_{n}\mathrm {E} (X_{n})$
$\mathrm {Var} (a_{1}X_{1}\pm a_{2}X_{2}\pm ...\pm a_{n}X_{n})=a_{1}^{2}\mathrm {Var} (X_{1})+a_{2}^{2}\mathrm {Var} (X_{2})+...+a_{n}^{2}\mathrm {Var} (X_{n})$

該規則的推導超出了本課程大綱的範圍。

平均值和方差的無偏估計量

${\begin{aligned}\mathrm {E} ({\overline {X}})&=\mathrm {E} ({\tfrac {X_{1}+X_{2}+...+X_{n}}{n}})&\\&={\tfrac {\mathrm {E} (X_{1}+X_{2}+...+X_{n})}{n}}&\{{\mbox{Assuming independence}}\}\\&={\tfrac {\mathrm {E} (nX)}{n}}&\{n{\mbox{ of them }}\}\\&={\tfrac {n\mu }{n}}\\\mathrm {E} ({\overline {X}})&=\mu &\therefore {\overline {x}}{\mbox{ or }}\mathrm {E} ({\overline {X}}){\mbox{ is the unbiased estimate of }}\mu \end{aligned}}$

方差的無偏估計量透過將原始方差乘以n/(n-1)來計算

機率分佈函式

離散分佈

二項式，B(n,p)
當X~B(n,p)時，P(X=x)表示在進行n次試驗時獲得x次成功的機率，每次試驗的成功機率為p。
適用於

• 只有兩種可能的結果
• 試驗次數固定
• 每次試驗與其他試驗的結果無關
• 每次試驗的機率保持不變。

負二項式，NB(r,p)
對達到r次成功所需的伯努利試驗B(1,p)次數進行建模。機率質量函式中的組合係數僅僅是為了說明獲得如此多次成功的排列方式數量。

幾何分佈，Geo(p)
對獲得第一次成功所需的伯努利試驗B(1,p)次數進行建模，即類似於NB(1,p)。不需要組合係數，因為一旦獲得第一次成功，"計數"就會停止。因此，結果只有一個可能的排列。

泊松分佈，P_o(m)
泊松分佈測量以下情況下的成功次數：

• 固定時間間隔
• 無限次試驗。

例如，每小時可能會有大量的電話呼入，但如果平均每小時兩次，則這種可能性很小。注意：這假設m是恆定的，但在實際情況下並非如此（例如，電話呼入的頻率取決於一天中的時間、一週中的哪天等）。此類問題通常涉及時間間隔之間的轉換，例如，如果平均每小時兩次呼入，並且需要知道 5 小時內特定次數呼入的機率，則使用的平均值為 10。此外，該分佈的特定之處在於 E(x) = Var(x)。

連續分佈

這些可以遵循任何函式，其中

• ${f(x)}\geq {0}$ 對於所有 ${x}\in$ f(x) 的範圍。
• $\int _{b}^{a}f(x)\,dx=1$ 如果 $f(x)$ 的定義域是 $a\leq x\leq b$。

此外，x 可以是任何值 $-\infty \leq x\leq \infty$，它也在 $f(x)$ 的定義域內。累積頻率是透過積分 $f(x)$ 計算的。
此外，大綱要求瞭解三種特定的連續機率分佈。

指數分佈，Exp(λ)
此分佈對泊松分佈中事件（假設為瞬時）之間的預期間隔進行建模。例如，對於 P_o(2) 每小時的呼叫，每小時的預期呼叫次數為 2；指數分佈的預期值，${\tfrac {1}{\lambda }}$，是半小時。
指數分佈也可以看作是幾何分佈的連續等價物，它對第一次成功之前的時間進行建模。

正態分佈，N(μ,σ²)
這是最有趣的分佈，也是與統計選項最相關的分佈。由於中心極限定理，統計選項的大部分內容都基於正態分佈。在關於正態分佈的問題中，問題必須說明手頭的資料“遵循正態分佈”、“是正態分佈的”等。這使得它易於識別。
標準正態變數Z 遵循該分佈，是一種轉換為Z 分數的方法，這對於計算置信區間和假設檢驗很重要。

正態分佈對二項分佈的近似
對於n 的較大值，X~B(n,p) 可以近似為 X~N(np,npq)。（這可以在直方圖上顯示。）
對於n 應該有多大有不同的估計；大於 5 通常是一個很好的近似，但 IB 說明 $(np)\geq 10$ 和 $(nq)\geq 10$ 作為規則。在不滿足這些條件的情況下，應明確說明近似值不好。

分佈彙總

每個分佈的方程式、函式和符號彙總如下所示。

離散分佈

分佈	符號	機率質量函式	平均值	方差
二項分佈	X~B(n,p)	${\binom {n}{x}}p^{x}(1-p)^{n-x}$ 對於 $x=0,1$	$np$	$np(1-p)$
泊松分佈	X~Pois(m)	${\cfrac {m^{x}e^{-m}}{x!}}$ for $x=0,1,\ldots$	$m$	$m$
幾何分佈	X~Geo(p)	$pq^{x-1}$ for $x=1,2,\ldots$	${\cfrac {1}{p}}$	${\tfrac {q}{p^{2}}}$
負二項分佈	X~NB(r,p)	${\binom {x-1}{r-1}}p^{r}q^{x-r}$ for $x=r,r+1,\ldots$	${\tfrac {r}{p}}$	${\tfrac {rq}{p^{2}}}$

連續分佈

分佈	符號	機率密度函式	平均值	方差
指數分佈	X~Exp($\lambda$)	$\lambda \mathrm {e} ^{-\lambda x},x\geqslant 0$	${\tfrac {1}{\lambda }}$	${\frac {1}{\lambda ^{2}}}$
正態	X~N($\mu ,\sigma ^{2},N$)	${\frac {1}{\sigma {\sqrt {2\pi }}}}\mathrm {e} ^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$	$\mu$	$\sigma ^{2}$

正態分佈

線性組合

通常，組合變數很有用，例如確定$X>Y$的機率。這是透過求解不等式並基於一個新變數來實現的，例如$U$在隨機變數大小上。
$\mathrm {P} (X>Y)\!$
$=\mathrm {P} (X-Y>0).\!$
${\text{let }}U=X-Y\!$

現在我們需要找到$U$，使用以下規則：

• $\mathrm {E} (X\pm Y)=\mathrm {E} (X)\pm \mathrm {E} (Y)$
• $\mathrm {Var} (X\pm Y)=\mathrm {Var} (X)+\mathrm {Var} (Y)$

請注意，方差始終相加。在嘗試組合變數之前，將標準差轉換為方差也很重要。

問題還討論了進行多次選擇的組合。請注意以下區別：

• $U=X_{1}+X_{2}+X_{3}+X_{4}\!$ 和
• $U=4X\!$.

在第一個中，進行了四次獨立選擇。方差變為$4\mathrm {Var} (X)$.
其次，一次抽取的價值乘以四。在這種情況下，方差為 $\mathrm {Var} (4X)=16\mathrm {Var} (X)$。
簡而言之，儘管具有相同的 μ 和 σ，但應將不同的抽取視為獨立的變數。

中心極限定理

從非正態總體 $X$ 中抽取樣本，其平均值為μ 方差為σ²，這些樣本的平均值將正態分佈為 ${\bar {X}}\sim N(\mu ,{\tfrac {\sigma ^{2}}{n}})$，其中n 是每個樣本所基於的資料點數量（樣本量）。當 $n\geq 30$ 時，這適用。

這些樣本必須是獨立的。雖然不需要證明中心極限定理，但瞭解它源於二項分佈可能會有所幫助：要麼 ${\bar {x}}<\mu$ 要麼 ${\bar {x}}\geq \mu$。機率是恆定且獨立的，這意味著樣本均值由二項式函式描述。我們已經知道透過二項分佈的正態近似，當樣本量足夠大時，分佈將近似正態。

對於樣本量 $n\geq 30$，這是一個可靠的近似值。請注意，方差，${\tfrac {\sigma ^{2}}{n}}$，正態分佈的方差隨著n 的增大而減小，這意味著機率分佈將更窄，即更精確。使用中心極限定理時，正態分佈的“標準差”，${\tfrac {\sigma }{\sqrt {n}}}$，也被稱為抽樣誤差 或標準誤差。

比例的正態性

具有大樣本量的比例也遵循正態分佈。遵循與樣本均值類似的邏輯，樣本的比例可以是成功或失敗。這種機率被認為是固定的，這意味著分佈是二項式分佈。當樣本量足夠大時，因此存在一個正態分佈，其中 $\mu ={\widehat {p}}$，樣本比例
${\widehat {p}}={\frac {X}{n}},~~~{\text{ where }}{\begin{cases}{\widehat {p}}={\text{ sample proportion}}\\X={\text{ number of successes}}\\n={\text{ sample size.}}\end{cases}}$
如果p 是成功者的真實比例，n 是樣本量，那麼X~B(n,p)。因此，我們可以證明

• 期望值 $\mathrm {E} ({\widehat {p}})=\mathrm {E} ({\tfrac {1}{n}}X)={\tfrac {1}{n}}\mathrm {E} (X)={\tfrac {1}{n}}\times np=p$
  
  
• 方差 $\mathrm {Var} ({\widehat {p}})=\mathrm {Var} ({\tfrac {1}{n}}X)={\tfrac {1}{n^{2}}}\mathrm {Var} (X)={\tfrac {npq}{n^{2}}}={\tfrac {pq}{n}}$
  
  

根據中心極限定理，我們可以說對於較大的n值，${\widehat {p}}\sim \mathrm {N} (p,{\tfrac {pq}{n}})$.

置信區間

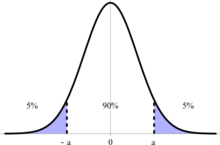90% 置信區間。90% 的資料在 0±a 之內。

置信區間是根據分佈的平均值測量的一個範圍，在這個範圍內，一定比例的樣本位於其中。它通常用百分比表示，例如說“90% 的樣本重量為 2±0.01 公斤”。
置信區間對樣本均值和比例的計算方式相同。在每種情況下，令 $\mu ={\bar {x}}$ 或 $\mu ={\widehat {p}}$。當總體方差未知時，會出現差異。下面將探討這兩種情況。

當 σ 已知時

資料手冊給出了置信區間的表示式：
${\bar {x}}\pm z\times {\frac {\sigma }{\sqrt {n}}}$（當n≥30時）。
這個相同的表示式只是用樣本的標準分佈表示：
${\widehat {p}}\pm z\times {\sqrt {\frac {{\widehat {p}}{\widehat {q}}}{n}}}$（當np≥10或nq≥10時）。

$z$ 是對應置信區間百分比的z分數。可以使用資料手冊最後幾頁的表格或使用計算器上的 invNorm 函式查詢。但是，請注意，輸入 invNorm(.9) 不會給出 90% 置信區間的Z分數。剩下的 10% 必須平均分配到目標範圍的平均值之上和之下，目標範圍在平均值的 90% 之內。因此，z = invNorm(0.95)。這可以在上面的插圖中清楚地看到 - 我們想找到a的值，因此應該使用 0.95 或 0.05。這與雙尾檢驗（下面描述）的概念相同 - 如果我們說 90% 的值低於某個值，那麼我們將使用 invNorm(0.9)。

計算器功能
ZInterval：輸入一組資料或統計資料。請注意，在這兩種情況下，都明確要求 σ。置信水平作為分數。使用資料時，選擇列表名稱並設定頻率=1。
1-PropZInt：x 是n 次試驗中的成功次數。置信水平作為分數。

當 σ 未知時

當總體標準差 σ 未知時，我們必須使用樣本資料來估計它。 $S_{n-1}^{2}$ 用於表示 σ。請注意，樣本標準差 $S_{n}$ 可能在不知道總體標準差的情況下就已知。當 σ 已知時，我們說
${\frac {{\bar {X}}-\mu }{\tfrac {\sigma }{\sqrt {n}}}}=Z$，標準正態分佈 N(0,1)。同樣地，當 σ 未知時的分佈是
${\frac {{\bar {X}}-\mu }{\tfrac {S_{n-1}}{\sqrt {n}}}}=t$，稱為 t 分佈。它只是標準正態曲線 N(0,1) 的一個“更胖”版本。

使用 t 分佈時，請說明自由度：ν = n-1，其中，通常情況下，n 是樣本大小。（這在假設檢驗中具有重要意義。）

計算器函式
TInterval：資料或統計量。使用資料時，與 ZInterval 相同的輸入方法。請注意，$S_{x}$ 等於 $S_{n-1}$，必須使用樣本標準差 $S_{n}$ 透過 $S_{n-1}^{2}={\tfrac {n}{n-1}}S_{n}^{2}$（來自資料手冊）進行手動計算。

確定合適的樣本大小

為了使估計正確，樣本的大小必須足夠大。隨著 n 的增加，方差下降，精度提高（分佈變窄）。
以下示例取自 Haese & Harris 的 IBDP Mathematics (Options)

“如果我們希望 98% 地確信樣本均值與總體均值之間的差值小於 0.3，並且知道總體標準差 σ = 1.365，那麼樣本大小應該多大？”

這意味著 $-0.3<\mu -{\bar {x}}<0.3$ [其中 ${\bar {x}}$ 是與 μ 最遠可接受的點。]

從資料手冊公式
$\mu ={\bar {x}}\pm z\times {\tfrac {\sigma }{\sqrt {n}}}$
我們知道

${\bar {x}}-z\times {\tfrac {\sigma }{\sqrt {n}}}<\mu <{\bar {x}}+z\times {\tfrac {\sigma }{\sqrt {n}}}$

而 invNorm(0.99) [不是 0.98!] 是 2.326
$-2.326{\tfrac {\sigma }{\sqrt {n}}}<\mu -{\bar {x}}<2.326{\tfrac {\sigma }{\sqrt {n}}}$

$\therefore 2.326{\tfrac {\sigma }{\sqrt {n}}}=0.3$

${\sqrt {n}}={\tfrac {2.326\sigma }{0.3}}={\tfrac {2.326\times 1.365}{0.3}}\approx 10.583$

$n\approx 112$
因此，需要抽取 112 個樣本才能 98% 確定樣本均值與總體均值之間的差異小於 0.3（n 向上取整至 112）。

請注意，對於**比例**，${\widehat {p}}$ 可能並不總是已知的。在這種情況下，應該使用最大的可能誤差，即
$\pm z{\sqrt {\tfrac {\left({\frac {1}{2}}\right)\left({\frac {1}{2}}\right)}{n}}}\to \pm z{\tfrac {1}{2{\sqrt {n}}}}$
如上所述，這等於最大可接受範圍，例如 0.03，如果比例必須“在 3% 以內”。

顯著性/假設檢驗

假設檢驗的目的是在特定顯著性水平下考慮假設的有效性，並得出關於其準確性的結論。想法是

• 制定一個假設
• 收集樣本資料
• 確定資料是否支援假設

顯著性水平很像顯著性檢驗的置信水平。例如，90% 的置信區間包含 90% 的分佈，而 10% 的顯著性水平意味著假設為真或假的可能性為 90%（10% 的誤差機率）。

零假設和備擇假設

在任何假設檢驗中，都會有兩個相互排斥的假設

• $H_{0}$，零假設，它陳述的是*相等*。在被證明為假之前，它被認為是正確的。
• $H_{1}$，備擇假設，如果$H_{0}$ 被隨機樣本資料證明為假，就會被採用。

例如，檢驗每小時電話呼叫次數的平均值是否大於 6

• $H_{0}:\mu =6$
• $H_{1}:\mu >6$

備擇假設可以是單邊的，如上所示，也可以是雙邊的。如果我們想證明電話呼叫的平均數量**不等於** 6，我們會說 $H_{0}:\mu \neq 6$. 這意味著要麼 $\mu >6$ **或** $\mu <6$. 這在機率計算方式上略有不同（參見置信區間中的 invNorm() 引數），但很大程度上由計算器處理。

均值和比例的顯著性檢驗

要進行檢驗，必須收集資料，從而獲得 ${\bar {x}}$ 的值。然後，根據總體 σ 是否已知，計算z 或 t 分數（$z*\!$ 或 $t*\!$），使用以下公式：

• $z={\frac {{\bar {x}}-\mu }{\tfrac {\sigma }{\sqrt {n}}}}$ 或
• $t={\frac {{\bar {x}}-\mu }{\tfrac {S_{n-1}}{\sqrt {n}}}}$（記住要說明 $n-1$ 自由度）。

使用比例時

• ${\bar {x}}={\widehat {p}}={\tfrac {x}{n}}$
• $\sigma =\sigma _{\widehat {p}}={\sqrt {\tfrac {pq}{n}}}$

所有 CLT 要求都需要滿足各自的方法：$n\geq 30$ 用於樣本均值和 $np\geq 10$ 或 $nq\geq 10$ 用於比例。

下一步是確定 p值 ，即z或t分數出現的機率。對於z分數，可以使用normalcdf()函式進行計算，但對於t分數，整個過程必須在計算器上完成（下面會解釋）。p值衡量的是${\bar {x}}$ 在平均值為μ，標準差為σ的情況下出現的可能性。如果p值較低，則樣本錯誤（可增加樣本量以驗證此點）或平均值不為μ（拒絕零假設）的可能性很高。p值被認為“過低”的臨界值由顯著性水平決定：在0.05（5%）的顯著性水平下，如果p值低於0.05，則$H_{0}$ 將被拒絕。

對於雙尾檢驗 ($\neq$)，p值是機率$\mathrm {P} (t\geq t*)+\mathrm {P} (t\leq -t*)$，而對於單尾檢驗 ($<$ 或 $>$)，它只是$\mathrm {P} (t\geq t*)$ 或 ${\displaystyle z\!$ 和 $z*\!$ 方面的等價物。

假設檢驗步驟

1. 陳述 $H_{0}$，$H_{1}$ 以及檢驗是單尾還是雙尾。
2. 陳述是z分佈還是t分佈，計算相應的檢驗統計量 $z*\!$ 或 $t*\!$。
3. 陳述決策規則（如果p值...則拒絕$H_{0}$）。計算檢驗統計量的p值。
4. 做出決策：“拒絕$H_{0}$”或“接受$H_{1}$”。
5. 簡要陳述將決策置於背景中。

“簡要”陳述將盡可能多地包含來自的資訊。例如，“基於對200塊餅乾的樣本，在1%的顯著性水平下，沒有足夠的證據來接受超過60%的餅乾含有巧克力的假設”。

還有一種稍微不同的方法來判斷計算的z得分是否可接受。而不是將z得分轉換為機率，然後與p值進行比較，而是根據顯著性水平計算臨界值z得分。然後使用邏輯判斷計算的z得分是否落在拒絕域內。例如，在 5% 的顯著性水平下進行檢驗時，一個“<”單尾檢驗$H_{0}$ 可以被拒絕，如果 $z*\!$ < invNorm(0.05)。對於一個“>”單尾檢驗，如果 > invNorm(0.95) 則拒絕，對於一個雙尾檢驗，如果 $\left\vert z*\right\vert \geq$ invNorm(0.975) 則拒絕。

計算器（TI）
計算器函式非常容易使用。一般來說

• $\mu _{0}:$ 和 $\mu :$ 共同構成備擇假設。例如，如果 $H_{0}:\mu <6$ 那麼 $\mu _{0}=6$ 且 $\mu <\mu _{0}$。同樣適用於 “${\text{prop}}$” 和 $P_{0}$ 在 1-PropZTest 中。
• $x$ 是成功的次數
• $n$ 是試驗次數
• ${\bar {x}}$ 是樣本均值
• $\sigma$ 是總體標準差 (z 檢驗) 和 $S_{x}$ 是 $S_{n-1}$，總體方差的無偏估計。

弄清楚哪些變數是已知的，將有助於在不確定如何開始的情況下找到正確的函式。

I 類和 II 類錯誤

• 錯誤地拒絕 $H_{0}$ 是一個I 類錯誤。發生這種情況的可能性等於執行檢驗的顯著性水平。
• 錯誤地接受 $H_{0}$ 是一個 **第二類錯誤**。 隨著顯著性水平的嚴格程度提高，臨界區域縮小，犯第二類錯誤的可能性會增加。 計算犯第二類錯誤的機率需要一個備擇值，即“真實”均值。第二類錯誤是指在均值實際上為b時，接受均值為a的可能性，這意味著犯第二類錯誤的機率取決於b。 因此，第二類錯誤是指在真實均值為b時，獲得樣本均值 ${\bar {x}}$ 的可能性 - 這可以透過使用 normalpdf 計算得出。

卡方分佈

該分佈可用於透過比較預期值與觀察資料來檢驗資料集是否遵循特定分佈。 它還可以用於假設兩個變數是否相互依賴。

卡方 (χ²) 分佈取決於自由度。 自由度越高，它越接近正態曲線。

請注意，所有 χ² 檢驗都是單尾檢驗。 所以不要把p值除以 2 或任何其他奇怪的操作。

擬合優度

對於 GOF 檢驗，$H_{0}$ 說明資料遵循一個分佈，而 $H_{1}$ 說明資料不遵循該分佈。 例如

• $H_{0}$: 資料來自均勻分佈
• $H_{1}$: 資料不是來自均勻分佈。

自由度ν = 類別數 (n) - 限制數 (k)。 當沒有明顯的限制（大多數情況）時，k = 1，這是因為類別數是有限的。 一旦除一個之外的所有值的找到，最後一個類別就無法波動。 這意味著一般來說，對於 GOF 檢驗，ν = n - 1。

要計算資料集遵循特定分佈的機率，請將觀察值和預期值分別輸入到不同的列表中。 如果任何預期頻率低於 5，則將該組與相鄰組合並。 這樣做是為了避免在計算檢驗統計量時除以較小的數字，這會導致過大的值。 由於在執行此操作時類別數會減少，因此相應地減少自由度。 此外，對於每個統計量 ($m,{\bar {x}},p,\mu ,\sigma ^{2}$) 從 ν 中減去 1，這些統計量用於計算預期資料，但本身又是基於觀察資料得出的。

然後使用這些資料執行 χ²GOF 檢驗。 與假設檢驗一樣，p值顯示獲得大於使用此資料集獲得的 χ² 分數的可能性，因此，如果它小於置信度水平 $H_{0}$ 應該被拒絕，可以得出結論，資料在該特定水平下不遵循該分佈。

列聯表

在檢驗變數的獨立性時，使用雙變數列聯表。 這列出了兩個變數的頻率組合。 例如

將吸菸與高血壓相關的列聯表

	吸菸量
高血壓程度	無	中等	重度	總計
嚴重	10	14	20	44
輕度	20	18	31	69
無	40	22	25	87
總計	70	54	76	200

在將資料輸入計算器時，將省略“總計”列和行。 預期值不必手動計算（這可以透過將行總計乘以列總計，然後除以“總計總計”來完成，例如 70×44/200 = 15.4，預期值表中的第一個單元格）。 相反，執行 χ² 檢驗，預期值將被插入到“預期”矩陣中。
χ² 檢驗中的自由度為(行數-1)(列數-1)。
當存在 2×2 列聯表時，ν = 1。 通常情況下，會使用 Yates 的連續性校正，但是這已經從教學大綱中刪除了。 因此，只需照常進行，ν = 1 即可。

對於獨立性檢驗

• $H_{0}$: 變數相互獨立。
• $H_{1}$: 變數相互依賴。

與往常一樣，p值是觀察到的 χ² 值大於觀察到的 χ² 值的機率。 $H_{0}$ 因此，如果顯著性水平低於p值，則拒絕。