舍入誤差

學習目標

識別溢位和下溢誤差的來源
在十進位制表示和浮點表示之間轉換
理解計算機上浮點表示的 IEEE 754 標準
計算表示的機器ε。

整數溢位（誤差）

整數如何在計算機上表示？

大多數計算機使用二進位制補碼表示。假設我們有 4 位來儲存和操作一個整數，我們可能會遇到以下情況

 0111 (7)
+0001 (1)
-----
 1000 (-8)

括號中的數字是 2 的補碼二進位制整數表示的十進位制值。結果顯然是錯誤的，因為新增正數永遠不會導致負數。錯誤的原因是結果超出了 4 位可以使用 2 的補碼錶示法儲存的值範圍。

以下示例由於相同的原因給出了錯誤的答案。無法儲存前面的 1。

 1000 (-8)
+1111 (-1)
-----
10111 (7)

浮點數下溢（誤差）

在數學中，數字具有無限精度，但數字（數字的表示）具有有限精度。三分之一 (1/3) 無法用十進位制精確表示，否則它將需要無限多個數字，這是不可能的。類似地，0.2 無法用二進位制精確表示，這意味著它的二進位制表示不精確（近似）。

當在計算機上計算/計算數字時，數字的表示被操縱，結果很可能是不精確的。這是計算的一個重要限制。本質上，計算機必須被認為是我們模型的一部分，當我們以計算方式解決問題時。我們必須將計算機考慮在內，因為它是一個二進位制計算機，它近似於十進位制數。

一個浮點下溢或下溢發生在計算結果太小而無法儲存時。下溢可能是由於指數的（負）溢位引起的。

11.1875_{10}

的二進位制表示是什麼？

定點表示

任何實數都可以用二進位制表示為定點數。要將數字從其十進位制（基數 10）表示轉換為其二進位制表示，我們需要分別將整數部分和小數部分轉換為二進位制，因為需要不同的方法。請檢視以下資源，瞭解如何做到這一點 [1]。

使用固定數量的數字和固定的小數點，可表示值的範圍是固定的。給定五個數字如下 $nnn.nn_{10}$ ，我們可以表示從 $0.01_{10}$ 到 $999.99_{10}$ 的正值。使用以下科學計數法 $nnn\times 10^{nn}$ ，我們可以表示從 $0.01_{10}$ 到 $99900_{10}$ 的正值，這遠遠大於定點表示的範圍。

浮點表示

使用固定數量的數字，我們可以使用浮點格式表示更大範圍的值。IEEE 754 格式是計算機中數字浮點表示的國際標準。一個 32 位浮點數（單精度）使用三個部分表示，如圖所示：符號位、（有偏）指數和分數。

IEEE 754 單精度浮點數表示的值可以使用以下公式計算

(-1)^{sign}\times 1.fraction\times 2^{exponent-127}

例如，要以 IEEE 單精度浮點數格式儲存 $0.15625_{10}=0.00101_{2}=1.01_{2}\times 2^{-3}$ ，我們需要儲存一個符號位 $0$ （0 表示正數，1 表示負數），一個小數部分 $.01$ ，以及一個偏移指數 $-3_{10}+127_{10}=124_{10}=1111100_{2}$ 。由於除 0 外的所有數字在二進位制“科學”表示中都有一個前導 1，這個 1 在 IEEE 754 格式中沒有儲存，以節省一個位。我們稍後會說明如何表示值 0。

偏移指數只是巧妙地利用了可用位來表示更多值，並使數字比較更快。我們將以 8 位指數為例。在上圖中，我們有 8 位，可以表示 $2^{8}=256_{10}$ 個不同的值。位模式本身沒有內在含義，因此我們可以用它們來表示任何我們想要的東西。綠色部分顯示了這些位模式在被視為無符號整數的二進位制表示時所表示的值。問題是我們也想要表示負值。一種簡單的解決方案是將最左邊的位視為符號位：0 表示正數，1 表示負數，這會導致兩個零 $+0$ 和 $-0$ 。藍色部分顯示了當我們使用 2 的補碼方案來表示正數和負數時，使用相同的一組位模式會發生什麼。回想一下，2 的補碼方案通常用於簡化硬體設計，以便我們可以使用加法來進行減法：a - b 等同於 a + ( -b 的 2 的補碼)。要獲得正整數的 2 的補碼，就是將所有位反轉並加 1。現在所有減法都可以用一次反轉和兩次加法來完成。2 的補碼錶示的問題是，一個看起來“更大”的模式並不一定表示更大的值。

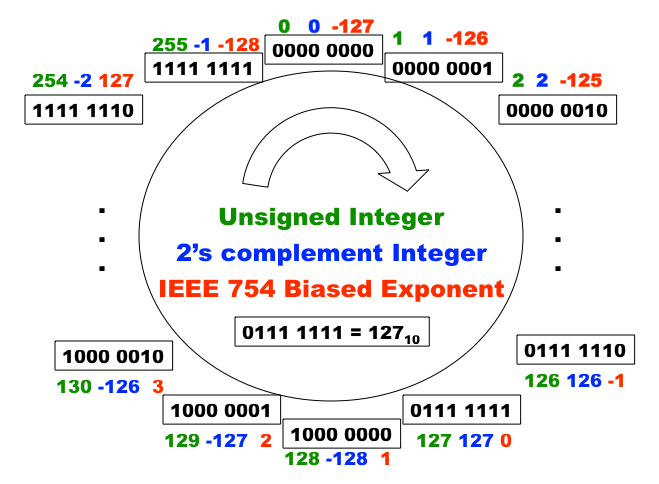
This figure shows how the biased exponent for IEEE 754 works. — 此圖顯示了 IEEE 754 的偏移指數是如何工作的。

紅色部分顯示了由相同一組位模式表示的偏移指數。正如你所看到的，一個看起來“更大”的模式總是表示更大的值，除了全為一的模式，它用於表示一個特殊的值。偏移指數表示的優點是每個值都由一個唯一的模式表示（沒有兩個零），並且比較浮點數更容易。指數放在 IEEE 754 標準中分數的前面，以便可以將浮點數按其位模式作為無符號整數進行比較（速度更快）。

下表顯示了一些由特殊位模式表示的特殊值。

偏移指數	小數部分	數字
00...00	0	0
00...00	非零	非規格化
11...11	0	+/- 無窮大
11...11	非零	NaN（非數字）

因為總是將隱式/隱藏的 1 新增到小數部分以獲得表示的值，所以需要一個特殊的模式來表示零值。現在，除以零的結果可以表示為 +/- 無窮大（整數運算中的除以零會導致程式崩潰）。 ${\sqrt {-4}}$ ，和 $0/0$ 可以表示為 NaN，這有助於除錯你的程式。

這個數字的 IEEE 754 浮點數表示是什麼：

-2.340625\times 10^{1}

這個 IEEE 754 浮點數的十進位制等效值是什麼：1100 0000 1111 0000 0000 0000 0000 0000？

最大的 IEEE 754 單精度浮點數是什麼？

浮點型或科學計數法的缺點是什麼？使用五個數字，我們可以用定點表示法精確地表示 $999.99_{10}$ 。但是，當我們使用以下科學/浮點表示法 $n.nn\times 10^{nn}$ 時，我們可以表示的最接近的值是 $9.99\times 10^{02}$ ，誤差是 $999.99-999=0.99$ - 精度損失。

實數與浮點數數軸

這個圖展示了實數和浮點數數軸的不同。可以做出以下觀察結果

實數軸是連續的、稠密的、無限的。
浮點數（表示）軸是離散的、稀疏的、有限的。
一組實數用同一個浮點數（近似值）表示。
隨著浮點數變大，組的大小也越來越大。

讓我們研究一個具體的例子。使用四個小數位和定點表示法（ $nnn.n$ ），我們可以用相等距離表示 0、0.1、0.2、0.3、...、999.8、999.9。使用浮點表示法（ $+n.nn\times 10^{\pm n}$ ），我們可以表示的最小值為 $1.00\times 10^{-9}=0.\underbrace {0...0} _{8}1$ ，可以表示的最大值為 $1.11\times 10^{+9}=1110000000$ 。現在讓我們看看這種浮點型數字格式在數軸上的某些點周圍可以表示的值

在 0 旁邊： $1.00\times 10^{-9}=0.\underbrace {0...0} _{8}1,1.01\times 10^{-9}=0.\underbrace {0...0} _{8}101,1.02\times 10^{-9}=0.\underbrace {0...0} _{8}102,...$ （連續數字之間的距離為 0.00000000001）
在 1 旁邊： $1.00\times 10^{0}=1,1.01\times 10^{0}=1.01,1.02\times 10^{0}=1.02,...$ （連續數字之間的距離為 0.01）
在 10 旁邊： $1.00\times 10^{1}=10,1.01\times 10^{1}=10.1,1.02\times 10^{1}=10.2,...$ （連續數字之間的距離為 0.1）
在 100 旁邊： $1.00\times 10^{2}=100,1.01\times 10^{2}=101,1.02\times 10^{2}=102,...$ （連續數字之間的距離為 1）
在 1000 附近： $1.00\times 10^{3}=1000,1.01\times 10^{3}=1010,1.02\times 10^{3}=1020,...$ （相鄰數字之間的距離為 10）