線性代數/集合、函式、關係

線性代數
← 證明技巧	集合、函式、關係	許可和歷史 →

集合

數學家使用稱為集合的集合。一個集合可以用大括號之間的列表表示，例如 $\{1,4,9,16\}$ ，或者，如果這很笨拙，可以使用集合生成器符號，例如 $\{x\,{\big |}\,x^{5}-3x^{3}+2=0\}$ （讀作“所有 $x$ 的集合，使得……”）。我們用大寫羅馬字母為集合命名，例如素數 $P=\{2,3,5,7,11,\ldots \,\}$ ，除了少數特殊集合，例如實數 $\mathbb {R}$ 和複數 $\mathbb {C}$ 。為了表示某事物是集合的元素（或成員），我們使用“ ${}\in {}$ ”，因此 $7\in \{3,5,7\}$ ，而 $8\not \in \{3,5,7\}$ .

區分集合與任何其他型別集合的是外延原理，即兩個具有相同元素的集合相等。由於這個原理，在集合中，重複項會合並 $\{7,7\}=\{7\}$ ，順序也不重要 $\{2,\pi \}=\{\pi ,2\}$ .

我們使用“ $\subset$ "表示子集關係： $\{2,\pi \}\subset \{2,\pi ,7\}$ ，而“ $\subseteq$ "表示子集或相等（如果 $A$ 是 $B$ 的子集，但 $A\neq B$ ，那麼 $A$ 是 $B$ 的**真子集**)。這些符號可以反轉，例如 $\{2,\pi ,5\}\supset \{2,5\}$ .

由於外延性，要證明兩個集合相等 $A=B$ ，只需要證明它們具有相同的成員。通常我們會證明互相包含，即 $A\subseteq B$ 和 $A\supseteq B$ 。

集合運算

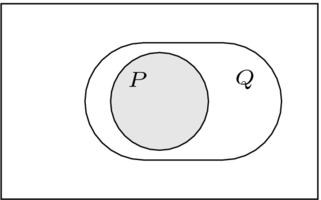
文氏圖在這裡很方便。例如， $x\in P$ 可以表示為

而“ $P\subseteq Q$ "看起來像這樣。

注意，這與“如果……那麼……”命題的圖相同。這是因為“ $P\subseteq Q$ "意味著“如果 $x\in P$ ，那麼 $x\in Q$ ”。

通常，對於每一個命題邏輯運算子，都有一個相關的集合運算子。例如， $P$ 的補集是 $P^{\text{comp}}=\{x\,{\big |}\,{\text{not }}(x\in P)\}$

並集是 $P\cup Q=\{x\,{\big |}\,(x\in P){\text{ or }}(x\in Q)\}$

而交集是 $P\cap Q=\{x\,{\big |}\,(x\in P){\text{ and }}(x\in Q)\}.$

}}當兩個集合沒有公共元素時，它們的交集就是空集 $\{\}$ ，用符號 $\varnothing$ 表示。根據蘊涵定義的“空真”性質，任何集合都包含空集作為子集。

序列

我們還將使用順序重要的集合，且重複元素不合並。這些是序列，用尖括號表示： $\langle 2,3,7\rangle \neq \langle 2,7,3\rangle$ 。長度為 $2$ 的序列有時被稱為有序對，用括號表示： $(\pi ,3)$ 。我們有時也說“有序三元組”、“有序 $4$ 元組”等等。集合 $A$ 中所有有序 $n$ 元組的集合記作 $A^{n}$ 。因此實數對的集合是 $\mathbb {R} ^{2}$ 。

函式

我們首先在初等代數中看到函式，它們被表示為公式（例如， $f(x)=16x^{2}-100$ ），但隨著數學的深入，我們發現了更通用的函式——三角函式、指數函式和對數函式，甚至像絕對值這樣的構造，它們涉及將部分拼湊在一起——我們看到函式不是公式，相反，關鍵在於函式將輸入 $x$ 關聯到一個唯一的輸出 $f(x)$ 。

因此，函式或對映被定義為有序對的集合 $(x,f(x)\,)$ ，使得 $x$ 足以確定 $f(x)$ ，也就是說：如果 $x_{1}=x_{2}$ 那麼 $f(x_{1})=f(x_{2})$ （這個要求被稱為函式是良定義的）。\footnote{更多內容請參見同構部分}

每個輸入 $x$ 是函式的自變數，每個輸出 $f(x)$ 是一個值。所有自變數的集合是 $f$ 的定義域，輸出值的集合是它的值域。通常我們不需要知道值域中有哪些和沒有哪些，而是使用值域的超集，即陪域。函式 $f$ 的記號，定義域為 $X$ ，陪域為 $Y$ 是 $f:X\to Y$ 。

我們有時使用符號 $x{\stackrel {f}{\longmapsto }}16x^{2}-100$ ，讀作“ $x$ 在 $f$ 下對映到 $16x^{2}-100$ ”，或者“ $16x^{2}-100$ 是 $x$ 的“像”。

一些對映，比如 $x\mapsto \sin(1/x)$ ，可以被認為是簡單對映的組合，在這裡， $g(y)=\sin(y)$ 應用於 $f(x)=1/x$ 的像上。 $g:Y\to Z$ 與 $f:X\to Y$ 的 **複合**，是將 $x\in X$ 對映到 $g(\,f(x)\,)\in Z$ 的對映。它記為 $g\circ f:X\to Z$ 。這個定義只有當 $f$ 的值域是 $g$ 的定義域的子集時才有意義。

觀察到恆等對映 ${\mbox{id}}:Y\to Y$ 由 ${\mbox{id}}(y)=y$ 定義，具有以下性質：對於任何 $f:X\to Y$ ，複合函式 ${\mbox{id}}\circ f$ 等於 $f$ 。因此，恆等對映在函式複合中的作用類似於實數加法中的 0，或者類似於乘法中的 1。

根據這個類比，定義對映 $f:X\to Y$ 的左逆為一個函式 $g:{\text{range}}(f)\to X$ ，使得 $g\circ f$ 是 $X$ 上的恆等對映。當然， $f$ 的右逆為一個 $h:Y\to X$ ，使得 $f\circ h$ 是恆等對映。

一個既是 $f$ 左逆又是右逆的對映，簡稱為 **逆對映**。如果存在逆對映，那麼它是唯一的，因為如果 $g_{1}$ 和 $g_{2}$ 都是 $f$ 的逆對映，那麼 $g_{1}(x)=g_{1}\circ (f\circ g_{2})(x)=(g_{1}\circ f)\circ g_{2}(x)=g_{2}(x)$ （中間等式來自函式複合的結合律），因此我們通常稱之為“逆對映”，記為 $f^{-1}$ 。例如，函式 $f:\mathbb {R} \to \mathbb {R}$ 的逆對映，該函式由 $f(x)=2x-3$ 給出，是函式 $f^{-1}:\mathbb {R} \to \mathbb {R}$ ，該函式由 $f^{-1}(x)=(x+3)/2$ 給出。

函式逆對映的 “ $f^{-1}$ " 符號可能令人困惑 - 它並不意味著 $1/f(x)$ 。之所以使用它，是因為它符合一個更大的體系。具有相同陪域和定義域的函式可以迭代，因此對於 $f:X\to X$ ，我們可以考慮 $f$ 與自身的複合： $f\circ f$ 和 $f\circ f\circ f$ 等等。

自然而然地，我們將 $f\circ f$ 寫成 $f^{2}$ ，而 $f\circ f\circ f$ 寫成 $f^{3}$ 等。注意，實數的熟悉指數規則顯然成立： $f^{i}\circ f^{j}=f^{i+j}$ 和 $(f^{i})^{j}=f^{i\cdot j}$ 。與上一段的關係是，當 $f$ 可逆時，將 $f^{-1}$ 表示逆函式，將 $f^{-2}$ 表示 $f^{2}$ 的逆函式等，表明這些熟悉的指數規則在定義 $f^{0}$ 為恆等對映後仍然成立。

如果陪域 $Y$ 等於 $f$ 的值域，那麼我們說該函式是滿射（或映上）。一個函式有右逆當且僅當它是滿射（這並不難驗證）。如果沒有任何兩個引數共享一個像，如果 $x_{1}\neq x_{2}$ 意味著 $f(x_{1})\neq f(x_{2})$ ，那麼該函式是單射（或內射）。一個函式有左逆當且僅當它是單射（這也不難驗證）。

根據上一段，一個對映有逆函式當且僅當它既是滿射又是單射；這樣的函式被稱為雙射。它將定義域中的一個且僅一個元素與值域中的每個元素關聯起來（例如，有限集必須具有相同數量的元素才能以這種方式匹配）。由於單射對映的複合是單射的，滿射對映的複合是滿射的，因此雙射對映的複合是雙射的。

我們有時希望縮小函式的定義域。例如，我們可以取函式 $f:\mathbb {R} \to \mathbb {R}$ ，它由 $f(x)=x^{2}$ 給出，為了使其具有逆函式，我們將輸入引數限制為非負實數 ${\hat {f}}:\mathbb {R} ^{+}\to \mathbb {R}$ 。從技術上講， ${\hat {f}}$ 是一個與 $f$ 不同的函式；我們稱之為 $f$ 在較小定義域上的 **限制**。

關於函式的最後一點： $x$ 或 $f(x)$ 不必是數字。例如，我們可以將 $f(x,y)=x+y$ 視為一個函式，它以有序對 $(x,y)$ 作為引數。

關係

一些熟悉的運算顯然是函式：加法將 $(5,3)$ 對映到 $8$ 。但是，“ $<$ ” 或 “ $=$ ” 呢？我們這裡採用將 “ $3<5$ ” 改寫為 “ $(3,5)$ 屬於關係 $<$ ” 的方法。也就是說，定義集合 $A$ 上的二元關係 為 $A$ 元素的有序對的集合。例如， $<$ 關係是集合 $\{(a,b)\,{\big |}\,a<b\}$ ；該集合中的一些元素是 $(3,5)$ 、 $(3,7)$ 和 $(1,100)$ 。

自然數上的另一個二元關係是等式；該關係正式寫成集合 $\{\ldots ,(-1,-1),(0,0),(1,1),\ldots \}$ 。

另一個例子是“比 $10$ 更接近”，集合 $\{(x,y)\,{\big |}\,|x-y|<10\}$ 。該關係中的一些成員是 $(1,10)$ ， $(10,1)$ 和 $(42,44)$ 。既不是 $(11,1)$ 也不是 $(1,11)$ 是成員。

這些例子說明了定義的普遍性。各種關係（例如，“兩個數字都是偶數”或“第一個數字是第二個數字的數字顛倒”）都包含在定義中。

等價關係

我們需要正式地說明兩個物體在某種程度上是相似的。雖然這些相似的物體並不相同，但它們是相關的（例如，兩個整數“在被 $2$ 除後得到相同的餘數”）。

二元關係 $\{(a,b),\ldots \}$ 當它滿足以下條件時被稱為**等價關係**

自反性：任何物體都與自身相關；
對稱性：如果 $a$ 與 $b$ 相關，那麼 $b$ 與 $a$ 相關；
傳遞性：如果 $a$ 與 $b$ 相關，並且 $b$ 與 $c$ 相關，那麼 $a$ 與 $c$ 相關。

（為了看到這些條件正式化了“相同”，請再次閱讀它們，將“與……相關”替換為“與……相似”。）

一些例子（在整數上）：“ $=$ " 是一個等價關係，" $<$ " 不滿足對稱性，“同號”是一個等價關係，而“比 $10$ 更近”不滿足傳遞性。

劃分

在“同號” $\{(1,3),(-5,-7),(-1,-1),\ldots \}$ 中，有兩類數對，第一類是兩個數都是正數，第二類是兩個數都是負數。所以整數恰好落在兩個類別之一：正數或負數。

集合 $S$ 的劃分是指子集 $\{S_{1},S_{2},\ldots \}$ 的一個集合，使得 $S$ 中的每個元素都屬於且僅屬於一個 $S_{i}$ ： $S_{1}\cup S_{2}\cup \ldots {}=S$ ，並且如果 $i$ 不等於 $j$ ，那麼 $S_{i}\cap S_{j}=\varnothing$ 。想象 $S$ 被分解成不同的部分。

因此，第一段說“同號”將整數劃分為正數和負數。

類似地，等價關係“=”將整數劃分為單元素集。

另一個例子是分數。當然， $2/3$ 和 $4/6$ 是等價分數。也就是說，對於集合 $S=\{n/d\,{\big |}\,n,d\in \mathbb {Z} {\text{ and }}d\neq 0\}$ ，我們定義兩個元素 $n_{1}/d_{1}$ 和 $n_{2}/d_{2}$ 等價，如果 $n_{1}d_{2}=n_{2}d_{1}$ 。我們可以檢查這是否是一個等價關係，也就是說，它是否滿足上述三個條件。有了它， $S$ 被分成若干部分。

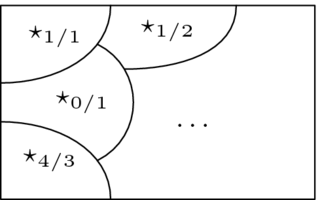
在我們證明等價關係總是導致劃分之前，我們首先說明這個論點。考慮兩個整數之間“奇偶性相同”的關係，集合 $\{(-1,3),(2,4),(0,0),\ldots \}$ （即，“被 $2$ 除後得到相同的餘數”）。我們想說自然數被分成兩個部分，偶數和奇數，在一個部分內部，每個成員的奇偶性與其他成員相同。因此，對於每個 $x$ ，我們定義與它相關的數字集合： $S_{x}=\{y\,{\big |}\,(x,y)\in {\text{same parity}}\}$ 。一些例子是 $S_{1}=\{\ldots ,-3,-1,1,3,\ldots \}$ ，和 $S_{4}=\{\ldots ,-2,0,2,4,\ldots \}$ ，和 $S_{-1}=\{\ldots ,-3,-1,1,3,\ldots \}$ 。這些是部分，例如， $S_{1}$ 是奇數。

}}定理等價關係在基礎集合上產生一個劃分。

證明

將集合稱為 $S$ ，關係稱為 $R$ 。根據上段的說明，對於每個 $x\in S$ ，定義 $S_{x}=\{y\,{\big |}\,(x,y)\in R\}$ .

觀察到，由於 $x$ 是 $S_{x}$ 的一個成員，所有這些集合的並集是 $S$ 。因此，如果我們能證明不同的部分是不相交的，那麼我們就完成了：如果 $S_{x}\neq S_{y}$ ，那麼 $S_{x}\cap S_{y}=\varnothing$ 。我們將透過逆否命題來驗證這一點，也就是說，我們將假設 $S_{x}\cap S_{y}\neq \varnothing$ ，以便推匯出 $S_{x}=S_{y}$ .

設 $p$ 是交集中的一個元素。根據 $S_{x}$ 和 $S_{y}$ 的定義，這兩個 $(x,p)$ 和 $(y,p)$ 是 $R$ 的成員，並且由於這種關係的對稱性， $(p,x)$ 和 $(p,y)$ 也是 $R$ 的成員。為了證明 $S_{x}=S_{y}$ ，我們將證明每個集合都是另一個集合的子集。

假設 $q\in S_{x}$ ，使得 $(q,x)\in R$ 。使用傳遞性以及 $(x,p)\in R$ 可以得出結論： $(q,p)$ 也是 $R$ 的元素。但是 $(p,y)\in R$ ，因此傳遞性的另一個應用表明 $(q,y)\in R$ 。因此 $q\in S_{y}$ 。所以 $q\in S_{x}$ 意味著 $q\in S_{y}$ ，因此 $S_{x}\subseteq S_{y}$ .