電子材料/波粒二象性/雙縫實驗/理想

實驗裝置

雙縫實驗在理論上非常容易設定，它展示了波的一些非常有趣的特性，即使在量子物理之外也是如此。一個相干的單色波源被指向一塊不透明屏上的兩個縫隙。由於縫隙會衍射波，這將產生兩個密切相關的光源

• 它們都具有相同的波長（因為原始光源是單色的）
• 它們都是相干的（波處於相位）

這在下面的圖中以概念形式顯示。這是一個非常簡單的圖表，但它有助於描述這個概念。

現在讓我們為設定指定一些引數。我們將使用光源（如雷射）產生波，其波長為 800nm。這正好位於可見光譜的紅色端之外，人眼幾乎看不到。然而，這是一個方便使用的數字，因為它很容易被除。如果你在現實生活中做這個實驗，光很可能是大約 700nm（深紅色）。我們將讓我們的光穿過兩個縫隙（我們假設這些縫隙非常窄，以至於衍射是完美的），間距為 0.1mm，正如我們將看到的，這會產生顯著的效果，並且在實踐中並不難實現。然後我們將我們的螢幕放置在距離縫隙 5 米的地方。所以，我們的引數是

• $\lambda =400\times 10^{-9}{\mbox{ m}}\,$
• $d=0.1\times 10^{-3}{\mbox{ m}}\,$
• $L=5{\mbox{ m}}\,$

假設我們的介質的折射率非常接近 1（如空氣），我們也知道波速 c，因為這是一個普遍的常數

• $c=3\times 10^{8}{\mbox{ m s}}^{-1}$

因此我們可以計算出頻率 f 和角頻率 ω

• $f={\frac {c}{\lambda }}=375\times 10^{12}{\mbox{ Hz}}$
• $\omega =2\pi f=750\pi \times 10^{12}{\mbox{ rad s}}^{-1}$

也可以找到波數（每米的週期數） k

• $k={\frac {2\pi }{\lambda }}=2.5\pi \times 10^{6}{\mbox{ m}}^{-1}$.

單縫方程

讓我們首先考慮從一個縫隙發出的波。如果我們假設縫隙非常長（是波長的很多倍）並且非常窄（遠小於波長），並且雷射發出的光是平面波（因此縫隙上每個點的相位都相同），那麼我們可以說衍射波是圓柱形的

這可以透過波動方程直接證明。這意味著我們只需要考慮波前的“切片”，而不必擔心垂直距離的影響（即縫隙方向），因為它不會影響波。在現實生活中，雷射會產生一個緊密的亮點，因此產生的波是一個非常薄的圓柱形波（因為它沒有被長縫隙垂直衍射）。

現在讓我們考慮行波的方程。波在距離源 x 處和時間 t 處產生的擾動 u 由以下方程給出

$u\left(x,t\right)=A\left(x,t\right)\sin \left(kx-\omega t+\phi \right)$

其中 φ 是相位偏移量，從這裡開始我們可以將其設定為零，因為我們處理的所有波都是同相的。A(x,t) 是波的振幅包絡。為簡單起見，我們假設波在這個實驗中不會明顯衰減。這是一個可以接受的簡化，因為我們只關心波的相位關係。在現實生活中，圓柱形波的振幅與距離成反比（而不是球形波的距離平方）。

下面是在一個週期內一維行波的圖。此波不會隨著距離而衰減。

一維行波。您可以看到波在正 x 方向傳播

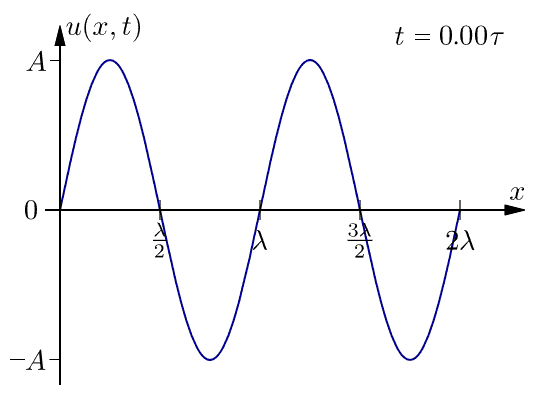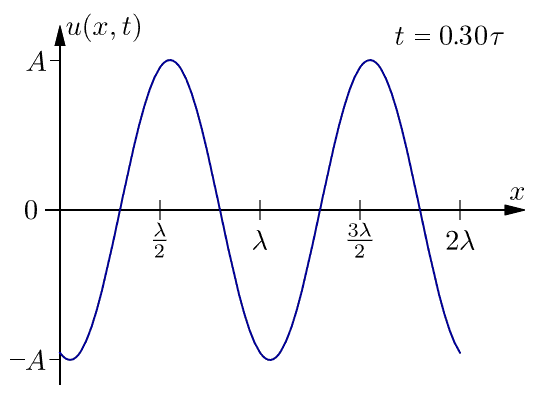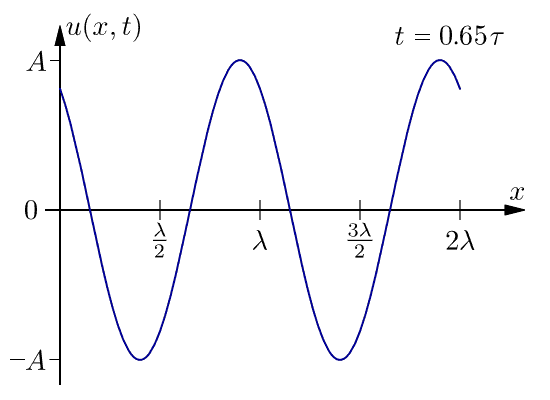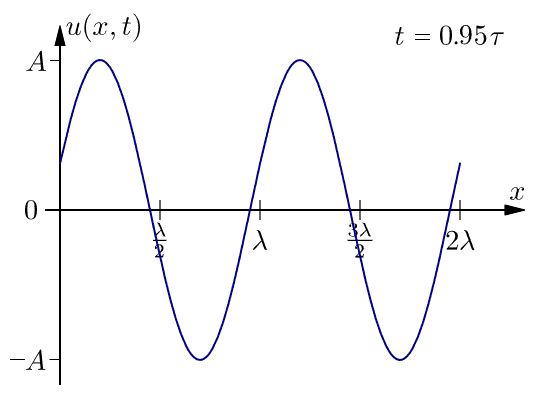
現在，由於我們知道我們正在處理圓柱形波，我們只需要考慮整個系統的二維切片。我們將 x 和 y 軸設定為與頁面頂部的影像中所示相同。在這種情況下，到 (x,y) 處的點的距離 r 由勾股定理給出

$r={\sqrt {x^{2}+y^{2}}}$

因此，我們二維空間中行波的方程式現在是（記住我們忽略了振幅和相位偏移）：

$u\left(x,y,t\right)=\sin \left(k{\sqrt {x^{2}+y^{2}}}-\omega t\right)$

下圖顯示了這個波在 t=0 時的樣子。注意這個波在原點是不光滑的（你可以看到一個翻轉過來的 - 實際上是相位差 180° - 的函式版本，這裡）。如果這個波被動畫化，它看起來像是向外流動。

我們可以使用以下公式，將其中一個點源定位在任意點 (x₀,y₀) 上：

$u\left(x,y,t\right)=\sin \left(k{\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}-\omega t\right)$

實驗模型

現在我們可以構建我們的雙縫實驗模型。如果我們將光源放置在 $\left(\pm {\frac {d}{2}},0\right)$，我們就得到了我們想要的縫隙間距 d。因此，空間和時間中任意點的擾動公式由以下公式給出：

$u(x,y,t)=\sin \left(k{\sqrt {\left(x-{\frac {d}{2}}\right)^{2}+y^{2}}}-\omega t\right)+\sin \left(k{\sqrt {\left(x+{\frac {d}{2}}\right)^{2}+y^{2}}}-\omega t\right)$

我們的縫隙間距為 0.1mm，波長為 800nm。這意味著縫隙相隔 125 個波長，因此我們可以在一個合理大小的圖表上很容易地識別出衍射圖案。下面是我們的裝置中衍射圖案的密度圖。黑色對應於最小振幅，白色對應於最大振幅，而中灰色對應於零振幅。我們現在只關注 y 值為正的情況，因為帶有縫隙的螢幕在 y=0 處形成屏障。

我們可以清楚地看到交叉的圖案，但我們無法直接看到任何“條紋”效應。這是因為條紋是波的平均值隨位置變化的結果。事實上，影像中確實包含了條紋的微弱證據。你可能會注意到，波中有大約是徑向的“帶”，它們從白色變為黑色，然後再變回白色，還有一些帶則保持在中灰色左右。這些帶會隨著時間保持在固定位置。跨越影像的帶是波的週期性和行進性質的產物，這些帶會隨著時間推移而移動。當波在一段時間內平均後，條紋就會變得清晰可見。下圖顯示了同一區域的圖，但與 b 中時間凍結的波不同，這個圖是由波在時間上的多個樣本組合而成的。亮區對應於合成的波振幅較高的位置，而黑區對應于波振幅為零的位置。

你可以在這裡看到條紋，但它們非常靠近，肉眼無法輕易識別。此外，條紋也不是完美的徑向（從單點發出），因此我們無法輕易確定它們的間距，除非繪製這個圖。如果我們從更遠的地方觀察這個系統（如之前一樣平均），我們就可以看到一個更簡單的圖案：

合成的波現在看起來像是一系列從縫隙發出（在這個尺度下縫隙不可見地分開）的徑向線，這些線交替出現高低強度。正如我們在下一節中發現的那樣，這使得一個非常有用的近似值是準確的。此外，條紋的間距也大得多，因此我們可以更容易地測量條紋間距。注意圖的左下角的明顯曲線 - 這裡沒有曲線，但規則的畫素網格與傾斜的線結合在一起，會導致出現虛假圖案。有關相關現象的更多資訊，請參閱 莫爾紋 和 外差和拍頻。

我們可以繪製一個 y=5m 處的波的圖。下圖是中央極大值，跨越一個波週期：

你無法在現實生活中看到這種振盪，因為可見光的頻率極高（數百太赫茲）。然而，我們可以感知螢幕上的輻照度。（有關推導，請參閱此頁面。現在，螢幕上某一點的輻照度 I 由以下公式給出：

$I=\epsilon v\langle \mathbf {E} ^{2}\rangle$

其中$\langle \mathbf {E} ^{2}\rangle$表示電場強度平方的時間平均值。這是場論的基本結果，這裡不作證明。目前，由於我們正在處理相對強度，我們將省略常數並設定

$I=\langle \mathbf {E} ^{2}\rangle$

根據疊加原理，

$\mathbf {E} =\mathbf {E} _{1}+\mathbf {E} _{2}$

其中E₁和E₂是由每個狹縫產生的場的分量。現在我們可以寫

$\mathbf {E} ^{2}=\left(\mathbf {E} _{1}+\mathbf {E} _{2}\right)^{2}$

$\mathbf {E} ^{2}=\mathbf {E} _{1}^{2}+\mathbf {E} _{2}^{2}+2\mathbf {E} _{1}+\mathbf {E} _{2}$

對該方程兩邊進行時間平均，得到

下圖是 t=0 時中心的 5 個極大值。您可以輕鬆地看到波幅值高的規則極大值，以及波幅值非常小的極小值。您還應該能夠看到強度變化類似於餘弦波的絕對值。

您可以將此與現實生活中看到的條紋進行比較（上面的圖案來自兩個狹縫，下面的圖案來自五個狹縫）

現在讓我們找到系統物理屬性和條紋間距之間的關係。

條紋間距的近似值

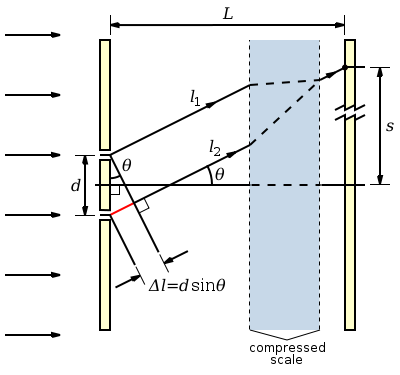
如果我們進行一些近似，就可以很容易地找到該系統中條紋間距的表示式。考慮右側的圖。它顯示了兩條光線，一條來自每個狹縫，都到達螢幕上的同一個點，用黑點標記。因為到螢幕的距離遠大於狹縫之間的距離，所以這些光線實際上是平行的。

現在，下方的光線比上面的光線走得更遠，我們將路徑長度差稱為Δl。這在圖中用紅色標記。對於完全的相長干涉，路徑差必須是波長的整數倍

$\Delta l=n\lambda ,\quad n=(0,1,2,\ldots )$

因為光線是平行的，所以我們可以看到標記為θ的兩個角度是相同的。這意味著我們可以使用三角函式從角度到點的距離來確定路徑差

$\sin \theta ={\frac {\Delta l}{d}}$

我們還可以使用θ來計算點到螢幕中心的距離s

$\tan \theta ={\frac {s}{L}}$

對於小角度，我們可以進行以下近似

$\sin \theta \approx \tan \theta$.

因此，我們可以寫

${\frac {\Delta l}{d}}={\frac {s}{L}}$

並將我們的最大相長干涉值代入，我們得到從中心線到第n個亮條紋的距離表示式

${\frac {n\lambda }{d}}={\frac {s}{L}}$

經過重新排列，得到

$s={\frac {n\lambda L}{d}},\quad n=(0,1,2,\ldots )$

讓我們用前面理論中的例子來試一下。要找到基本條紋間距，只需將n設為1（這是中心條紋和一側第一個條紋之間的間距）。

$s={\frac {\lambda L}{d}}$

$s={\frac {800\times 10^{-9}\times 5}{0.1\times 10^{-3}}}$

$s=0.04{\mbox{ m}}\,$

這與我們觀察到的幾乎完全一致（它只是一個近似值，所以技術上不完全精確）。為了使該公式有效，以下條件必須成立：

• 從狹縫到螢幕的距離 *L* 必須遠大於狹縫間距 *d*。
• 從狹縫到條紋的角度 *θ* 必須很小。
• 如前所述，狹縫必須足夠窄，以實現近乎完美的衍射。