化學/三角學數學

三角學 - 正弦和餘弦規則

三角形

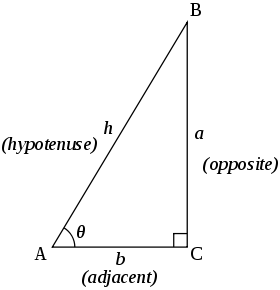
在以下三角恆等式中，$a$，$b$ 和 $c$ 是三角形中對應角 $A$，$B$ 和 $C$ 對邊的長度。

• 正弦定理 ${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}$
• 餘弦定理 $c^{2}=a^{2}+b^{2}-2ab\cos C$
• 比率恆等式 $\tan A={\frac {\sin A}{\cos A}}$

三角恆等式

$\cos ^{2}\theta +\sin ^{2}\theta =1$

請記住，這是畢達哥拉斯定理的結果，其中斜邊的長度為 1。

$\sin(\theta +\phi )=\sin \theta \cos \phi +\cos \theta \sin \phi$

$\cos(\theta +\phi )=\cos \theta \cos \phi -\sin \theta \sin \phi$

兩個角度的差可以透過將 $\phi =-\phi$代入並記住 $\sin -\phi =-\sin \phi$ 和 $\cos -\phi =\cos \phi$來輕鬆生成。類似地，倍角公式可以透過歸納法生成。 $\tan(\theta +\phi )$稍微複雜一些，但如果你能處理分數，就可以生成它！證明過程可以在許多教科書中找到，但作為化學家，沒有必要知道它們，只需要知道結果即可。

恆等式和方程

恆等式和方程看起來非常相似，都是由一個等號連線的兩個事物。然而，恆等式是數學等價性的記憶輔助工具，可以被證明。方程代表關於某個情況的新資訊，可以被求解。

例如，

$\cos ^{2}\theta +\sin ^{2}\theta =1$

是一個恆等式。它不能被求解 $\theta$；它對所有 $\theta$ 都成立。然而，

$\cos ^{2}\theta =1$

是一個方程，其中 $\theta =\arccos \pm 1$.

如果你嘗試將一個恆等式作為方程求解，你會陷入迴圈，毫無進展，但你可以將 $\cos ^{2}\theta +\sin ^{2}\theta =1$ 轉換成一個非常複雜的表示式，你可能會把它誤認為是一個方程。

關於三角形的幾個觀察

檢查你是否熟悉基本的幾何知識。從你的 GCSE 數學中記住等邊三角形和等腰三角形的性質。如果你有一個等腰三角形，你總是可以省略正弦定理和餘弦定理，從底邊垂下一條垂直線，直接使用三角函式。記住，一條邊或一個角到頂點的角平分線將三角形按面積、角度和長度分成兩部分。這可以透過畫一個鈍角三角形來證明，可以看到面積是 ${\frac {1}{2}}{\frac {1}{2}}.R.h$.

多邊形的內角

記住，一個 $n$ 邊形的內角是 $180(n-2)$（以度為單位）或 ($n\pi -2\pi$)（以弧度為單位）。

對於 苯，如果將環的中心用作頂點，則有六個等邊三角形，每個三角形的內角為 120 度。假設所有 C-C 鍵長相等（這只是一個近似值），計算薁（一種具有五元環和七元環的烴）的角。