地球/1c. 測量地球的大小和形狀
大地測量學是準確測量和理解地球大小和形狀,以及地球在空間中的方位、旋轉和重力的科學。 大地測量學在為運輸、導航、建立國家和州界線以及房地產、土地所有權和管理地球表面資源而繪製地球表面地圖方面很重要。許多工業化國家的民眾都會在口袋裡攜帶一個極其精確的大地測量工具(智慧手機或平板電腦),直到最近美國軍方才允許民用使用 全球定位系統 (GPS)。 GPS 利用地球軌道衛星來準確地確定你在地球上的位置。 GPS 的最新進展使得從追蹤包裹、繪製遷徙動物的路線到設計自動駕駛汽車等一切變得可能。令人驚歎的是,在 1990 年代後期民用 GPS 地球軌道衛星出現之前,所有地圖繪製、追蹤和導航都是使用原始工具完成的。這些原始工具已經為地球的大小和形狀建立了相當準確的測量結果,持續了 2500 年之久。
由於地球繞其極軸自轉,太陽從東方升起,從西方落下,導致每個經度都有太陽在天空最高處的時間不同。學者們知道,如果一個人擁有一個精確的時鐘,它被設定為特定的中午時間,就可以計算出太陽在世界各地不同位置最高處時的時間差,並將其與時鐘上設定的標準時間進行比較。利用這個時間差,可以確定你與標準時間在經度上的距離,這個標準時間被稱為 本初子午線。
如果你曾經乘坐飛機(或汽車)穿過 時區,並必須在抵達後將手錶設定為新的當地時間,你已經體驗過這種效應。原則上,你可以透過調整手錶多少小時來確定你在經度上的距離。雖然古代學者沒有精確的時鐘來準確地確定經度,但他們試圖盡他們所能確定經度,以生成一個網格系統,該系統將緯度和經度覆蓋在一個球體上。
最早的將地球描述為球體的文字可以追溯到 埃利亞的巴門尼德 的著作,他生活在今天的義大利南部,一個名為 韋利亞 的福基斯希臘殖民地。這些著作,主要是希臘詩歌,描述了宇宙是一個球形的月亮繞著一個球形的地球執行,可以追溯到公元前 535 年左右。 地中海 的水手們可能已經從對大型水體上船隻的觀察中瞭解到地球的曲率。當船隻在公海航行越來越遠時,它們似乎會沉入地平線以下。月亮和它在天空中出現的月相也暗示了月亮和地球的球形性質,以及日食和月食的記錄,當球形的月亮或地球阻擋太陽的光線時。沒有記錄表明這些早期航海者以及其他航海者計算過地球的周長或半徑,但他們可能在探索公海時發現了地球的球形性質。
埃拉託斯特尼 出生在非洲北部海岸,大約在公元前 276 年,在希臘雅典接受教育後,被任命為 埃及亞歷山大 的首席圖書館員。 亞歷山大圖書館 由 托勒密一世 建立,他是 亞歷山大大帝 的同伴,在征服埃及後成為埃及的統治者。該圖書館是學習和教育的中心,收藏著當時希臘和埃及作品。 埃拉託斯特尼 能夠充分利用這個教育中心的優勢,並且寫得非常出色,儘管不幸的是,他的著作中只有很少一部分流傳至今。希臘學者 克利奧梅德 幾個世紀後寫的一本教科書描述了 埃拉託斯特尼 進行的著名實驗。
在一個叫做 象島 的小島上,它位於現在的 阿斯旺 附近, 尼羅河 中間,有一口水井,在一年中最長的一天,太陽會直接照射到黑暗的水井中,照射到水面上。在很短的時間內,太陽的反射光完美地位於井的中心。埃拉託斯特尼好奇的是,在距離 象島 北部約 524 英里的 亞歷山大 是否也會發生同樣的事情。 埃拉託斯特尼 沒有挖井,而是豎起一根杆子(或者更技術地說,一根 圭表,它是一根投射陰影的杆子),完全垂直於地面,並在一年中最長的一天,當太陽在 亞歷山大 達到最高點時,觀察太陽在地面上的影子。在 亞歷山大,陽光照射到垂直的 圭表 或杆子上,即使在正午也會產生陰影。 埃拉託斯特尼 測量了陰影的最小長度,注意到太陽在南部的 象島 正 overhead,而在北部的 亞歷山大 稍微 overhead 的差別,可能是由於地球的曲率造成的。
埃拉託斯特尼 還意識到,如果太陽離地球非常遠,並且陽光平行於地球表面傳播,他可以使用陰影的長度來計算地球沿著南北軸的周長。他知道 亞歷山大 和 象島 之間的距離為 5000 斯塔迪亞,這是一個隨著時間推移而消失的度量單位,但大約相當於 524 英里(843 公里)。埃拉託斯特尼計算出從地球中心的角度大約是 1/50(7.2 度),這意味著從極點到極點的子午線周長為 26200 英里(42165 公里),這與我們現代計算的 周長 24860 英里(40008 公里) 非常接近。 埃拉託斯特尼 還意識到,透過測量棍子上的陰影長度,可以推斷出你位於哪個方向的北或南。越往北走,陰影就越長。陰影長度也取決於一年中的時間,可以使用太陽曆進行修正,例如,埃拉託斯特尼在每年的每一天都測量了標準長度的 圭表 或杆子在亞歷山大的最小正午陰影長度。旅行者可以攜帶一根類似的標準長度的圭表或杆子,測量陰影的長度,並將它與在 亞歷山大 測量的當天陰影進行比較。這將告訴旅行者他們距離 亞歷山大 的北部或南部有多遠。
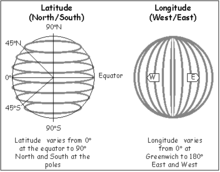
埃拉托色尼 發現了地球的大小和形狀,還發現了這種驚人的方法來確定緯度。就像爬梯子一樣,緯度 是指從兩極之間南北方向的度數測量值,其中 赤道,即地球上距離兩極等距的中間帶,位於 0 度,而兩極分別位於北緯 90 度和南緯 90 度。 埃拉托色尼 通常被認為是 地理學 的鼻祖,地理學是研究地球上地點和自然特徵排列的學科。

請注意,埃及的象島非常靠近 北迴歸線,這是地球上最北端的緯度圈,在 6 月 (夏季) Solstice 或北半球一年中最長的那一天的中午時分,太陽直射這裡。地球上還有一個緯度圈叫做 南迴歸線,它是地球上最南端的緯度圈,在 12 月 (冬季) Solstice 的中午時分,太陽可以直射這裡。這是因為地球相對於其軌道平面傾斜了 23.5 度。

在船舶上使用陰影投射技術並不奏效,因為在水上搖晃會導致陰影投射不準確。為了在海上確定緯度,水手會使用夜空,測量北極星 (北極星) 在地平線上的仰角,並將該角度與當年的星圖進行比較。
公元 500 年左右,印度數學家 阿耶波多 在印度進行了創新,他計算了 π (π) 的無理數性質,從而打開了利用三角學計算地球周長的途徑。 阿耶波多 的數學被翻譯成阿拉伯語,並被早期的穆斯林學者使用,特別是 穆罕默德·伊本·穆薩·花拉子米 (拉丁語稱作演算法學家) 是 巴格達智慧之屋 的首席圖書管理員。他發表了許多關於各個城市和地點位置的巧妙計算。為了確定緯度,他使用了一種比陰影投射更簡單的方法。他會使用 鉛垂線(一根系著重物的繩子) 進行測量,並測量從山峰或山頂到遠處觀測到的地平線的角度。如果你知道這個距離,這個角度可以告訴你山頂和地平線點之間的度數,你就可以更準確地計算地球的周長。雖然這允許更精確地測量 地球的子午線周長,但它仍然不能提供測量 地球的赤道周長 的方法。學者們假設地球是一個完美的球體,赤道周長和子午線周長相等,但赤道周長尚未確定。確定你沿著東西軸的位置特別困難。 穆罕默德·伊本·穆薩·花拉子米 發明了代數,以及在 xy 網格系統中定位一組數字的方法。雖然到目前為止確定任何城市的緯度都相當簡單,但確定經度或東西方向卻很成問題。 托勒密,一位比他早八個世紀的希臘學者,曾試圖繪製 地中海 地圖,但未能確定沿著東西軸的距離,並且高估了地中海的長度。 穆罕默德·伊本·穆薩·花拉子米 開始嘗試確定所有主要城市的位置的緯度和經度,在他的《地球描述書》中,該書於公元 833 年用阿拉伯語出版。
確定經度的不準確性導致了 1492 年地理學上最嚴重的誤解之一。 克里斯托弗·哥倫布 從西班牙穿越 大西洋 的探險是一次大膽的嘗試,他相信自己會到達大洋另一邊的印度或亞洲。當他的探險隊發現了陸地 (伊斯帕尼奧拉島) 時,他確信他們已經到達了印度,因為他無法準確地確定自己的經度位置。1499 年,阿隆索·德·奧赫達,哥倫布探險隊中的一名成員,帶領自己的隊伍再次穿越大西洋,並帶上了義大利學者 阿美利哥·維斯普奇,後者在船上試圖繪製這些新發現的土地地圖。探險隊沿著現在 委內瑞拉 和 巴西 的海岸線向南行駛,到達了 亞馬遜河 的河口。 維斯普奇 在沿途記錄了緯度,並且驚奇地發現夜空中出現了南部的星座,這些星座他只在書本中讀到過。他測量的緯度讓他離 赤道 只有 6 度,比預期的要遠得多,如果這片土地是 印度,那就更不可能了。他急於嘗試使用月亮和火星來測量經度的位置。 維斯普奇 帶有火星在夜空中相對於月亮的位置的圖表,這些圖表是在 歐洲 製作的,並且記錄了火星被月亮遮擋的年份。他測量了這些夜晚月亮遮擋火星時月亮和火星之間的距離,在 歐洲 可以看到這些夜晚,但在船上卻可以看到。透過測量圖表中記錄的那些日期月亮和火星之間的距離,他可以估計他們位置的經度,並意識到他們並不靠近印度,而是發現了一塊大型大陸,延伸到很遠的南方。1507 年,德國地圖繪製者 馬丁·瓦爾德澤米勒 將這塊新大陸命名為美洲,以紀念 阿美利哥·維斯普奇 在世界上第一張精確地圖《宇宙地圖》中發現的這塊大陸。

對經度的更準確估計是必要的,特別是在 1500 年至 1700 年間水手更加頻繁地航行世界各地以及歐洲早期對美洲的殖民時期。君主們為任何能夠準確地確定經度的科學家提供了鉅額資金, 羅伯特·胡克,皇家學會 的創始成員之一,試圖設計一個彈簧鍾或使用擺來測量時間,從而確定經度。 約翰·哈里森 是一位經驗豐富的鐘表匠,他設計了第一個真正精確的時鐘,或 航海天文鐘,到 1761 年,這些天文鐘可以被用來非常準確地確定經度。

航海時鐘或稱為航海天文鐘會設定為格林威治標準時間 (GMT),其中正午或下午 12:00 設定為英國格林威治的皇家天文臺觀察到太陽位於天空最高點的時間。英國格林威治被設定為 0 度經度,因此被稱為本初子午線。水手們可以透過觀察航海天文鐘,當太陽位於天空最高點時,讀取設定為GMT的時間,從而輕鬆地確定自己的經度。顯示的時間表明你距離本初子午線有多遠,是位於東邊還是西邊。
緯度和經度使用四邊形度數進行測量,分為 60 分和 60 秒。例如,緯度為北緯 40°27′19″,經度為西經 109°31′43″。表示一個地方位於赤道的北邊 40 度 27 分 19 秒,以及英國格林威治本初子午線的西邊 109 度 31 分 43 秒。
在現代使用中,緯度和經度通常以小數格式給出,例如 40.45552° 和 −109.52875°,其中正緯度表示北半球,負緯度表示南半球,而負經度表示本初子午線的西邊,正經度表示本初子午線的東邊。地球表面的任何地方都可以用這兩個簡單的數字來描述。事實上,你可以將任何小數緯度和經度複製貼上到 WolframAlpha 的查詢框中,並在地圖上找到它的位置。
使用精確的緯度和經度,地球的子午線周長為 24,860 英里(40,007.86 公里),而地球的赤道周長為 24,901 英里(40,075.017 公里),表明赤道附近有一個 67.157 公里的輕微隆起,所以它不是一個完美的球體,而是一個輕微的扁球體。
雖然知道緯度和經度很重要,但對於日常旅行者來說,確定地球上兩點之間的距離是一個更重要的概念。早期的航海家透過三角測量原理開發了許多技術。三角測量是透過形成已知點的三角形來確定位置的過程。在古代猶他州和整個美國西南部,古代普韋布洛人在沙漠中建造了塔樓,這些塔樓用火點燃。旅行者可以透過測量兩點之間的角度(例如在晚上觀察到的燃燒的火),並確定前往目的地的方向和距離來導航。由於緯度和經度的誤差,早期海上航海家使用沿海岸線上的燈塔進行三角測量,以幫助他們將危險的海岸線導航到安全的海灣和安全的港口,因為他們的航行估計存在偏差。在中國,三角測量被用來確定城市之間的距離以及山脈的高度。
三角測量透過測量已知距離的兩點之間以及遠處未知點之間的角度,或測量從一個點到另兩點之間視線的距離(從該距離可以測量出視線與原始起點的角度),來進行。這些角度使用三角表達式表示,需要你瞭解兩個角度和一個距離,才能計算出第三個距離。三角測量需要視線,並且在視野沒有太多遮擋的沙漠環境中效果最佳。在樹木茂密的森林或開闊的海面上,由於地平線上可觀測到的物體很少,因此很難進行三角測量。三角測量被用來繪製大陸內部的大部分割槽域,透過從海岸線城市或重要城市中心(這些城市已經確定了準確的緯度和經度)開始的一系列測量網路進行。
三角測量的概念在太空時代將成為確定地球大小和形狀的一個非常重要的概念,因為地球軌道衛星可以用來非常準確地測量地球上任何點的緯度和經度,並以極高的確定性測量距離和海拔高度。多邊定位不是測量角度,而是使用三維空間中的距離來找到一個點,該點位於三個球體的交點,其中三個球體的半徑距離是已知的。

1957 年 10 月 4 日,蘇聯成功發射了斯普特尼克 1 號,這是人類設計的第一顆衛星,直徑近 2 英尺(58.5 釐米),進入地球軌道。斯普特尼克 1 號的設計很簡單,是一個球體,但它會發射兩種可以在地球上接收到的無線電頻率。根據發射的無線電頻率,可以透過多普勒效應確定衛星的位置。多普勒效應是指當波的頻率發生變化時,取決於物體的運動方向。當斯普特尼克朝一個地方移動時,地球上的無線電接收器會檢測到更高的頻率,而當斯普特尼克遠離一個地方移動時,無線電接收器會檢測到更低的頻率。任何擁有無線電接收器的人都可以確定斯普特尼克何時直接位於頭頂,因為由於多普勒效應,無線電頻率會改變音調。

檢測斯普特尼克發射的無線電頻率,使地球上任何無線電接收站都可以知道其相對於發射無線電波的軌道衛星的位置。這使得可以更準確地確定地球上的點的位置。在接下來的幾十年裡,許多衛星被髮射到太空,並被放置在地球軌道上。這些早期衛星中的大多數會發射無線電訊號,這些訊號可以在地球表面接收。就像三角測量一樣,如果你在某個位置上方有至少三顆衛星,接收器可以根據來自太空的三顆或更多顆衛星發射的無線電訊號的距離對其位置進行三角測量。
這些早期衛星的一個驚人的突破是,它可以對地球上任何位置相對於地球中心的位置進行詳細測量,從而實現了高度測量,即測量某個位置相對於地球中心的距離,而不是相對於海平面的距離。這種創新使得可以更精確地測量地球表面的地形。海平面會隨著每日和每月潮汐的漲落而上下波動,因此它不是一個很好的基準線,人們使用了地球尺寸的各種數學模型。

當斯普特尼克第一次繞地球軌道執行時,格拉迪斯·韋斯特,一位年輕的非裔美國數學家,在美國弗吉尼亞州的達爾格倫海軍基地工作,她參與了對早期大型計算機的程式設計,用於計算火箭彈道。隨著斯普特尼克的出現,美國軍方很快意識到衛星資料在確定導彈彈道和使用遠端火箭方面的重要性。格拉迪斯·韋斯特是一位精通數學的數學家,在 1980 年代,海軍給了她一個看似不可能的任務,即使用新發射的GEOSAT 衛星的衛星資料來確定海面地形。這意味著要將三角測量改進到如此精確的程度,以至於可以透過高度測量來測量任何船隻在航行海洋時遇到的海浪和潮汐的高度。韋斯特設計了一種數學校正系統,使海洋和陸地的表面地形可以與一個稱為大地水準面的參考橢球體進行比較。大地水準面是地球的純粹數學模型,沒有其不規則的地形,最常用的模型是世界大地測量系統 (WGS84),然而,在用於美國大陸地圖的兩個較早的大地水準面模型中,經常使用1927 年北美大地測量基準 (NAD27)和1983 年北美大地測量基準 (NAD83),這兩個模型在北美之間的差異可能高達 95 到 47 米,並且是基於 1866 年首次為製圖目的而開發的模型。它們略有不同,因為它們對地球赤道隆起進行建模的方式不同。
世界大地測量系統 (WGS84)是用於全球應用的更好的大地水準面,被廣泛用作國際標準。格拉迪斯·韋斯特開發了一個數學模型來消除誤差,使精確的動態海面地形以及緯度和經度可以在 1980 年代的船舶計算機上計算出來。這項創新導致瞭如今大多數手機、船舶和車輛中使用的 GPS 導航的使用。
如今,許多繞地球執行的衛星並非透過傳送無線電波並利用多普勒效應計算距離來工作,而是透過從機載高精度原子鐘發射帶有時間戳的無線電波來工作。每顆衛星發射無線電波,傳輸其當前的廣播時間,當接收無線電波時,將時間與另一臺機載原子鐘進行比較,兩者的時間差就是無線電波以光速傳播到接收機所需的時間。至少有 3 顆衛星發射訊號,就可以確定每顆衛星的位置,但為了更精確,通常會使用 4 顆或更多顆發射衛星來建立它們彼此之間的相對位置,以提高精度。使用 GPS 接收器,可以利用來自 4 顆或更多顆衛星的無線電發射球形波來找到地球上任何位置的精確位置。使用接收器進行三角測量的衛星越多,位置就越精確。由於地球自轉改變了地球上的位置,因此相對於軌道上可見衛星的數量也會發生變化。
美國 GPS (全球定位系統) 導航衛星是一個網路或星座,大約有 33 顆衛星在地球軌道上執行,每顆衛星都向地球提供即時訊號,用於高精度計算地球上的任何位置。其他國家開發了五個其他衛星網路,包括由俄羅斯維護的 GLONASS 網路,由 歐盟 維護的 伽利略網路,由中國維護的 北斗網路,以及印度和日本分別計劃維護的 IRNSS 和 QZSS。
現在,對於固定在地面的 GPS 接收器來說,地球上任何位置的精度都已達到亞釐米級(小於一英寸)。這一技術突破使得以毫米級精度測量地球表面和地殼的運動成為可能。使用這項技術的更模糊的專案之一是 EarthScope,該專案從 2012 年執行到 2019 年,在整個美國大陸部署了數千個 GPS 接收站,以測量每個位置的地面運動。這些 GPS 接收器觀測到大陸板塊的運動,表明南加州下方的地面相對於美國大陸內陸(如猶他州)的相對快速運動(每年約 40 毫米)。這些 GPS 接收器還表明,由於月球的引力,地面每天上下垂直移動兩次,幅度為 55 釐米,而由於太陽的引力,地面上下垂直移動兩次,幅度為 15 釐米。因此,雖然您似乎生活在一個堅固不動的地面上,但它實際上每天都在動態地上下移動,因為堅固的內部在月球和太陽的執行過程中被拉伸,而水平方向上則因為地質板塊的移動而發生移動。
| 上一頁 | 當前頁 | 下一頁 | |
|---|---|---|---|
