訊號與系統/工程函式

訊號與系統

基本函式

通常，複雜的訊號可以簡化為某些基本函式的線性組合（傅立葉分析中的一個關鍵概念），這在工程領域很有用。這些函式將在本文件中進行描述，並在後續章節中進行更詳細的探討。

單位階躍函式

單位階躍函式和衝激函式被認為是工程學中的基本函式，強烈建議讀者熟悉這兩個函式。

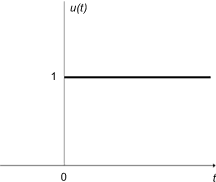單位階躍函式，也稱為Heaviside 函式，定義如下：

u(t)=\left\{{\begin{matrix}0,&{\mbox{if }}t<0\\1,&{\mbox{if }}t\geq 0\end{matrix}}\right.

有時，u(0) 會被賦予其他值，通常是 0 或 1。對於許多應用來說，零點處的取值無關緊要。u(0) 通常被寫為未定義。

導數

單位階躍函式在除 t = 0 處的間斷點外，所有地方都是水平的。因此，單位階躍函式的導數在所有點 t 處都為 0，除了 t = 0。在 t = 0 處，單位階躍函式的導數是無窮大。

單位階躍函式的導數稱為衝激函式。衝激函式將在下一節中更詳細地描述。

積分

單位階躍函式的積分計算如下：

\int _{-\infty }^{t}u(s)ds=\left\{{\begin{matrix}0,&{\mbox{if }}t<0\\\int _{0}^{t}ds=t,&{\mbox{if }}t\geq 0\end{matrix}}\right\}=tu(t)

換句話說，單位階躍函式的積分是一個“斜坡”函式。該函式對於所有小於零的值都為零，並且從零開始變成一條斜率為 +1 的直線。

時間反轉

如果我們要反轉單位階躍函式，我們可以像這樣將其繞著 y 軸翻轉：u(-t)。經過一些操作，我們可以得到一個重要的結果：

u(-t)=1-u(t)

, 同時

t\neq 0

其他屬性

這裡我們將列出單位階躍函式的一些其他屬性：

$u(\infty )=1$
$u(-\infty )=0$
$u(t)+u(-t)=1$ , 同時 $t\neq 0$

這些都是重要的結果，讀者應該熟悉它們。

衝激函式

衝激函式是一個特殊的函式，工程師經常用它來模擬某些事件。衝激函式是不可實現的，因為根據定義，衝激函式的輸出在某些值上是無窮大的。衝激函式也稱為“狄拉克函式”，儘管存在不同型別的狄拉克函式，它們各自具有略微不同的屬性。具體來說，這種單位衝激函式被稱為狄拉克 delta 函式。術語“衝激函式”是明確的，因為“衝激”一詞只有一個定義。

讓我們從繪製一個矩形函式 D(t) 開始，如下所示

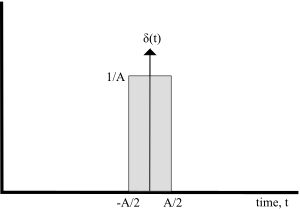
我們可以用單位階躍函式來定義這個矩形

D(t)={\frac {1}{A}}[u(t+A/2)-u(t-A/2)]

現在，我們想分析這個矩形，當 A 變得無窮小的時候。我們可以用這個矩形來定義這個新函式，即狄拉克函式

\delta (t)=\lim _{A\to 0}{\frac {1}{A}}[u(t+A/2)-u(t-A/2)]

我們可以用分段的方式類似地定義狄拉克函式，如下所示

$\delta (t)=0{\mbox{ for }}t\neq 0$ .
$\delta (t)=+\infty {\mbox{ for }}t=0$ .
$\int _{-\infty }^{\infty }\delta (t)dt=1$ .

雖然，這個定義不如之前的定義嚴謹。

積分

從它的定義可以得出，衝激函式的積分就是階躍函式

\int \delta (t)dt=u(t)

因此，將單位階躍函式的導數定義為衝激函式是合理的。

平移性質

此外，對於可積函式 f

\int _{-\infty }^{\infty }\delta (t-A)f(t)dt=f(A)

這被稱為狄拉克函式的平移性質（也稱為篩選性質或取樣性質）；它有效地對函式 f 在位置 A 處的值進行取樣。

狄拉克函式在工程中有很多應用，其中最重要的應用之一是將連續函式取樣為離散值。

利用這個性質，我們可以透過乘以一個衝激，然後積分，從連續函式中提取一個單一的值。

狄拉克函式的型別

有一些不同的函式都被稱為“狄拉克函式”。這些函式通常都像一個衝激，但有一些區別。一般來說，本書使用“狄拉克函式”一詞來指代狄拉克 delta 函式。

Sinc 函式

在通訊工程中，有一種形式出現得非常頻繁，因此我們給它起了一個自己的名字。這個函式叫做“Sinc 函式”，將在下面討論。

Sinc 函式定義如下

\operatorname {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}{\mbox{ if }}x\neq 0

和

\operatorname {sinc} (0)=1

sinc(x) 的值在 x = 0 處定義為 1，因為

\lim _{x\rightarrow 0}\operatorname {sinc} (x)=1

.

這個事實可以透過注意到 x 接近 0 時，

1>{\frac {\sin {(x)}}{x}}>\cos {(x)}

.

由於 cos(0) = 1，我們可以應用夾逼定理來證明當 x 趨近於零時，sinc 函式趨近於 1。因此，將 sinc(0) 定義為 1 使 sinc 函式連續。

此外，當 x 趨近於無窮大時，Sinc 函式趨近於零，且 sinc(x) 的包絡以 1/x 的速度衰減。

矩形函式

矩形函式是一個產生以 t = 0 為中心，寬度為 1 的矩形脈衝的函式。矩形脈衝的高度也為 1。Sinc 函式和矩形函式構成傅立葉變換對。

矩形函式可以寫成以下形式

\operatorname {rect} \left({\frac {t-X}{Y}}\right)

其中，脈衝以 X 為中心，寬度為 Y。我們可以透過將脈衝中心設定為零 (X = 0)，高度設定為 1/A，寬度設定為 A（趨近於零）來根據矩形函式定義上面的衝激函式

\delta (t)=\lim _{A\to 0}{\frac {1}{A}}\operatorname {rect} \left({\frac {t-0}{A}}\right)

我們也可以用一對單位階躍函式構造矩形函式

\operatorname {rect} \left({\frac {t-X}{Y}}\right)=u(t-X+Y/2)-u(t-X-Y/2)

在這裡，兩個單位階躍函式都設定在距 (t - X) 中心點 Y/2 的距離處。

方波

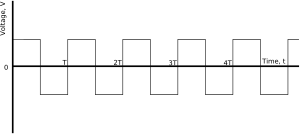
方波是一系列矩形脈衝。以下是一些方波的示例


這兩個方波具有相同的幅度，但第二個方波的頻率較低。我們可以看到，第二個方波的週期大約是第一個方波的兩倍，因此第二個方波的頻率大約是第一個方波頻率的一半。


這兩個方波具有相同的頻率和相同的峰峰值幅度，但第二個方波沒有直流偏移。請注意，第二個方波以x軸為中心，而第一個方波完全位於x軸上方。