訊號與系統/Z 變換簡介

取樣系統

數字訊號本質上是取樣訊號。在電路節點中，數字以給定的速率變化：取樣速率或取樣頻率。訊號兩次變化之間的時間是取樣頻率的倒數：它是取樣週期。

在處理器系統中，樣本儲存在記憶體中。在邏輯電路中，它們對應於暫存器輸出。取樣週期用於計算系統中所有訊號的下一個值。

數位電路不是唯一的取樣系統：諸如開關電容濾波器之類的類比電路也依賴於開關，因此也被取樣。

對訊號進行取樣

奈奎斯特速率

對訊號進行取樣提出了一個主要問題：在這個過程中是否會丟失資訊？

例子

例子：每小時檢查（=取樣）一次交通訊號燈肯定會讓人對它們的訊號反應遲鈍（=丟失資訊）。

另一方面，每微秒取樣一次交通訊號燈並不會比每毫秒取樣一次帶來更多資訊。

顯然，交通訊號燈，像任何其他訊號一樣，必須以比其變化更快的速率進行取樣，但以更快的速率取樣它們並不會帶來更多資訊。

奈奎斯特速率 是為了避免資訊丟失而所需的最低取樣速率。

$f_{N}\ {\stackrel {\mathrm {def} }{=}}\ 2f_{b}$

其中 $f_{b}$ 是要取樣的訊號的最高頻率，也稱為頻寬。

為了避免丟失資訊，取樣速率必須高於奈奎斯特速率

$f_{s}>f_{N}$

在實踐中，取樣速率是透過一定的裕量來確定的，以便更輕鬆地重建原始訊號。

例子

例子：音訊內容取樣速率

人類聽覺的全部範圍在 20 赫茲到 20 千赫茲之間。因此，音訊內容必須以超過 40 千赫茲的速率進行取樣。

事實上

• CD 音訊以 44.1 千赫茲的速率對訊號進行取樣。
• 專業數字影片裝置以 48 千赫茲的速率對它們進行取樣。
• DVD 音訊以 96 千赫茲的速率對它們進行取樣。
• 高階 DVD 音訊將該頻率翻倍至 192 千赫茲。

混疊

以低於奈奎斯特速率的速率對訊號進行取樣會產生混疊 或摺疊。

混疊的影響。

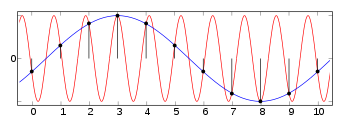
右圖顯示了一個頻率為 0.9（因此週期接近 1.1）的紅色正弦波。此訊號應該以高於 1.8 的頻率進行取樣。但是，訊號是以 1 的速率進行取樣的（垂直線和黑點）。如果嘗試在樣本之間繪製一條線，結果將看起來像藍色曲線，該曲線是週期為 10 或頻率為 0.1 的正弦波。

如果訊號以 0.9 的速率進行取樣，取樣點將始終落在正弦函式中的同一點，並且生成的訊號將看起來像一個常數。

以 1 的速率對頻率為 0.9 的訊號進行取樣會建立一個頻率為 $1-0.9=0.1$ 的混疊。

以 0.9 的速率對頻率為 0.9 的訊號進行取樣會建立一個直流混疊，因此頻率為 $0.9-0.9=0$。

以 0.8 的速率對頻率為 0.9 的訊號進行取樣也會建立一個頻率為 $0.9-0.8=0.1$ 的混疊，但相位不同。

例子

例子：頻閃燈是一個眾所周知的混疊例子。

用以 100 赫茲頻率切換的頻閃燈照亮一個以 90 赫茲頻率旋轉的電機，會讓我們覺得它以 100 赫茲 - 90 赫茲 = 10 赫茲的頻率旋轉。

用以 90 赫茲頻率切換的頻閃燈照亮一個以 90 赫茲頻率旋轉的電機，會讓我們覺得它靜止不動。

用以 80 赫茲頻率切換的頻閃燈照亮一個以 90 赫茲頻率旋轉的電機，會讓我們覺得它以 90 赫茲 - 80 赫茲 = 10 赫茲的頻率旋轉，但方向相反。

這與許多美國西部電影中出現的驛馬車場景中看到的現象相同。在不同的旋轉速度下，驛馬車上的車輪看起來會向前旋轉、靜止不動或向後旋轉。參見 車輪效應。

就好像訊號的頻譜在等於取樣頻率一半的點處被摺疊回去了。

欠取樣

以低於奈奎斯特速率的頻率進行取樣，也稱為欠取樣，會在較低的頻率處建立正弦波混疊。如果原始訊號在這些較低的頻率處也存在內容，那麼它們將混合在一起，並且會丟失資訊。

但是，如果訊號只包含高頻內容，那麼欠取樣過程會以較低的頻率對訊號進行調製。

這是一種使用乘以調製正弦波的方式進行調製的廉價替代方案。

過取樣

過取樣對應於以遠高於奈奎斯特頻率（通常為奈奎斯特頻率的 100 到 1000 倍）進行取樣。過取樣的目的是能夠用更少的位數來表示訊號。

這可以透過用於恢復額外位的機制來解釋：只要新的取樣頻率大於奈奎斯特頻率，以 10 kHz 取樣的訊號就可以以 5 kHz 進行降取樣。降取樣意味著樣本數量減少一半。而不是丟棄每隔一個樣本，可以計算兩個連續樣本的平均值，並使用該結果來構建新訊號的一個樣本。計算平均值對應於將值相加併除以二。而不是將結果除以二並丟棄小數點後的位，可以僅將連續樣本兩兩相加。這樣，5 kHz 訊號的幅度是原始 10 kHz 訊號的兩倍。換句話說，它需要用多 1 位來表示。

過取樣一個廣泛應用的應用是 脈衝寬度調製 (PWM)。調製訊號用一個以 ${2^{n}}\cdot f_{N}$ 頻率切換的單個位表示，其中 $f_{N}$ 是原始訊號的奈奎斯特頻率，而 $n$ 是用於表示它的位數。這個單位元訊號非常適合用單個電源開關驅動大電流負載。PWM 通常用於驅動電動機。

在每個 CD 播放機中都可以找到一個用於單位元結果的更復雜的編碼方案：Σ-Δ 調製。理解它的工作原理需要更多的理論知識。我們只說明它能夠在比 PWM 更低的取樣頻率下用單個位表示訊號。另一方面，單位元訊號在它的取樣頻率下更頻繁地來回切換，因此不適合驅動較慢的大電流開關。Σ-Δ 調製用於驅動更輕的負載，例如 CD 播放機和音訊放大器之間的電纜。

例子

示例：超級音訊光碟 (SACD)

SACD 以 直接流數字 訊號的形式對音訊進行編碼，該訊號以單個位編碼，是 CD 44.1 kHz 取樣率的 64 倍。

Z 變換

Z 變換 用於表示取樣訊號和 線性時不變 (LTI) 系統（例如濾波器），類似於拉普拉斯變換表示連續時間訊號。

訊號表示

Z 變換 用於表示取樣訊號，類似於拉普拉斯變換表示連續時間訊號。

取樣訊號由它的樣本之和給出，每個樣本都延遲了取樣週期的不同倍數。拉普拉斯變換表示一個取樣週期的延遲 $T_{s}$ 為

$z^{-1}{\stackrel {\mathrm {def} }{=}}e^{-sT_{s}}$

有了這個，Z 變換可以表示為

$X(z)={\mathcal {Z}}\{x[n]\}=\sum _{n=0}^{\infty }x[n]z^{-n}$

其中 $x[n]$ 是取樣訊號的連續值。

線性時不變系統

連續時間線性時不變 (LTI) 系統可以用傳遞函式來表示，該傳遞函式是復變數 $s$ 的兩個多項式的分數。

$H(s)={\frac {num(s)}{den(s)}}$

它們的頻率響應透過取 $s=j\omega$ 來估計，即透過估計傳遞函式沿虛軸的值。

為了確保穩定性，傳遞函式的極點（分母多項式的根）必須位於 $s$ 的左半平面。

Z 平面單位圓

離散時間線性時不變 (LTI) 系統可以用兩個關於復變數 $z$的多項式的比值來表示。

$H(z)={\frac {num(z)}{den(z)}}$

根據定義

$z{\stackrel {\mathrm {def} }{=}}e^{sT_{s}}$

我們可以發現，它們的頻率響應可以透過取 $z=e^{j\omega T_{s}}$來估計，這相當於在單位圓上估計傳遞函式。

為了保證穩定性，傳遞函式的極點（分母多項式的根）必須位於單位圓內。

傳遞函式的週期性

傳遞函式是在單位圓上估計的。

• 座標為 $z=1+j0$的點對應於頻率 $f=0$，也就是直流分量。
• 座標為 $z=0+j1$的點對應於頻率 $f=f_{s}/4$，即取樣頻率的四分之一。
• 座標為 $z=-1+j0$的點對應於頻率 $f=f_{s}/2$，即取樣頻率的一半。
• 座標為 $z=0-j1$的點對應於頻率 $f=3f_{s}/4$。
• 座標為 $z=1+j0$的點對應於頻率 $f=f_{s}$，也就是取樣頻率。

因此，繞單位圓旋轉一週後，就會回到起點 $z=1+j0$。從那裡，可以從 $f_{s}$ 旋轉到 $2f_{s}$，再從 $2f_{s}$ 旋轉到 $3f_{s}$，等等... 在每次旋轉中，頻率響應都將相同。換句話說，取樣系統的傳遞函式是週期性的，週期等於取樣頻率。

對於實數（而不是複數）訊號，傳遞函式在取樣頻率的一半處是對稱的：$f=f_{s}/2$。因此，取樣系統的傳遞函式通常只考慮在 $f=0$ 和 $f=f_{s}/2$ 之間。