狹義相對論/數學方法2

四維向量

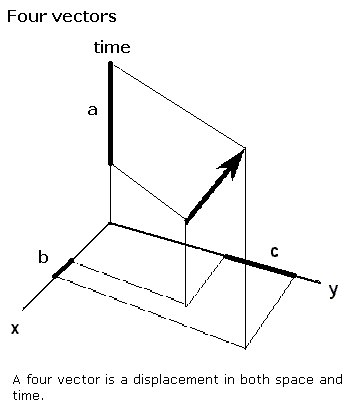
四維向量表示時空中的位移。

如果時空的度規由以下給出

$ds^{2}=dt^{2}-dx^{2}-dy^{2}-dz^{2}$

並且如果時空是平坦的，則四維向量的模可以透過以下公式計算

$\mathbf {S} ^{2}=A^{2}-B^{2}-C^{2}-D^{2}$

其中 A，B，C，D 是向量在對應座標軸 (t,x,y,z) 上的投影。四維向量的模由以下公式給出

$S=|\mathbf {S} ^{2}|^{1/2}={\sqrt {A^{2}-B^{2}-C^{2}-D^{2}}}$

四維向量的標量積（也稱為“點積”或“內積”）可以像普通向量（三維向量，參見 標量積）一樣推導。因此，兩個四維向量 $\mathbf {A.B}$ 的標量積是

$\mathbf {A.B} =A_{t}B_{t}-A_{x}B_{x}-A_{y}B_{y}-A_{z}B_{z}$

這也可以很容易地從閔可夫斯基時空的度規張量中推匯出來。兩個四維向量 x 和 y 的標量積定義（使用指標記號）為

$x\cdot y=x^{a}\eta _{ab}y^{b}=\left({\begin{matrix}x^{0}&x^{1}&x^{2}&x^{3}\end{matrix}}\right)\left({\begin{matrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}}\right)\left({\begin{matrix}y^{0}\\y^{1}\\y^{2}\\y^{3}\end{matrix}}\right)=-x^{0}y^{0}+x^{1}y^{1}+x^{2}y^{2}+x^{3}y^{3}$

四維向量的標量積與座標系無關

${\begin{matrix}A'_{x}&=&\gamma \left(A_{x}-{\frac {v}{c}}A_{t}\right)\\A'_{y}&=&A_{y}\\A'_{z}&=&A_{z}\\A'_{t}&=&\gamma \left(-{\frac {v}{c}}A_{x}+A_{t}\right)\end{matrix}}$

在這個參考系中，標量積為

${\underline {A'}}\cdot {\underline {B'}}=A'_{x}B'_{x}+A'_{y}B'_{y}+A'_{z}B'_{z}-A'_{t}B'_{t}$

簡化後，我們得到

${\begin{matrix}{\underline {A'}}\cdot {\underline {B'}}&=&\gamma ^{2}\left(A_{x}B_{x}-{\frac {v}{c}}(A_{x}B_{t}+A_{t}B_{x})+{\frac {v^{2}}{c^{2}}}A_{t}B_{t}\right)\\&&+A_{y}B_{y}+A_{z}B_{z}&\\&&-\gamma ^{2}\left({\frac {v^{2}}{c^{2}}}A_{x}B_{x}-{\frac {v}{c}}(A_{x}B_{t}+A_{t}B_{x})+A_{t}B_{t}\right)\\&=&\left(1-{\frac {v^{2}}{c^{2}}}\right)^{-1}\left(A_{x}B_{x}+{\frac {v^{2}}{c^{2}}}A_{t}B_{t}\right)\\&&+A_{y}B_{y}+A_{z}B_{z}\\&&-\left(1-{\frac {v^{2}}{c^{2}}}\right)^{-1}\left({\frac {v^{2}}{c^{2}}}A_{x}B_{x}-A_{t}B_{t}\right)\\&=&A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}-A_{t}B_{t}\end{matrix}}$

這與原始參考系中的標量積相同。

屬性

1. 對向量加法的分配律 $\mathbf {A} .(\mathbf {B} +\mathbf {C} )$

2. 對稱性 $\mathbf {A.B} =\mathbf {B.A}$

3. 萊布尼茨微分法則適用，即：$d(\mathbf {A.B} )=d\mathbf {A} .\mathbf {B} +\mathbf {A} .d\mathbf {B}$

4. 正交性 $\mathbf {A.B} =0$ 如果 $\mathbf {A}$ 垂直於 $\mathbf {B}$

5. $\mathbf {A.A} =\mathbf {A} ^{2}$

我們現在知道兩個四維向量的點積是一個標量結果，即它的值與座標系無關。這在某些情況下可以被利用。

在時空的奇異幾何中，垂直的含義並不明顯。因此，我們定義兩個四維向量 ${\underline {A}}$ 和 ${\underline {B}}$ 是垂直的，如果它們的點積為零，與三維向量相同。

${\underline {A}}\cdot {\underline {B}}=0$

因為點積是一個標量，如果向量在一個座標系中是垂直的，它們在所有座標系中都是垂直的。

我們也可以考慮一個四維向量 ${\underline {A}}$ 的點積，它在未加標註的座標系中分解為 $(A_{x},A_{t})$。讓我們進一步假設在某個加標註的座標系中，類空間分量為零，因此該座標系中的分量為 (0, A_t' )。點積與座標系無關這一事實意味著

${\underline {A}}\cdot {\underline {A}}=A_{x}^{2}-A_{t}^{2}=-A_{t}'^{2}$

這構成了將時空勾股定理擴充套件到除位置四維向量之外的其他四維向量。因此，例如，某個波的波數在加標註的座標系中可能為零，這意味著未加標註的座標系中的波數和頻率與加標註的座標系中的頻率的關係為 $k^{2}-\omega ^{2}/c^{2}=-\omega '^{2}/c^{2}$.

我們用下劃線表示四維向量，並將分量寫成以下形式：${\underline {k}}=(k,\omega /c)$，其中 ${\underline {k}}$ 是波的四維向量，$k$ 是其空間分量，$\omega /c$ 是其時間分量。對於三維空間，我們有一個波向量而不是波數，我們寫成 ${\underline {k}}=(k,\omega /c)$。

另一個四維向量的例子是時空中的位置向量，${\underline {x}}=(x,ct)$，或者在三維空間中為${\underline {x}}=(\mathbf {x} ,ct)$。在這個例子中，$c$ 乘以時間分量，這是為了使其與空間分量具有相同的維度。

固有時間

在經典力學中，時間導數 d/dt 就像一個標量，所以我們可以用它乘以一個向量，得到另一個向量。

在相對論中，t 是一個四維向量的一部分，這意味著 d/dt 也是，所以我們不能簡單地用 t 對向量進行微分並期望得到向量。

例如，一個靜止粒子的位置是 (0, ct)。

從一個以速度 v 向右移動的參考系來看，它的位置變為 (-vτ, cτ)，其中 τ=γt 是在移動參考系中測量的時 間。

如果我們對 τ 進行微分，速度將為 (-v, c)

如果我們對 t 進行微分，在靜止參考系中得到 (0, c)，如果這是一個四維向量，那麼在移動參考系中將得到 (使用洛倫茲變換) (-γv, -γc)。

這兩個表示式在同一參考系中測量時相差一個因子 γ，因此這不能是一個四維向量。

然而，如果移動的觀察者除以 γ（即時間膨脹），他們將得到與靜止觀察者相同的向量。

這樣做相當於用粒子自身靜止參考系中的時間進行微分。由於這對位置向量有效，我們可以預期它對所有向量都有效。

在粒子靜止參考系中測量的時 間稱為其固有時間。

用固有時間對向量進行微分得到另一個向量，這是時間導數的相對論等價物。