狹義相對論/數學變換

在本科物理課程中教授狹義相對論需要相當的數學背景知識。特別重要的是向量和矩陣的操作以及對曲率的初步瞭解。本節末尾給出了數學背景，可以供不熟悉這些技術的人參考。

洛倫茲變換

洛倫茲變換處理的是相對運動的觀察者。一個觀察者記錄的事件座標與另一個觀察者記錄的事件座標之間是如何相關的？洛倫茲變換計算中使用的標準配置如下所示

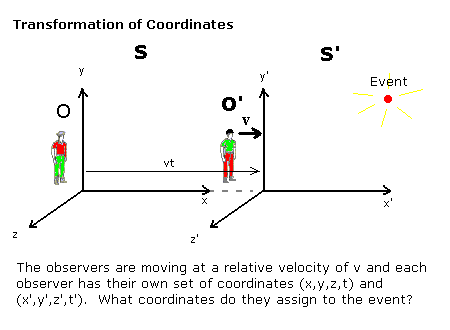
推匯出洛倫茲變換的方法有很多。通常的方法是從愛因斯坦的假設（物理定律在所有慣性參考系中都是相同的，光速是常數）開始，同時加上關於各向同性、線性和平移性的假設。另一種方法是從四維閔可夫斯基度量的假設開始。

在數學中，變換通常用“對映到”符號來表示

$(x,y,z,t)\mapsto (x^{'},y^{'},z^{'},t^{'})$

時空的線性和齊次性

考慮一個自由運動的時鐘。根據牛頓第一定律，物體在不受力的情況下將保持勻速直線運動；因此，時鐘在任何給定方向上的速度 ($dx_{i}/dt$) 必須是一個常數。

如果時鐘是一個真實的時鐘，其讀數由 $\tau$ 給出，那麼在任何其他慣性參考系中，相對於這些讀數的經過時間變化率 ($dt/d\tau$) 將是一個常數。如果時鐘相對於其他時鐘以不均勻的速率滴答作響，那麼宇宙在時間上就不是齊次的——在某些時候，時鐘似乎會加速。這也意味著牛頓第一定律將被打破，宇宙在空間上就不是齊次的。

如果 $dx_{i}/dt$ 和 $dt/d\tau$ 是常數，那麼 $dx_{\mu }/d\tau \,(\mu =1,2,3,4)$ 也是常數。這意味著時鐘沒有加速，即 $d^{2}x_{\mu }/d\tau ^{2}=0$.

線性體現在事物的長度與位置或相對位置無關；例如，如果$x'=ax^{2}$，兩點之間的距離將取決於觀察者的位置，而如果關係是線性的（$x'=ax$），則分離與位置無關。

線性性和齊次性假設意味著$S'$慣性系中物體的座標與$S$慣性系中的座標之間的關係為

$x_{\nu }'=(\sum \Lambda _{\nu \mu }x_{\mu })+B_{\nu }$

此公式稱為龐加萊變換。它可以用指標符號表示為

$x^{'\nu }=\Lambda _{\mu }^{\nu }x^{\mu }+B^{\nu }$

如果兩個參考系的原點重合，那麼可以假設$B_{\nu }$為零，方程

$x_{\nu }'=\sum \Lambda _{\nu \mu }x_{\mu }$

不熟悉此符號的人應注意，符號$x_{1}$等表示$x_{1}=x$，$x_{2}=y$，$x_{3}=z$和$x_{4}=t$，因此上面的方程是以下內容的簡寫

$x'=a_{11}x+a_{12}y+a_{13}z+a_{14}t$

$y'=a_{21}x+a_{22}y+a_{23}z+a_{24}t$

$z'=a_{31}x+a_{32}y+a_{33}z+a_{34}t$

$t'=a_{41}x+a_{42}y+a_{43}z+a_{44}t$

使用矩陣表示法，可以將這組方程寫成：

$\mathbf {x'} =\mathbf {\Lambda x}$

標準配置（見上圖）具有幾個特性，例如：

兩個觀察者座標系的空間原點都位於運動線上，因此可以將 x 軸選為平行。

由 $x=vt$ 給出的點與 $x'=0$ 是相同的。

兩個座標系的原點可以重合，這樣當它們彼此相鄰時，時鐘就可以同步。

座標平面 ,y, y' 和 z,z' 可以排列成與運動方向正交（成直角）。

各向同性意味著在一個座標系中 y=0 和 z=0 時正交的座標平面，在另一個座標系中 y'=0 和 z'=0 時也是正交的。

根據相對性原理，任何兩個相同慣性參考系之間的變換都必須相同。這被稱為互易定理。

洛倫茲變換

從線性假設出發，考慮到原點 $y=0=y^{'}$，因此沒有常數偏移，那麼 $y^{'}=Ky$ 和 $y=Ky^{'}$，因此 K=1。所以

$y^{'}=y$

以及，透過相同的推理

$z^{'}=z$

現在，考慮到事件的 x 座標，可以假設 z 軸和 y 軸為 0（即：座標的任意偏移，允許事件位於 x 軸上）。如果這樣做，那麼線性考慮和 $x=vt$ 和 $x^{'}=0$ 是同一點，可以得出

(1) $x^{'}=\gamma (x-vt)$

其中 $\gamma$ 是一個常數。根據互易定理，我們也有

(2) $x=\gamma (x^{'}+vt^{'})$

現在可以引入愛因斯坦關於光速恆定的假設，使得 $x=ct$，也使得 $x^{'}=ct^{'}$。所以

$ct^{'}=\gamma t(c-v)$

以及

$ct=\gamma t^{'}(c+v)$

所以

$c^{2}tt^{'}=\gamma ^{2}tt^{'}(c^{2}-v^{2})$

以及

$\mathbf {\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}}$

因此，洛倫茲變換方程為

$t^{'}=\gamma (t-vx/c^{2})$

$x^{'}=\gamma (x-vt)$

$y^{'}=y$

$z^{'}=z$

時間座標的變換可以從 x 座標的變換推匯出，假設 $x=ct$ 以及 $x^{'}=ct^{'}$，或者直接從方程式 (1) 和 (2) 中透過類似的替換獲得 $x=ct$。

洛倫茲變換的係數可以用矩陣形式表示

${\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\gamma &-{\frac {v}{c}}\gamma &0&0\\-{\frac {v}{c}}\gamma &\gamma &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}ct\\x\\y\\z\end{bmatrix}}.$

這種由於運動引起的座標變換被稱為boost。

洛倫茲變換方程可以用來證明

$c^{2}dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}$

儘管在推匯出洛倫茲變換時，線性、各向同性及均勻性假設是否從一開始就假設了這個恆等式，是一個有爭議的問題。

鑑於：$c^{2}dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}$ 也等於 $c^{2}dt^{''2}-dx^{''2}-dy^{''2}-dz^{''2}$，以及其他一系列連續的變換，我們可以清楚地看到

$\mathbf {\Delta s} ^{2}=c^{2}\Delta {t}^{2}-\Delta {x}^{2}-\Delta {y}^{2}-\Delta {z}^{2}$

量 $\Delta s$ 被稱為時空間隔，量 $\mathbf {\Delta s} ^{2}$ 被稱為位移平方。

對於所有觀察者而言，給定的位移平方都是恆定的，無論他們以多快的速度運動，它被稱為不變。

方程

$ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}$

被稱為時空的度量。

另一種看待洛倫茲變換的方式

我們已經瞭解到長度和持續時間對於移動的觀察者看起來是不同的

• 長度在同時測量時，會縮短 γ 倍。
• 持續時間在同一地點測量時，會縮短 γ 倍。

我們可以擴充套件這些結果，以允許在不同時間和地點進行測量。

讓我們考慮兩個觀察者 O 和 O'，O' 相對於 O 沿 x 軸以速度 v 運動。我們將使用帶撇號的變數來表示 O' 進行的所有測量。

目前我們可以假設這兩個觀察者具有相同的原點和 x 軸，因為我們已經知道如何允許觀察者相對旋轉和平移。稍後我們可以將這些複雜情況放回。

現在，任何長度或持續時間都可以寫成兩個座標之間的差值，即物體兩端或事件開始和結束的座標差值，因此只需知道如何將座標從一個座標系轉換為另一個座標系就足夠了。

我們知道如何在經典物理學中做到這一點，

${\begin{matrix}x'&=&x-vt\\t'&=&t\end{matrix}}$

我們需要將其擴充套件到相對論。

請注意，在經典物理學中，這種關係是線性的；這些方程的影像為直線。這使得數學運算變得簡單得多，因此我們將嘗試在相對論中找到座標之間的線性關係，即一般形式為

${\begin{matrix}x'&=&mx+nt\\t'&=&px+qt\end{matrix}}$

其中 m、n、p 和 q 均與座標無關。

首先，我們知道

• 當 t=0 時，x′ = γx（洛倫茲收縮）
• 當 x=0 時，t′ = γt（時間膨脹）

並且 O' 以速度 v 運動。他們測量自己的位置為 x′=0，但 O 測量的位置為 vt，因此我們必須有

當 x-vt=0 時，x′=0

x 和 x′ 之間唯一滿足這些條件的關係為

$x'=\gamma (x-vt)\,$

這兩個觀察者必須測量光速相同，

$x=ct\Rightarrow x'=ct'\,$

或者，代入並整理，

$x=ct\Rightarrow t'=\gamma {\frac {x-vt}{c}}$

滿足這些條件的唯一t和t′之間的線性關係是

$t'=\gamma (-{\frac {vx}{c^{2}}}+t)\,$

因此，帶撇號和不帶撇號的座標透過以下關係式關聯

${\begin{matrix}x'&=&\gamma (x-vt)\\t'&=&\gamma \left(-{\frac {vx}{c^{2}}}+t\right)\end{matrix}}$

這些方程被稱為洛倫茲變換。

如果我們用ct而不是t來寫，它們看起來會更簡單。

${\begin{matrix}x'&=&\gamma \left(x-{\frac {v}{c}}ct\right)\\ct'&=&\gamma \left(-{\frac {v}{c}}x+ct\right)\end{matrix}}$

以這種方式寫出來，它們看起來很像描述三維空間中旋轉的方程。事實上，一旦我們允許不同的勾股定理，它們就與旋轉方程**完全相同**。

• 如果觀察者彼此相對運動，它們的座標系將在(x,ct)平面上旋轉。

從第一個假設推匯出光速不變性

以下文字取自“華夏公益教科書”講座。

洛倫茲變換 可以僅從第一個假設推匯出，無需任何其他假設。

洛倫茲變換描述了當一個觀察者O2在一個不同的慣性系中看到一個向量時，一個觀察者O1看到的時空中的向量變化的方式。

狹義相對論的假設指出，物理定律與觀察者的速度無關。這等效於要求物理定律的數學表述必須在使用洛倫茲變換改變空間和時間的座標時保持不變。

這就是洛倫茲變換是狹義相對論中的核心概念的原因。

四維向量是指在進行洛倫茲變換後，表現得像來自時空的向量的向量。找到對應於非相對論定律的相對論定律的標準方法是找到四維向量來代替空間向量。令人驚訝的是，這種簡單的方法經常會成功。

為了簡單起見，這裡選擇了空間座標，使得x軸指向O2相對於O1運動的方向，而y和z座標沒有考慮在內。

這裡介紹了一種確定矩陣$L(v)$ 的方法，該矩陣將座標從O1變換到O2，其中v是O2相對於O1的速度。

一般來說，這個矩陣看起來像$L(v)=\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)$ 並將$\left({\begin{matrix}t\\x\end{matrix}}\right)$ 轉換到$\left({\begin{matrix}t^{\prime }\\x^{\prime }\end{matrix}}\right)$ 透過$\left({\begin{matrix}t'\\x'\end{matrix}}\right)=\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)\left({\begin{matrix}t\\x\end{matrix}}\right)$.

這個矩陣的第一個要求是 O2 將在其自身的座標系中靜止（在空間中）。

因此，對於任何時間 t，$\left({\begin{matrix}t'\\0\end{matrix}}\right)=\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)\left({\begin{matrix}t\\tv\end{matrix}}\right)$.

這給了我們$ct+tvd=0\Rightarrow c=-vd$ 和$L(v)=\left({\begin{matrix}a&b\\-vd&d\end{matrix}}\right)$.

從 O2 到 O1 的反向轉換由逆矩陣$L(v')=L(v)^{-1}=(\det(L(v))^{-1}\left({\begin{matrix}d&-b\\vd&a\end{matrix}}\right)$（其中$\,v'$ 是從 O2 看 O1 的速度）必須使 O1 在其自身的座標系中靜止。

假設 $v'=-v$（嚴格來說需要證明） 我們有 $\left({\begin{matrix}t\\0\end{matrix}}\right)=(\det(L(v))^{-1}\left({\begin{matrix}d&-b\\vd&a\end{matrix}}\right)\left({\begin{matrix}t'\\-t'v\end{matrix}}\right)$ 對於任何時間 $\,t'$，導致 $a=d\Rightarrow L(v)=\left({\begin{matrix}a&b\\-va&a\end{matrix}}\right)$.

係數是v的函式。對於所有v，變換都是可逆的，所以 $0\neq \det L(v)=a(v)^{2}+va(v)b(v)\Rightarrow a(v)\neq 0$.

對於v=0，L(v)是單位矩陣，因此b(0)=0。這允許我們重寫 $b(v)=-va(v)\varepsilon (v)$，其中 $\varepsilon (v)$ 是一個未知函式。

現在 $L(v)=a(v)\left({\begin{matrix}1&-v\varepsilon (v)\\-v&1\end{matrix}}\right)$.

現在對於每一個$v_{0},v_{1}$，存在一個速度$v_{2}$，使得$L(v_{0})L(v_{1})=L(v_{2})$。利用我們已經證明的內容，得到${\begin{aligned}L(v_{0})L(v_{1})&=a(v_{0})\left({\begin{matrix}1&-v_{0}\varepsilon (v_{0})\\-v_{0}&1\end{matrix}}\right)a(v_{1})\left({\begin{matrix}1&-v_{1}\varepsilon (v_{1})\\-v_{1}&1\end{matrix}}\right)\\&=a(v_{0})a(v_{1})\left({\begin{matrix}1+v_{0}v_{1}\varepsilon (v_{0})&-v_{1}\varepsilon (v_{1})-v_{0}\varepsilon (v_{0})\\-v_{0}-v_{1}&1+v_{0}v_{1}\varepsilon (v_{1})\end{matrix}}\right)\\&=a(v_{2})\left({\begin{matrix}1&-v_{2}\varepsilon (v_{2})\\-v_{2}&1\end{matrix}}\right)\\&=L(v_{2}).\end{aligned}}$

比較對角線元素，我們立刻可以發現$\varepsilon (v_{0})=\varepsilon (v_{1})$對於$v_{0},v_{1}$ 的任意值，因此$\varepsilon (v)=\operatorname {const.} =\varepsilon$。

利用這個，我們可以重寫$a(v_{0})a(v_{1})(1+v_{0}v_{1}\varepsilon )=a(v_{2})$ 和 $\,a(v_{0})a(v_{1})(-v_{0}-v_{1})=-v_{2}a(v_{2})$，分別比較索引為 *（1,1）* 和 *（2,1）* 的元素。將$a(v_{2})$ 代入得到

$(1)\ \ a(v_{0})a(v_{1})(-v_{0}-v_{1})=-v_{2}a(v_{0})a(v_{1})(1+v_{0}v_{1}\varepsilon )$

由此可得 $v_{2}={\frac {v_{0}+v_{1}}{1+v_{0}v_{1}\varepsilon }}$.

將此代入第一個方程，得到 $a(v_{0})a(v_{1})(1+v_{0}v_{1}\varepsilon )=a({\frac {v_{0}+v_{1}}{1+v_{0}v_{1}\varepsilon }})$.

當 $v:=v_{0}=-v_{1}$ 時，上式簡化為 $a(v)a(-v)(1-v^{2}\varepsilon )=a(0)=1$，因為 $\,L(0)$ 是單位矩陣。

令 $\varphi (x)=\varphi (-x)$ 為偶函式，$\psi (x)=-\psi (-x)$ 為奇函式，使得 $a(v)=e^{\varphi (v)+\psi (v)}$.

這給了我們 $e^{\varphi (v)+\psi (v)+\varphi (v)-\psi (v)-2\pi \operatorname {i} k}=(1-v^{2}\varepsilon )^{-1}$。取對數並簡化得到 $\varphi (v)=-{\frac {1}{2}}\ln(1-v^{2}\varepsilon )+\pi \operatorname {i} k$，由此我們得到 $a(v)=\pm {\frac {1}{\sqrt {(1-v^{2}\varepsilon )}}}e^{\psi (v)}$，其中任何奇函式 $\,\psi (-v)=-\psi (v)$。負號被 $\,a(0)=1$ 排除。

將 $\,a(v)$ 代入方程 (1) 驗證了該解，但留下了 $\psi (v_{0})+\psi (v_{1})=\psi ({\frac {v_{0}+v_{1}}{1+v_{0}v_{1}\varepsilon }})$。

為了證明 $\psi (v)\equiv 0$，我們在基礎系統和變換系統中都翻轉 x 軸方向。軸方向的選擇不應導致不同的結果。在翻轉的座標系中，洛倫茲變換的形式為 $L(v')=a(v')\left({\begin{matrix}1&-v'\varepsilon \\-v'&1\end{matrix}}\right)=a(-v)\left({\begin{matrix}1&v\varepsilon \\v&1\end{matrix}}\right)$，對於 $v'=-v$。

另一方面，我們可以透過對 $L(v)$ 使用座標變換來計算 $L(v')$。

$L(v')=\left({\begin{matrix}1&0\\0&-1\end{matrix}}\right)a(v)\left({\begin{matrix}1&v\varepsilon \\v&1\end{matrix}}\right)\left({\begin{matrix}1&0\\0&-1\end{matrix}}\right)=a(v)\left({\begin{matrix}1&-v\varepsilon \\-v&1\end{matrix}}\right)$，由此可得$\,a(-v)=a(v)$，因此$\,\psi (-v)=\psi (v)$。結合$\,\psi (-v)=-\psi (v)$，可得$\psi (v)\equiv 0$。

觀察L(v)的特徵向量，我們可以看到它們是$\left({\begin{matrix}1\\\pm {\frac {1}{\sqrt {\varepsilon }}}\end{matrix}}\right)$，與v無關。

這等同於一個變換不變的速度${\frac {1}{\sqrt {\varepsilon }}}=:c_{0}$，實驗表明它等於光速。總的來說，我們有

$L(v)={\frac {1}{\sqrt {1-{\frac {v^{2}}{c_{0}^{2}}}}}}\left({\begin{matrix}1&-{\frac {v}{c_{0}^{2}}}\\-v&1\end{matrix}}\right)$

注意，對於$\varepsilon =0$，我們將得到伽利略情況，沒有有限的不變速度。

值得注意的是，如果我們不是在(t, x)的時空平面上進行同樣的推導，而是在(x, y)的空間平面上進行，用斜率m=y/x代替速度v=x/t，除了透過計算之外，只通過實驗就能發現$\,\varepsilon =-1$，而L(m)只是在歐幾里得空間中的一個旋轉，沒有實值的特徵向量。

將此結果與之前提到的互易性、齊性和平移不變性假設進行比較是一個有趣的練習。洛倫茲變換矩陣形式中包含的線性方程是否從一開始就假設了一個特定的時空？

此外，重要的是要提到，行列式$\,\det L(v)=1$，與速度無關。這直接意味著時空體積是守恆的。

時空的幾何

狹義相對論使用一個“平坦”的四維閔可夫斯基空間，它是時空的一個例子。然而，這個空間與標準的三維歐幾里得空間非常相似，而且幸運的是，因此非常容易處理。

笛卡爾三維空間中的距離微分 (ds) 定義為

$ds^{2}=dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}$

其中 $(dx_{1},dx_{2},dx_{3})$ 是三個空間維度的微分。在狹義相對論的幾何學中，添加了第四維時間，單位為 c，因此距離微分的方程變為

$ds^{2}=dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}-c^{2}dt^{2}$

在許多情況下，將時間視為虛數可能很方便（例如，它可以簡化方程），在這種情況下，上面的方程中的 $t$ 被替換為 $i.t'$，度量變為

$ds^{2}=dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}+c^{2}(dt')^{2}$

注意，在這種情況下，ds 是距離，而不是間隔。在使用“虛數”時間時應謹慎，它不是現代相對論的一部分。Blandford 和 Thorne (2004) 在他們的“經典物理學應用”(http://www.pma.caltech.edu/Courses/ph136/yr2004/ ) 中，關於虛數時間寫道：“(i) 它隱藏了 Minkowski 時空的真實物理幾何形狀，(ii) 它不能以任何合理的方式擴充套件到平坦時空中非正交基，以及 (iii) 它不能以任何合理的方式擴充套件到廣義相對論中必須使用的曲線座標。”

如果我們將空間維度降至 2，以便我們可以在 3D 空間中表示物理學

$ds^{2}=dx_{1}^{2}+dx_{2}^{2}-c^{2}dt^{2}$

我們看到，諸如以光速運動的光之類的物體沿著雙錐

由方程定義

$ds^{2}=0=dx_{1}^{2}+dx_{2}^{2}-c^{2}dt^{2}$

或者

$dx_{1}^{2}+dx_{2}^{2}=c^{2}dt^{2}$

這是半徑為 $r=cdt$ 的圓的方程。以光速運動的物體的路徑被稱為**零測地線**。如果我們將上述方程擴充套件到三個空間維度，則零測地線是半徑 = 距離 = c×(±時間) 的連續同心球。

$ds^{2}=0=dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}-c^{2}dt^{2}$

$dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}=c^{2}dt^{2}$

這個零對偶錐代表了空間中一個點的“視線”。也就是說，當我們看向星星並說“我正在接收的來自那顆星星的光線是 X 年前的”，我們就是沿著這條視線在看：一條零測地線。我們正在看一個距離我們 $d={\sqrt {x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}}$ 米的事件，並且發生在 d/c 秒之前。 因此，零對偶錐也被稱為“光錐”。（下圖左下角的點代表恆星，原點代表觀察者，線代表零測地線“視線”。）

-t區域中的錐體是該點“接收”的資訊，而+t區域中的錐體是該點“傳送”的資訊。

長度收縮、時間膨脹和相位

考慮兩個處於標準配置的慣性系。在第二個慣性系中有一個以 v m/s 的速度運動的剛性杆。杆的長度由同時觀察杆端點的位置來確定 - 如果杆在運動，使用任何其他長度測量方法都是沒有意義的。與杆以相同速度運動的觀察者測量其“靜止長度”。沿 x 軸的座標的洛倫茲變換為

$x^{'}=\gamma (x-vt)$

假設杆兩端的座標，$x_{1},x_{2}$，是同時確定的（即：$t$ 是常數）

$(x_{1}^{'}-x_{2}^{'})=\gamma (x_{1}-x_{2})$

或者，使用 $L_{0}=(x_{1}^{'}-x_{2}^{'})$ 表示杆的靜止長度， $L=(x_{1}-x_{2})$ 表示看到杆以 v m/s 的速度飛過的觀察者測量的杆的長度

$\mathbf {L_{0}=\gamma L}$

或者，詳細說明 $\gamma$

$\mathbf {L={L_{0}}{\sqrt {1-v^{2}/c^{2}}}}$

換句話說，以速度 $v$ 運動的物體的長度在運動方向上收縮了一個因子 ${\sqrt {1-v^{2}/c^{2}}}$。

洛倫茲變換也影響著時鐘讀數的變化速率。時間的洛倫茲變換為

$t^{'}=\gamma (t-vx/c^{2})$

這個變換有兩個組成部分

$t^{'}=\gamma t-\gamma vx/c^{2}$

並且是直線圖（例如：$t^{'}=mt+c$）。

圖的斜率為$\gamma$ 所以

$\Delta t^{'}=\gamma \Delta t$

或者

$t_{1}^{'}-t_{2}^{'}=\gamma (t_{1}-t_{2})$

因此，如果$T_{0}$是靜止參考系中的時間間隔，$T$是運動參考系中的時間間隔，則運動參考系中的時鐘看起來會變慢。

$T=\gamma T_{0}$

或者，展開

$\mathbf {T={\frac {T_{0}}{\sqrt {1-v^{2}/c^{2}}}}}$

圖的截距是

$-\gamma vx/c^{2}$

這意味著如果在點$x$處的時鐘與在原點之間同步的時鐘進行比較，它將顯示$\gamma vx/c^{2}$秒的恆定時間差。這個量被稱為相對論相位差或“相位”。

相對論相位與長度收縮和時間膨脹的結果一樣重要。它是沿著運動方向同步於原點的時鐘隨著距離而不同步的量。相位影響除同步時鐘的點以及經過該點的無窮小 y 和 z 平面上的所有時鐘。其他所有地方的時鐘在兩個參考系之間將不同步。下圖顯示了相位的影響

如果每個慣性參考系由分佈在空間中的時鐘陣列組成，那麼這些時鐘將不同步，如上圖所示。

有趣的是，當考慮時間差時，相位項是如何抵消的。它抵消是因為相位項$x^{'}v/c^{2}$應用於在帶撇參考系中處於恆定位置的時鐘。時間的洛倫茲變換是

$t={\frac {t^{'}+(v/c^{2})x^{'}}{\sqrt {(1-v^{2}/c^{2})}}}\,$

兩個時間之間的差異是

$t_{1}-t_{2}={\frac {t_{1}^{'}+(v/c^{2})x^{'}-t_{2}^{'}-(v/c^{2})x^{'}}{\sqrt {(1-v^{2}/c^{2})}}}\,}$

需要注意的是，時鐘在其自身參考系中處於相同位置 $x^{'}$。

結果是

$t_{1}-t_{2}={\frac {t_{1}^{'}-t_{2}^{'}}{\sqrt {(1-v^{2}/c^{2})}}}\,$

其中相位項已抵消。

• 透過Ives-Stilwell實驗測量時間膨脹

雙曲幾何

在狹義相對論的平坦時空

$s^{2}=c^{2}t^{2}-x^{2}-y^{2}-z^{2}$

僅考慮x軸

$s^{2}=c^{2}t^{2}-x^{2}$

雙曲線的標準方程為

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

在時空的情況下

${\frac {(ct)^{2}}{s^{2}}}-{\frac {x^{2}}{s^{2}}}=1$

時空間隔將時空中的一個位置或事件與另一個位置或事件分開。因此，對於給定從一個位置到另一個位置的運動或給定參考系中的給定固定長度、給定時間間隔等，時空度量描述了一個雙曲空間。這個雙曲空間包含了所有觀察者對給定間隔所做的所有觀察的座標。

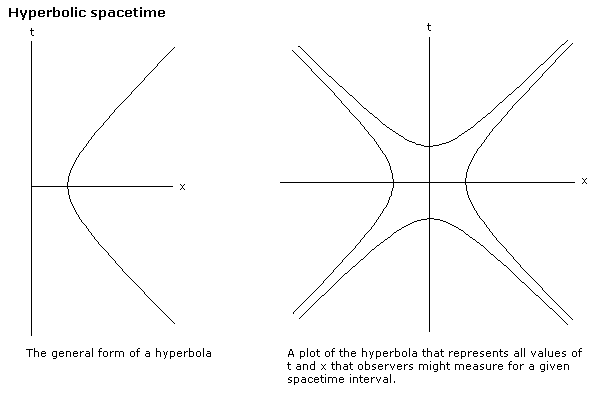
可以像在歐幾里得空間中一樣想象雙曲空間中的旋轉。雙曲空間中旋轉的概念總結在下圖中

雙曲空間中的旋轉等同於從一個參考系改變到另一個參考系，同時觀察相同的時空間隔。它正在從給出以下內容的座標移動

$(ct)^{2}-x^{2}=s^{2}$

到給出以下內容的座標

$(ct^{'})^{2}-{x^{'}}^{2}=s^{2}$

雙曲空間中旋轉的公式提供了洛倫茲變換的另一種形式，即

${\begin{bmatrix}ct\\x\end{bmatrix}}={\begin{bmatrix}\cosh \phi &\sinh \phi \\\sinh \phi &\cosh \phi \end{bmatrix}}{\begin{bmatrix}ct'\\x'\end{bmatrix}}.$

由此可得

$x=x^{'}\cosh \phi +ct^{'}\sinh \phi$

$ct=x^{'}\sinh \phi +ct^{'}\cosh \phi$

$\phi$ 的值可以透過考慮沿著 x 軸從原點以 $vmsec^{1}$ 運動的光的座標來確定，該光在 $t$ 秒內閃爍。

光上的觀察者分配的座標為：$t',0,0,0$，靜止觀察者分配的座標為 $t,x=vt,0,0$。下面是這些觀測結果的雙曲線圖

雙曲線的方程是

$(ct)^{2}-x^{2}=s^{2}=(ct^{'})^{2}$

但是，對於閃爍的結束，x=vt，因此

$\tanh \phi ={\frac {v}{c}}$

現在，從雙曲三角函式得到

${\frac {1}{\sqrt {1-\tanh ^{2}{\phi }}}}={\sqrt {\frac {\cosh ^{2}\phi }{\cosh ^{2}\phi -\sinh ^{2}\phi }}}=\cosh \phi$

但是 $\tanh \phi ={\frac {v}{c}}$，所以

$\cosh \phi ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}=\gamma$

並且，從雙曲三角函式公式 $\sinh \phi =\tanh \phi \cosh \phi$

$\sinh \phi ={\frac {v}{c}}\gamma$

將這些值代入雙曲旋轉方程

$x=x^{'}\cosh \phi +ct^{'}\sinh \phi$

$x=\gamma x^{'}+ct^{'}\gamma v/c$

給出 x 的標準變換。

$x=\gamma (x^{'}+vt^{'})$

類似地，$ct=x^{'}\sinh \phi +ct^{'}\cosh \phi$ 等同於

$t=\gamma (t^{'}+vx/c^{2})$

因此，洛倫茲變換也可以從假設提升等同於具有度量 $s^{2}=c^{2}t^{2}-x^{2}-y^{2}-z^{2}$ 的雙曲空間中的旋轉中推匯出。

雙曲角 $\phi$ 被稱為提升的快度。

速度的加法

假設有三個觀察者 1、2 和 3，它們沿 x 軸以不同的速度運動。觀察者 1 和 2 以相對速度 $v$ 運動，觀察者 2 和 3 以相對速度 $u^{'}$ 運動。問題是確定觀察者 3 由觀察者 1 觀測到的速度 ($u$）。

事實證明，快度之間存在一個非常方便的關係，可以解決這個問題。

如果 $v/c=\tanh {\phi }$ 並且 $u^{'}/c=\tanh {\alpha }$，那麼

$u/c=\tanh(\phi +\alpha )$

換句話說，快度可以簡單地從一個觀察者加到另一個觀察者，即

$\sigma =\phi +\alpha$

因此

$\tanh(\sigma )=\tanh(\phi +\alpha )$

所以速度可以透過簡單地新增快度來相加。使用雙曲三角函式

$u/c=\tanh(\alpha +\phi )={\frac {\tanh {\alpha }+\tanh {\phi }}{1+\tanh {\alpha }\tanh {\phi }}}={\frac {u^{'}/c+v/c}{1+u^{'}v/c^{2}}}$ 因此

$\mathbf {u={\frac {u^{'}+v}{1+u^{'}v/c^{2}}}}$

這就是相對論速度加法定理。

關係 $u/c=\tanh(\phi +\alpha )$ 如下所示

無需參考快度，就可以獲得速度變換。速度在任意方向上的變換的一般情況如下所述：

$\mathbf {u^{'}} =(u_{1}^{'},u_{2}^{'},u_{3}^{'})$

其中 $u_{1}^{'}$ 等是速度在 x、y、z 方向上的分量。

寫出速度的分量

$u_{1}^{'}=dx^{'}/dt^{'}$

$u_{2}^{'}=dy^{'}/dt^{'}$

$u_{3}^{'}=dz^{'}/dt^{'}$

但從洛倫茲變換中可以看出

$dx^{'}=\gamma (dx-vdt)$

$dy^{'}=dy$

$dz^{'}=dz$

$dt^{'}=\gamma (dt-vdx/c^{2})$

因此

$u_{1}^{'}=dx^{'}/dt^{'}={\frac {\gamma (dx-vdt)}{\gamma (dt-vdx/c^{2})}}$

$u_{2}^{'}=dy^{'}/dt^{'}={\frac {dy}{\gamma (dt-vdx/c^{2})}}$

$u_{3}^{'}=dz^{'}/dt^{'}={\frac {dz}{\gamma (dt-vdx/c^{2})}}$

將每個分數的分子和分母都除以$dt$

$u_{1}^{'}={\frac {\gamma (dx/dt-v)}{\gamma (1-vdx/dt/c^{2})}}$

$u_{2}^{'}={\frac {dy/dt}{\gamma (1-vdx/dt/c^{2})}}$

$u_{3}^{'}={\frac {dz/dt}{\gamma (1-vdx/dt/c^{2})}}$

將$\mathbf {u} =(u_{1},u_{2},u_{3})$代入

$u_{1}^{'}={\frac {u-v}{1-uv/c^{2}}}$

$u_{2}^{'}={\frac {u_{2}}{\gamma (1-uv/c^{2})}}$

$u_{3}^{'}={\frac {u_{3}}{\gamma (1-uv/c^{2})}}$

完整的速度變換如下表所示

${u^{'}}_{x}={\frac {(u_{x}-v)}{(1-u_{x}v/c^{2})}}$	$u_{x}={\frac {({u^{'}}_{x}+v)}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{y}={\frac {u_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{y}={\frac {{u^{'}}_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{z}={\frac {u_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{z}={\frac {{u^{'}}_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}$

計算完速度向量的分量後，現在可以計算幀間總體向量的幅度

$u={\sqrt {u_{1}^{2}+u_{2}^{2}+u_{3}^{2}}}$

$u^{'}={\sqrt {u_{1}^{'2}+u_{2}^{'2}+u_{3}^{'2}}}$

速度的加法 - 另一種方法

在經典物理學中，速度簡單地加起來。如果一個物體在一個參考系中以速度u運動，而這個參考系本身相對於第二個參考系以速度v運動，那麼這個物體在第二個參考系中以速度u+v運動。

這與相對論不一致，因為它預測如果光速在第一個參考系中是c，那麼它在第二個參考系中將是v+c。

我們需要找到一個組合速度的替代公式。我們可以用洛倫茲變換來做到這一點。

由於因子v/c將不斷出現，我們將這個比率稱為β。

我們正在考慮三個參考系：參考系O，參考系O'相對於參考系O以速度u運動，參考系O"相對於參考系O'以速度v運動。

我們想知道參考系O"相對於參考系O的速度，即U，在經典情況下應該是u+v。

從O到O'和O'到O"的變換可以寫成矩陣方程，

${\begin{pmatrix}x'\\ct'\end{pmatrix}}$$=\gamma {\begin{pmatrix}1&-\beta \\-\beta &1\end{pmatrix}}{\begin{pmatrix}x\\ct\end{pmatrix}}\quad$

${\begin{pmatrix}x''\\ct''\end{pmatrix}}$$=\gamma '{\begin{pmatrix}1&-\beta '\\-\beta '&1\end{pmatrix}}{\begin{pmatrix}x'\\ct'\end{pmatrix}}$

其中我們定義了β和γ為

${\begin{matrix}\beta ={\frac {u}{c}}&\gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}\\\beta ^{\prime }={\frac {v}{c}}&\gamma ^{\prime }={\frac {1}{\sqrt {1-{\beta ^{\prime }}^{2}}}}\end{matrix}}$

我們可以將這些組合起來，透過矩陣相乘得到O和O"座標之間的關係，得到

${\begin{pmatrix}x''\\ct''\end{pmatrix}}=\gamma \gamma ^{\prime }{\begin{pmatrix}1+\beta \beta '&-(\beta +\beta ')\\-(\beta +\beta ')&1+\beta \beta '\end{pmatrix}}{\begin{pmatrix}x\\ct\end{pmatrix}}\quad (1)$

這應該與兩個參考系之間的洛倫茲變換相同，

${\begin{pmatrix}x''\\ct''\end{pmatrix}}=\gamma ''{\begin{pmatrix}1&-\beta ''\\-\beta ''&1\end{pmatrix}}{\begin{pmatrix}x\\ct\end{pmatrix}}\quad (2){\mbox{ where }}{\begin{matrix}\beta ''&=&{\frac {U}{c}}\\\gamma ''&=&{\frac {1}{\sqrt {1-{\beta ''}^{2}}}}\end{matrix}}$

這兩個方程組看起來很相似。我們可以從(1)中的矩陣中提取出1+ββ'因子，使其看起來更相似

${\begin{pmatrix}x''\\ct''\end{pmatrix}}=\gamma \gamma '(1+\beta \beta '){\begin{pmatrix}1&-{\frac {\beta +\beta '}{1+\beta \beta '}}\\-{\frac {\beta +\beta '}{1+\beta \beta '}}&1\end{pmatrix}}{\begin{pmatrix}x\\ct\end{pmatrix}}$

如果以下成立，這將與方程2相同

$\beta ''={\frac {\beta +\beta '}{1+\beta \beta '}}{\mbox{ (3a) and }}\gamma ''=\gamma \gamma '(1+\beta \beta '){\mbox{ (3b)}}$

由於這兩個方程*必須*給出相同的結果，我們知道這些條件必須為真。

將β寫成速度方程3a中的形式

${\frac {U}{c}}={\frac {{\frac {u}{c}}+{\frac {v}{c}}}{1+{\frac {uv}{c^{2}}}}}$

這告訴我們*U* 與*u* 和*v* 的關係。

一點代數運算表明，這意味著方程3b 也成立。

乘以*c*，我們最終可以寫成：

$U={\frac {u+v}{1+{\frac {uv}{c^{2}}}}}$

注意，如果*u* 或*v*遠小於*c*，則分母近似為1，速度近似相加；但如果*u* 或*v*為*c*，則*U*也是*c*，正如我們預期的。

加速度變換

本節正在開發中.

上面已經看到

${\frac {u}{c}}=\tanh {\phi }$

並且，如果${\frac {v}{c}}=\tanh \beta$ 以及${\frac {u^{'}}{c}}=\tanh \epsilon$，則速度加法定理可以表示為快度的和：

$\phi =\beta +\epsilon$

如果我們對該方程關於$t$求導來研究加速度，然後假設$v$為常數

${\frac {d\phi }{dt}}={\frac {d\epsilon }{dt}}$

所以

(1) ${\frac {d\phi }{dt}}={\frac {d\epsilon }{dt^{'}}}{\frac {dt^{'}}{dt}}$

但 ${\frac {d\phi }{dt}}\!$ 也等於

${\frac {d\phi }{dt}}={\frac {d\phi }{du}}{\frac {du}{dt}}$

但是 $\phi =\tanh ^{-1}(u/c)\!$，反雙曲正切函式的導數由下式給出：

${\frac {d\tanh ^{-1}(x)}{dx}}={\frac {1}{1-x^{2}}}$

因此：

${\frac {d\phi }{du}}={\frac {1}{c}}{\frac {1}{(1-u^{2}/c^{2})}}$

為了簡潔，我們將使用以下符號：

${\frac {1}{1-u^{2}/c^{2}}}=\gamma ^{2}(u)$

即： $\gamma (u)$ 是以相對速度 $u$ 運動的觀察者的伽馬因子。

所以

(2) ${\frac {d\phi }{dt}}={\frac {1}{c}}\gamma ^{2}(u){\frac {du}{dt}}\!$

無撇和有撇觀察者觀察到的物體的速度分別為：

$u^{2}={u_{1}}^{2}+{u_{2}}^{2}+{u_{3}}^{2}\!$

$u^{'2}={u_{1}}^{'2}+{u_{2}}^{'2}+{u_{3}}^{'2}\!$

以及

$u={\frac {dr}{dt}}\!$

$u^{'}={\frac {dr^{'}}{dt^{'}}}\!$

所以

$u^{2}dt^{2}=dr^{2}\!$

$u^{'2}dt^{'2}=dr^{'2}\!$

並使用閔可夫斯基度量

$ds^{2}=dr^{2}-cdt^{2}=dr^{'2}-cdt^{'2}\!$

所以

$u^{2}dt^{2}-cdt^{2}=u^{'2}dt^{'2}-cdt^{'2}\!$

因此

$dt^{2}(c^{2}-u^{2})=dt^{'2}(u^{'2}-c^{2})\!$

給定$\gamma (u)={\frac {c}{\sqrt {c^{2}-u^{2}}}}\!$ 和 $\gamma (u^{'})={\frac {c}{\sqrt {c^{2}-u^{'2}}}}\!$

(3)${\frac {dt^{'}}{dt}}={\frac {\gamma (u^{'})}{\gamma (u)}}$

因此，將(2)和(3)代入(1)

${\frac {1}{c}}\gamma ^{2}(u){\frac {du}{dt}}={\frac {d\epsilon }{dt^{'}}}{\frac {\gamma (u^{'})}{\gamma (u)}}$

如前所述，應用arctanh的微分來確定${\frac {d\epsilon }{dt^{'}}}$

$\gamma ^{3}(u^{'}){\frac {du^{'}}{dt^{'}}}=\gamma ^{3}(u){\frac {du}{dt}}$

這與牛頓公式不同，其中 $du/dt=du^{'}/dt^{'}$。**固有加速度** $\alpha \!$定義為物體在其靜止系中的加速度。對於 $u^{'}=0\!$和$\alpha =du^{'}/dt^{'}\!$的觀察者來說，它是速度的瞬時變化。在這種情況下

$\alpha =\gamma ^{3}(u){\frac {du}{dt}}$

術語 ${\frac {du}{dt}}\!$稱為“座標加速度”。

另一種加速度方法

在經典力學中，我們會談論一個在x(t)處具有加速度d²x/dt²的粒子。在相對論中，我們必須將時間視為另一個座標，並使用相對於固有時間的導數，這意味著我們的加速度概念將發生變化。我們可以假設粒子以低於光速的速度運動。

由於τ隨著t單調遞增（不允許時間旅行），因此我們可以輕鬆地用τ而不是t引數化粒子的路徑。然後，相對於這兩個變數的導數僅相差一個γ因子

${\frac {d}{d\tau }}=\gamma {\frac {d}{dt}}$

這給了我們經典公式和相對論公式之間的聯絡。

假設我們有一個在路徑 (x(τ),ct(τ)) 上運動的粒子，其中τ是粒子的固有時間。

它的四維速度向量是

${\underline {u}}={\frac {d}{d\tau }}(x,ct)=\gamma ({\dot {\mathbf {x} }},c)$

在粒子的靜止系中，它是 (0,c)，具有恆定大小 -c²，但這個標量在所有參照系中必須相同，因此

${\underline {u}}\cdot {\underline {u}}=-c^{2}$

也就是說，速度的大小始終是恆定的。

對它求微分，我們可以立即說

${\underline {u}}\cdot {\underline {a}}={\frac {d}{d\tau }}{\underline {u}}\cdot {\underline {u}}=0$

所以，速度和加速度始終是垂直的。

這兩個結果比經典物理學中要簡單得多。

對速度求微分，經過一些代數運算後，我們得到

${\underline {a}}=\gamma ^{4}{\ddot {x}}(1,{\frac {v}{c}})$

當運動沿著x軸時。由於空間和時間分量必須分別是三維向量和標量，因此我們立即看到對於任意方向的運動，

${\underline {a}}=\gamma ^{4}\left({\ddot {\mathbf {x} }},{\frac {{\ddot {\mathbf {x} }}\cdot \mathbf {v} }{c}}\right)$

它的大小是

$|{\underline {a}}|=\gamma ^{3}{\ddot {x}}$

它是經典量值，乘以一個與 γ 有關的修正因子。當速度遠小於 c 時，此修正因子近似為 1，因此在該極限下，量值應與經典結果相同。

瞭解這一點後，我們可以計算出一個沿 x 軸以恆定加速度 a 運動的粒子的運動方程。為簡單起見，我們假設初始速度為 0。

由於加速度是恆定的

${\frac {\dot {v}}{\left(1-{\frac {v^{2}}{c^{2}}}\right)^{\frac {3}{2}}}}=a$

積分一次，我們得到

${\frac {v}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=at$

或者，重新整理後得到

$v={\frac {at}{\sqrt {1+a^{2}t^{2}/c^{2}}}}$

如果 at 遠小於 c，則速度近似為 at，與經典結果相同，但隨著 t 趨於無窮大，速度趨於 c。

位置為

$x=d+{\frac {c^{2}}{a}}{\sqrt {1+{\frac {a^{2}t^{2}}{c^{2}}}}}$

其中 d 是一個常數。我們可以選擇座標系使 d 為零。

我們用 I 表示粒子與原點之間的間隔，則有

${\begin{matrix}I^{2}&=&x^{2}&-&c^{2}t^{2}\\&=&{\frac {c^{4}}{a^{2}}}\left(1+{\frac {a^{2}t^{2}}{c^{2}}}\right)&-&c^{2}t^{2}\\&=&{\frac {c^{4}}{a^{2}}}&&\end{matrix}}$

因此粒子與原點之間的間隔是恆定的。注意，這是一個雙曲線方程，所以我們知道粒子的軌跡。

動量

經典地，動量是速度乘以質量。我們可以在相對論中使用相同的定義，看看它會帶我們到哪裡。

${\underline {p}}=m_{0}{\underline {u}}=m_{0}\gamma (\mathbf {v} ,c)$

你可能會看到這裡出現的乘積 m₀γ 被稱為 相對論質量，但我們不會使用這種方法。

質量 m₀ 通常被稱為 靜止質量，以區別於相對論質量。

四動量的空間分量顯然是經典動量，乘以一個 γ 因子。在遠小於 c 的速度下，這將近似為 1。

時間分量是 m₀γc。為了瞭解這意味著什麼，我們可以看一下 v/c 很小時的值。

$m_{0}\gamma c={\frac {m_{0}c}{\sqrt {1-v^{2}/c^{2}}}}=m_{0}c\left(1+{\frac {1}{2}}{\frac {v^{2}}{c^{2}}}+{\frac {3}{8}}{\frac {v^{4}}{c^{4}}}+\cdots \right)$

此展開式中的第一項是一個常數。

第二項是

${\frac {m_{0}v^{2}}{2c}}$

這與我們所熟知的經典動能除以光速c的結果相同。

現在，在動能的定義中新增一個常數不會產生實際的影響，因為真正重要的是能量的變化，所以我們可以將相對論動量的這個時間分量識別為能量除以c。

${\underline {p}}=(\gamma \mathbf {p} ,E/c)$

然後我們有

$E=m_{0}c^{2}+{\frac {1}{2}}m_{0}v^{2}+{\frac {3}{8}}{\frac {m_{0}v^{4}}{c^{2}}}+\cdots$

即使靜止，粒子也具有動能，

$E=m_{0}c^{2},\,$

這是最著名的相對論方程。

力

在經典力學中，我們有

$\mathbf {F} ={\frac {d\mathbf {p} }{dt}}$

我們可以簡單地透過用四維向量替換三維向量，用τ替換t，得到等效的相對論方程：

${\underline {F}}={\frac {d{\underline {p}}}{d\tau }}$

如果靜止質量是恆定的，對於所有簡單的系統都是這樣，我們可以將其改寫為

${\underline {F}}=m{\underline {a}}$

我們已經知道a，所以我們現在可以寫成

${\underline {F}}=\gamma ^{4}\left(\mathbf {F} ,{\frac {\mathbf {F} \cdot \mathbf {v} }{c}}\right)$

這個時間分量本質上是功率，即能量隨時間的變化率，這正如我們預期的那樣，因為能量是動量的時間分量。

加速參考系和事件視界

圖：時空圖顯示一個以恆定加速度運動的參考系的原點的世界線。

我們知道這條世界線是一條雙曲線，其漸近線為x=±ct。從圖中我們可以看出另一個性質。

任何來自“暮色地帶”的（x小於ct）光都無法到達加速的觀察者。因此，暮色地帶中的任何事件都不會影響觀察者。

反之，存在一個區域，其中x小於-ct，加速觀察者發出的任何光都無法到達該區域。因此，觀察者無法影響該區域中的任何事件。

由於這種特性，我們將這兩條漸近線稱為事件視界。在某種程度上，它們就像時空中的單向屏障。加速觀察者可以看見物體消失在事件視界後面，但他們永遠看不到任何物體從事件視界中重新出現。

這些特定的事件視界是與觀察者相關的，正如狹義相對論中所有事件視界一樣。然而，廣義相對論允許存在與觀察者無關的事件視界。

我們不會證明這一點，但我們可以透過使用廣義相對論的基本原理（愛因斯坦稱之為等效原理）來了解事件視界如何在廣義相對論中起作用：即引力只不過是一種慣性力。

這意味著引力在區域性與由於加速度產生的力無法區分；如果電梯門關上了，我們就無法分辨我們是處於1g的引力場中靜止，還是在零重力下以1g的加速度運動。

這表明我們可以透過研究加速參考系的特性來了解廣義相對論。

現在，由於地球上的引力指向下方，因此我們站在地球表面時必須不斷向上加速。這種對引力的解釋的明顯問題是我們似乎並沒有遠離地球中心，而這似乎是這種加速的自然結果。

然而，上一章的計算表明，即使與上述圖中彎曲世界線相關的物體正在加速遠離原點，它與原點的距離（在其自身框架中）始終保持不變。換句話說，即使我們正在加速遠離地球中心，到地球中心的距離仍然是恆定的！

因此，由於等效原理，我們可以預期看到與狹義相對論中加速觀察者相同的事物，包括一個事件視界。

在狹義相對論中的加速度情況下，慣性物體在無限時間內以c的速度穿過事件視界，相對於觀察者而言。

類似地，在廣義相對論中，自由落體物體在無限時間內以c的速度穿過事件視界，相對於靜止的觀察者而言。透過反轉軌跡，我們可以得出結論，在事件視界處，逃逸速度為c，即引力非常強，光都無法逃逸。

因此，利用等效原理和狹義相對論中的加速度行為，我們預測了黑洞。

地球內部實際上不存在事件視界，因為地球的質量不是集中在一個點上，而地球只有在地球表面之外才能被視為一個點質量，而事件視界本來應該位於地球表面之內。

紅移

解釋引力紅移的時空圖。

在引力場中，從較低水平發射的光在傳播到較高水平時，其頻率會降低。這種現象被稱為引力紅移。

我們可以利用等效原理來理解為什麼會發生這種情況。處於引力場中相當於處於加速參考系中，因此瞭解多普勒頻移在這種參考系中的工作方式將告訴我們它在引力場中的工作方式。

我們從非加速或慣性參考系觀察光的發射和吸收過程，如圖所示。在這個參考系中，光的觀察者向右加速，如圖中彎曲的紅色世界線所示，這相當於向左的引力。

光在點 A 以頻率 $\omega$ 由一個此時靜止的源發射。此時觀察者在這個參考系中也是靜止的。然而，當光到達觀察者時，他們已經有了向右的速度，這意味著觀察者測量的光的多普勒頻移頻率為 $\omega '$。由於觀察者正在遠離光源，$\omega '<\omega$，如上所示。

相對論多普勒頻移由下式給出

${\frac {\omega '}{\omega }}={\sqrt {\frac {1-U/c}{1+U/c}}},$

因此我們需要計算U/c。觀察者在點 B 的同時性線穿過原點，因此由線段 OB 給出。這條線的斜率為U/c，其中U 是觀察者在點 B 的速度。從圖中我們可以看到，這個斜率也可以用X' /X 的比率給出。

將這些等式相等，消去X，轉而用L = √(X² - X′²) 表示，這是觀察者到原點的實際不變距離，並將此結果代入上式，得到我們的引力紅移公式

${\begin{matrix}{\frac {\omega '}{\omega }}&=&{\sqrt {\frac {X-X'}{X+X'}}}&=&{\sqrt {\frac {(L^{2}+X'^{2})^{1/2}-X'}{(L^{2}+X'^{2})^{1/2}+X'}}}\\&=&{\frac {(L^{2}+X'^{2})^{1/2}-X'}{L}}&=&{\frac {X-X'}{L}}\end{matrix}}$

如果X′ = 0，則不存在紅移，因為光源與觀察者共處。另一方面，如果光源位於原點，則X′=X，多普勒頻移頻率為零。此外，光永遠不會到達觀察者，因為世界線與穿過原點的光的世界線漸近。如果光源位於比觀察者高的引力場水平，則X′ < 0，那麼頻率將轉移到更高的值，即變為藍移。

要了解這種多普勒頻移與重力g 和光源與觀察者之間距離h 的關係，首先要注意

$L={\frac {c^{2}}{g}}\qquad X-X'=L-h$

進行這些替換得到

${\frac {\omega '}{\omega }}=1-{\frac {gh}{c^{2}}}\qquad (1)$

因此紅移與重力成正比。

由於這種多普勒頻移不依賴於波的型別，我們可以得出結論，它實際上是由時間膨脹引起的，就像由於相對運動引起的多普勒頻移一樣。

也就是說，重力減慢了時間。

能量和頻率

在公式 1 中，gh 是引力勢能的變化，因此頻率的變化與勢能的變化成正比，這表明可能存在與能量守恆的聯絡。

然而，由於我們還沒有建立頻率和能量之間的任何聯絡，我們不能簡單地應用能量守恆論證。相反，我們可以反向論證，找出如果能量守恆，能量-頻率關係必須是什麼。

假設我們有兩個相同的系統，它們都靜止在均勻引力場g 中，初始能量為E，垂直距離為h。

該系統具有E/c² 的質量，賦予其勢能，因此兩個系統的總能量最初為

$E_{i}=2E-{\frac {gh}{c^{2}}}E$

其中第二項是由於下部系統勢能較低。

下部系統發射出一束頻率為 ω 的波，能量為 E(ω)。當這束波到達上部系統時，頻率已紅移為 ω'，能量為 E(ω')。該能量被上部系統吸收。

現在總能量為

$E_{f}=E-E(\omega )+E+E(\omega ')-\left(E-E(\omega )\right){\frac {gh}{c^{2}}}$

為了保持能量守恆，這兩個方程必須給出相同的結果。將它們等同起來，我們得到

$E(\omega ')=E(\omega )(1-{\frac {gh}{c^{2}}})$

將此與多普勒頻移進行比較，我們發現

${\frac {E(\omega ')}{E(\omega )}}={\frac {\omega '}{\omega }}$

這隻有在 E(ω) 與 ω 成正比時才成立

也就是說，能量守恆意味著 能量與頻率成正比，這是量子理論的一個公理。

我們也可以從量子結果出發，證明引力紅移必須存在。任何一個理論都需要另一個理論來保持一致性。

由於能量和頻率都是四維向量的時間分量，它們成正比意味著四維向量本身及其空間分量也成正比。因此，對於波來說，動量與 k 成正比。

我們還記得，之前在分析哈密頓方程時，我們看到經典力學在幾何光學極限下將等價於各向異性波的理論，如果能量與頻率成正比，動量與波數成正比。這種正比關係不僅是能量守恆所必需的，而且可以使統一波粒二象性的理論成為可能。

這些都不能真正證明這種正比關係，需要實驗才能證明，但它確實使這種假設成為一種自然假設，而實驗也確實證實了這一點。

由於以上原因，從現在開始，我們將假設能量和頻率以這種方式相關，比例常數為 $\hbar$

$(c\mathbf {p} ,E)=\hbar (c\mathbf {k} ,\omega )$

引力和曲率

引力紅移也意味著空間是彎曲的。我們可以透過考慮時空中的矩形來觀察這一點。

在沒有引力的情況下，如果我們從某個點 A 開始，等待時間 t，然後以光速向右移動距離 h，我們將到達與我們以光速移動距離 h 然後相對於 A 停留時間 t 相同的位置 B。

在引力作用下，如果我們沿著第一條路徑走，我們將上升距離 ct，然後等待時間 t。在第二條路徑上，我們首先等待時間 t，但這會因引力而膨脹。對於 B 處的觀察者來說，我們似乎等待了 t(1+gh/c²) 的時間才開始移動，因此我們最終比沿著第一條路徑走的時間晚到達 B。

因此，在引力作用下，我們以何種順序新增距離向量是有區別的。如果空間是平坦的，這種情況不可能發生，因此空間必須是彎曲的。

為了描述空間的彎曲方式，我們需要使用廣義相對論的技術。

外部連結

• 龐德-雷布卡-斯奈德實驗

勢動量

在經典物理學中，我們知道運動學通常可以用勢能來描述。現在我們已經看到，在相對論中，能量只是動量四維向量的時間分量，因此我們應該期望勢能也是如此。為了瞭解這一點，我們將從經典情況類比推理。

對於一個自由的、非相對論性的質量為 m 的粒子，總能量 E 等於動能 K，並且與粒子的動量 Π 有如下關係

$E=K={\frac {|{\boldsymbol {\Pi }}|^{2}}{2m}}\qquad {\mbox{(free, non-relativistic)}}.$

在非相對論情況下，動量為 Π= mv，其中 v 是粒子速度。

如果粒子不是自由的，而是受到與勢能 U(x,y,z) 相關的力的作用，那麼必須修改該方程，以考慮 U 對總能量的貢獻

$E-U=K={\frac {|{\boldsymbol {\Pi }}|^{2}}{2m}}\qquad {\mbox{(non-free, non-relativistic)}}.$

作用在粒子上的力與勢能的關係為

$\mathbf {F} =-\left({\frac {\partial U}{\partial x}},{\frac {\partial U}{\partial y}},{\frac {\partial U}{\partial z}}\right).$

對於自由相對論粒子，我們有

$E=(|{\boldsymbol {\Pi }}|^{2}c^{2}+m^{2}c^{4})^{1/2}\qquad {\mbox{(free, relativistic)}}.$

將力新增到相對論情況下的明顯方法是透過用勢能改寫此方程

$E-U=(|{\boldsymbol {\Pi }}|^{2}c^{2}+m^{2}c^{4})^{1/2}\qquad {\mbox{(incomplete!)}}.$

然而 ${\boldsymbol {\Pi }}=(\Pi ,E/c)$ 是一個四維向量，因此從該四維向量的單個分量中減去某個東西的方程不是相對論不變的。換句話說，該方程不遵守相對論原理，因此不能正確！

我們如何解決這個問題？一種方法是定義一個新的四維向量，其中U/c是其類時部分，而某個新的向量Q是其類空部分

${\underline {Q}}\equiv (\mathbf {Q} ,U/c)\qquad {\mbox{(potential four-momentum)}}.$

然後我們從動量Π中減去Q。當我們這樣做時，方程 (13.5) 變為

$E-U=(|{\boldsymbol {\Pi }}-\mathbf {Q} |^{2}c^{2}+m^{2}c^{4})^{1/2}\qquad {\mbox{(non-free, relativistic)}}.$

量Q稱為勢動量，Q為勢四動量。

如果 |Π-Q|遠小於mc，則它近似為

$E=mc^{2}+{\frac {1}{2m}}\left({\boldsymbol {\Pi }}-\mathbf {Q} \right)^{2}$

這種能量表達式與我們為經典速度相關力所考察的哈密頓量具有相同的形式，因此我們知道它預測了當條件滿足時，力垂直於速度。事實證明，即使條件滿足，它也是垂直的。

在經典物理學中，勢動量是一個可選的額外部分。在相對論中，它是任何勢場中不可或缺的一部分。

一些額外的術語很有用。我們定義

$\mathbf {p} \equiv {\boldsymbol {\Pi }}-\mathbf {Q} \qquad {\mbox{(kinetic momentum}})$

因為在經典情況下它簡化為mv，所以我們將它稱為動量。為了避免混淆，我們將Π 重新命名為總動量。因此，總動量等於動量加上勢動量，類似於能量。

4 動量守恆

我們之前介紹了能量和動量守恆的概念。換句話說，如果我們有一組與宇宙其他部分隔離的粒子，每個粒子都有動量 p_i 和能量 E_i，那麼粒子可以被建立和銷燬，它們可以相互碰撞。

在這些相互作用中，每個粒子的能量和動量可能會發生變化，但所有能量的總和以及所有動量的總和隨時間保持不變。

$E=\sum _{i}E_{i}={\mbox{const}}\qquad \mathbf {p} =\sum _{i}\mathbf {p} _{i}={\mbox{const}}$

用四動量表達更簡單

${\underline {p}}=\sum _{i}{\underline {p}}_{i}={\mbox{const}}$

在這一點上，像上面的這樣的陳述應該引起警鐘。在相對論的背景下，說總能量和動量隨時間保持不變究竟意味著什麼？哪個時間？哪個參考系的時間？

假設兩個粒子在左圖中粗水平線所示的時間內遠端交換四動量。四動量守恆意味著

${\underline {p}}_{A}+{\underline {p}}_{B}={\underline {p}}'_{A}+{\underline {p}}'_{B}$

其中下標字母對應於圖中的粒子標籤。帶撇號的值表示交換後的動量，而沒有撇號表示交換前的值。

現在從右圖中的參考系觀察交換。在細水平線之間的區域存在四動量守恆問題。在這個區域，粒子 B 已經轉移了它的四動量，但它還沒有被粒子 A 接收到。換句話說，在這個參考系中，四動量不守恆！

這個問題非常嚴重，我們必須從物理學庫中消除超距作用的概念。為了使粒子能夠遠端相互作用並且在所有參考系中仍然保持四動量守恆，唯一的方法是假設所有遠端相互作用都是由另一個粒子或場介導的。

如果力是由一個粒子介導的，那麼首先，粒子 A 以守恆四動量的方式發射粒子 C。其次，粒子 C 以同樣守恆的相互作用被粒子 B 吸收。

如果力是由場介導的，那麼首先，粒子 A 以守恆四動量的方式發射波 C，其動量與其波數成正比。然後，波 C 以c 或更小的速度傳播，直到它以同樣守恆的相互作用被粒子 B 吸收。

我們將看到，在量子理論中，粒子與場的區別消失了，因此這兩種圖實際上都描述了相同機制的不同視角。無論我們使用哪張圖，四動量都在所有時間和所有參考系中都守恆。

換句話說，動量和能量從粒子 A 傳遞到粒子 B 是一個兩步過程。動量在粒子或場之間傳播。