統計分析：使用 R 的入門 / 第 2 章

資料是統計分析的命脈。本書中一個反覆出現的主題是，大多數分析都包括構建合理的統計模型來解釋觀察到的資料。這需要對資料及其來源有清晰的理解。因此，瞭解可能遇到的不同型別的資料非常重要。因此，本章重點介紹不同型別的資料，包括檢查它們的一些簡單方法，以及如何將資料組織成連貫的資料集。

第 2 章中的 R 主題

本章中使用的 R 示例旨在向您介紹 R 的基礎知識，因此與本書的其他部分相比可能顯得枯燥乏味，甚至過於技術性。但是，這裡介紹的主題對於理解如何使用 R 來說是必不可少的，尤其重要的是要理解它們。它們假設您對賦值（即儲存物件）和函式的概念感到舒適，如之前所述。

變數

最簡單的型別的資料只是一組測量值，每個測量值都是一個“資料點”。在統計學中，一組相同型別單個測量值通常稱為變數，並且通常會給它們一個名稱。變數通常與之相關聯大量背景資訊：測量值代表什麼，為什麼要收集以及如何收集，是否存在任何已知的遺漏或異常點，等等。瞭解或找出此關聯資訊是任何分析的重要組成部分，以及對變數的檢查（例如，透過繪圖或其他方法）。

R 中的單個變數

v·d·e

向量

R 中最基本的物件之一是向量，用於儲存相同型別（例如資料變數）的多個測量值。向量可以儲存幾種不同型別的資料。最常見的是數值向量，其中向量的每個元素只是一個數字。其他常用的向量型別是字元向量（其中每個元素都是一段文字）和邏輯向量（其中每個元素都是TRUE或FALSE）。在本主題中，我們將使用“資料集”包提供的幾個示例向量，其中包含有關美國各州的資料（參見?state）。R 本質上是一個基於向量的程式；事實上，我們在之前的計算中使用的數字只是被視為具有單個元素的向量。這意味著 R 中的大多數基本函式在被賦予向量作為引數時將表現良好，如下所示。

輸入

state.area                #a NUMERIC vector giving the area of US states, in square miles
state.name                #a CHARACTER vector (note the quote marks) of state names 
sq.km <- state.area*2.59  #Arithmetic works on numeric vectors, e.g. convert sq miles to sq km
sq.km                     #... the new vector has the calculation applied to each element in turn
sqrt(sq.km)               #Many mathematical functions also apply to each element in turn 
range(state.area)         #But some functions return different length vectors (here, just the max & min).
length(state.area)        #and some, like this useful one, just return a single value.

結果

> state.area #一個 NUMERIC 向量，以平方英里為單位給出美國各州的面積

[1]  51609 589757 113909  53104 158693 104247   5009   2057  58560  58876   6450  83557  56400

[14] 36291 56290 82264 40395 48523 33215 10577 8257 58216 84068 47716 69686 147138 [27] 77227 110540 9304 7836 121666 49576 52586 70665 41222 69919 96981 45333 1214 [40] 31055 77047 42244 267339 84916 9609 40815 68192 24181 56154 97914 > state.name #一個 CHARACTER 向量（注意引號）的州名稱

[1] "Alabama"            "Alaska"             "Arizona"            "Arkansas"          
[5] "California"         "Colorado"           "Connecticut"        "Delaware"          
[9] "Florida"            "Georgia"            "Hawaii"             "Idaho"             

[13] "Illinois" "Indiana" "Iowa" "Kansas" [17] "Kentucky" "Louisiana" "Maine" "Maryland" [21] "Massachusetts" "Michigan" "Minnesota" "Mississippi" [25] "Missouri" "Montana" "Nebraska" "Nevada" [29] "New Hampshire" "New Jersey" "New Mexico" "New York" [33] "North Carolina" "North Dakota" "Ohio" "Oklahoma" [37] "Oregon" "Pennsylvania" "The smallest state" "South Carolina" [41] "South Dakota" "Tennessee" "Texas" "Utah" [45] "Vermont" "Virginia" "Washington" "West Virginia" [49] "Wisconsin" "Wyoming" > sq.km <- state.area*2.59 #標準算術運算適用於數值向量，例如將平方英里轉換為平方公里 > sq.km #... 給出另一個向量，其中對每個元素依次執行計算

[1]  133667.31 1527470.63  295024.31  137539.36  411014.87  269999.73   12973.31    5327.63
[9]  151670.40  152488.84   16705.50  216412.63  146076.00   93993.69  145791.10  213063.76

[17] 104623.05 125674.57 86026.85 27394.43 21385.63 150779.44 217736.12 123584.44 [25] 180486.74 381087.42 200017.93 286298.60 24097.36 20295.24 315114.94 128401.84 [33] 136197.74 183022.35 106764.98 181090.21 251180.79 117412.47 3144.26 80432.45 [41] 199551.73 109411.96 692408.01 219932.44 24887.31 105710.85 176617.28 62628.79 [49] 145438.86 253597.26 > sqrt(sq.km) #許多數學函式也依次應用於每個元素

[1]  365.60540 1235.90883  543.16140  370.86299  641.10441  519.61498  113.90044   72.99062
[9]  389.44884  390.49819  129.24976  465.20171  382.19890  306.58390  381.82601  461.58830

[17] 323.45487 354.50609 293.30334 165.51263 146.23826 388.30328 466.62203 351.54579 [25] 424.83731 617.32278 447.23364 535.06878 155.23324 142.46136 561.35100 358.33202 [33] 369.04978 427.81111 326.74911 425.54695 501.17940 342.65503 56.07370 283.60615 [41] 446.71213 330.77479 832.11058 468.96955 157.75712 325.13205 420.25859 250.25745 [49] 381.36447 503.58441 > range(state.area) #但是有些函式返回不同長度的向量（此處，僅返回最大值和最小值）。 [1] 1214 589757 > length(state.area) #並且有些函式，像這個有用的函式一樣，只返回一個值。 [1] 50

注意，您輸出的第一部分可能與上面的略有不同。根據螢幕的寬度，每行輸出的元素數量可能不同。這就是方括號中的數字產生的原因，它們是在向量列印到螢幕上時產生的。這些帶括號的數字給出該行上第一個元素的位置，這是一種有用的視覺輔助。例如，檢視 state.name 的列印輸出，並從第二行開始計數，我們可以知道第八個州是特拉華州。

您可能偶爾需要從頭開始建立自己的向量（儘管大多數向量都是從處理現有檔案中的資料獲得的）。構造向量最常用的函式是c()，之所以這樣命名是因為它concatenates 物件。但是，如果您希望建立由數字的規則序列組成的向量（例如 2,4,6,8,10,12 或 1,1,2,2,1,1,2,2），則可以使用幾個備用函式，包括seq()、rep() 和: 運算子。

輸入

c("one", "two", "three", "pi")  #Make a character vector
c(1,2,3,pi)                     #Make a numeric vector
seq(1,3)                        #Create a sequence of numbers
1:3                             #A shortcut for the same thing (but less flexible)
i <- 1:3                        #You can store a vector
i
i <- c(i,pi)                    #To add more elements, you must assign again, e.g. using c() 
i                             
i <- c(i, "text")               #A vector cannot contain different data types, so ... 
i                               #... R converts all elements to the same type
i+1                             #The numbers are now strings of text: arithmetic is impossible 
rep(1, 10)                      #The "rep" function repeats its first argument
rep(3:1,10)                     #The first argument can also be a vector
huge.vector <- 0:(10^7)         #R can easily cope with very big vectors
#huge.vector #VERY BAD IDEA TO UNCOMMENT THIS, unless you want to print out 10 million numbers
rm(huge.vector)                 #"rm" removes objects. Deleting huge unused objects is sensible

結果

> c("one", "two", "three", "pi") #製作一個字元向量

[1] "one" "two" "three" "pi" > c(1,2,3,pi) #製作一個數值向量 [1] 1.000000 2.000000 3.000000 3.141593 > seq(1,3) #建立一系列數字 [1] 1 2 3 > 1:3 #相同操作的快捷方式（但靈活性較差） [1] 1 2 3 > i <- 1:3 #您可以儲存一個向量 > i [1] 1 2 3 > i <- c(i,pi) #要新增更多元素，您必須重新賦值，例如使用 c() > i [1] 1.000000 2.000000 3.000000 3.141593 > i <- c(i, "text") #向量不能包含不同的資料型別，因此... > i #... R 將所有元素轉換為相同型別 [1] "1" "2" "3" "3.14159265358979" "text" > i+1 #現在數字是文字字串：算術運算是不可能的 錯誤：非數值引數傳給二元運算子 > rep(1, 10) #“rep”函式重複其第一個引數

[1] 1 1 1 1 1 1 1 1 1 1

> rep(3:1,10) #第一個引數也可以是一個向量

[1] 3 2 1 3 2 1 3 2 1 3 2 1 3 2 1 3 2 1 3 2 1 3 2 1 3 2 1 3 2 1

> huge.vector <- 0:(10^7) #R 可以輕鬆應對非常大的向量 > #huge.vector #除非您想打印出 1000 萬個數字，否則請不要取消註釋此行 > rm(huge.vector) #"rm" 刪除物件。刪除巨大的未使用的物件是明智的

v·d·e

訪問向量元素

我們經常希望訪問向量中的某些元素：例如，我們可能只想使用第 10 個元素，或者前 4 個元素，或者根據元素的值選擇元素。實現這一點的方法是獲取向量並在其前面新增索引運算子 []（即方括號）。如果這些方括號包含

• 一個或多個正數，那麼它的效果是選取向量的那些特定元素
• 一個或多個負數，那麼它的效果是選取整個向量，除了那些元素
• 一個邏輯向量，那麼邏輯向量中的每個元素都指示是否選取（如果為 TRUE）或不選取（如果為 FALSE）原始向量中的等效元素。

邏輯向量的使用可能看起來有點複雜。但是，它們非常有用，因為它們是使用比較運算子的關鍵。例如，可以使用它們來識別哪些美國州面積較小，面積小於（<）10 000 平方英里（如下所示）。

輸入

min(state.area)    #This gives the area of the smallest US state...
which.min(state.area) #... this shows which element it is (the 39th as it happens) 
state.name[39]     #You can obtain individual elements by using square brackets
state.name[39] <- "THE SMALLEST STATE" #You can replace elements using [] too
state.name       #The 39th name ("Rhode Island") should now have been changed
state.name[1:10]    #This returns a new vector consisting of only the first 10 states
state.name[-(1:10)]  #Using negative numbers gives everything but the first 10 states
state.name[c(1,2,2,1)] #You can also obtain the same element multiple times
###Logical vectors are a little more complicated to get your head round
state.area < 10000       #A LOGICAL vector, identifying which states are small
state.name[state.area < 10000] #So this can be used to select the names of the small states

結果

> min(state.area) # 這將給出美國最小州的面積...

[1] 1214 > which.min(state.area) # ... 這將顯示它是哪個元素（恰好是第 39 個） [1] 39 > state.name[39] # 你可以使用方括號獲取單個元素 [1] "Rhode Island" > state.name[39] <- "The smallest state" # 你也可以使用 [] 替換元素 > state.name # 第 39 個名稱（"Rhode Island"）現在應該已更改

[1] "Alabama"      "Alaska"       "Arizona"      "Arkansas"     
[5] "California"     "Colorado"      "Connecticut"    "Delaware"     
[9] "Florida"      "Georgia"      "Hawaii"       "Idaho"       

[13] "Illinois" "Indiana" "Iowa" "Kansas" [17] "Kentucky" "Louisiana" "Maine" "Maryland" [21] "Massachusetts" "Michigan" "Minnesota" "Mississippi" [25] "Missouri" "Montana" "Nebraska" "Nevada" [29] "New Hampshire" "New Jersey" "New Mexico" "New York" [33] "North Carolina" "North Dakota" "Ohio" "Oklahoma" [37] "Oregon" "Pennsylvania" "THE SMALLEST STATE" "South Carolina" [41] "South Dakota" "Tennessee" "Texas" "Utah" [45] "Vermont" "Virginia" "Washington" "West Virginia" [49] "Wisconsin" "Wyoming" > state.name[1:10] # 這將返回一個新向量，該向量僅包含前 10 個州

[1] "Alabama"   "Alaska"   "Arizona"   "Arkansas"  "California" "Colorado"  
[7] "Connecticut" "Delaware"  "Florida"   "Georgia"  

> state.name[-(1:10)] # 使用負數將給出除了前 10 個州之外的所有州

[1] "Hawaii"       "Idaho"       "Illinois"      "Indiana"      
[5] "Iowa"        "Kansas"       "Kentucky"      "Louisiana"     
[9] "Maine"       "Maryland"      "Massachusetts"   "Michigan"     

[13] "Minnesota" "Mississippi" "Missouri" "Montana" [17] "Nebraska" "Nevada" "New Hampshire" "New Jersey" [21] "New Mexico" "New York" "North Carolina" "North Dakota" [25] "Ohio" "Oklahoma" "Oregon" "Pennsylvania" [29] "THE SMALLEST STATE" "South Carolina" "South Dakota" "Tennessee" [33] "Texas" "Utah" "Vermont" "Virginia" [37] "Washington" "West Virginia" "Wisconsin" "Wyoming" > state.name[c(1,2,2,1)] # 你也可以多次獲取相同的元素 [1] "Alabama" "Alaska" "Alaska" "Alabama" > ### 邏輯向量有點難理解 > state.area < 10000 # 一個邏輯向量，識別哪些州面積較小

[1] FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE FALSE FALSE TRUE FALSE FALSE FALSE FALSE

[16] FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE [31] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE TRUE [46] FALSE FALSE FALSE FALSE FALSE > state.name[state.area < 10000] # 因此，這可以用來選擇小州的名稱 [1] "Connecticut" "Delaware" "Hawaii" "Massachusetts" [5] "New Hampshire" "New Jersey" "THE SMALLEST STATE" "Vermont"

雖然 [] 運算子可以用來訪問向量的單個元素，但它對於一次訪問多個元素特別有用。另一個運算子，雙方括號 ([[) 用於專門訪問單個元素。雖然對於向量來說不是特別有用，但它對於 # 列表 和 # 資料框 來說非常有用。

v·d·e

邏輯運算

當 訪問向量中的元素 時，我們看到了如何使用涉及小於號（<）的簡單邏輯表示式來生成邏輯向量，然後可以使用該向量來選擇小於某個值的元素。這種型別的邏輯運算非常有用。除了 < 之外，還有一些其他比較運算子。以下是完整集合（有關更多詳細資訊，請參見 ?Comparison）

• <（小於）和 <=（小於或等於）
• >（大於）和 >=（大於或等於）
• ==（等於）和 !=（不等於）

透過使用and、or 和not組合邏輯向量，可以獲得更大的靈活性。例如，我們可能想要識別哪些美國州的面積小於 10 000 或大於 100 000 平方英里，或者識別哪些州的面積大於 100 000 平方英里並且名稱很短。下面的程式碼展示瞭如何使用以下 R 符號來實現這一點

• & ("and")
• | ("or")
• ! ("not")

在使用邏輯向量時，以下函式特別有用，如下所示

• which() 識別邏輯向量中哪些元素為 TRUE
• sum() 可用於給出邏輯向量中為 TRUE 的元素數量。這是因為 sum() 強制將其輸入轉換為數字，如果 TRUE 和 FALSE 轉換為數字，它們將分別取值 1 和 0。
• ifelse() 根據邏輯向量中每個元素是 TRUE 還是 FALSE 返回不同的值。具體來說，諸如 ifelse(aLogicalVector, vectorT, vectorF) 之類的命令將採用 aLogicalVector 並返回，對於每個為 TRUE 的元素，返回 vectorT 中的對應元素，對於每個為 FALSE 的元素，返回 vectorF 中的對應元素。額外的說明是，如果 vectorT 或 vectorF 比 aLogicalVector 短，它們將透過複製擴充套件到正確的長度。

輸入

### In these examples, we'll reuse the American states data, especially the state names
### To remind yourself of them, you might want to look at the vector "state.names"

nchar(state.name)       # nchar() returns the number of characters in strings of text ...
nchar(state.name) <= 6  #so this indicates which states have names of 6 letters or fewer
ShortName <- nchar(state.name) <= 6         #store this logical vector for future use
sum(ShortName)          #With a logical vector, sum() tells us how many are TRUE (11 here)
which(ShortName)        #These are the positions of the 11 elements which have short names
state.name[ShortName]   #Use the index operator [] on the original vector to get the names
state.abb[ShortName]    #Or even on other vectors (e.g. the 2 letter state abbreviations)

isSmall <- state.area < 10000  #Store a logical vector indicating states <10000 sq. miles
isHuge  <- state.area > 100000 #And another for states >100000 square miles in area
sum(isSmall)                   #there are 8 "small" states
sum(isHuge)                    #coincidentally, there are also 8 "huge" states

state.name[isSmall | isHuge]   # | means OR. So these are states which are small OR huge
state.name[isHuge & ShortName] # & means AND. So these are huge AND with a short name
state.name[isHuge & !ShortName]# ! means NOT. So these are huge and with a longer name

### Examples of ifelse() ###

ifelse(ShortName, state.name, state.abb) #mix short names with abbreviations for long ones
# (think of this as "*if* ShortName is TRUE then use state.name *else* use state.abb)

### Many functions in R increase input vectors to the correct size by duplication ###
ifelse(ShortName, state.name, "tooBIG")   #A silly example: the 3rd argument is duplicated
size <- ifelse(isSmall, "small", "large") #A more useful example, for both 2nd & 3rd args
size                                      #might be useful as an indicator variable?             
ifelse(size=="large", ifelse(isHuge, "huge", "medium"), "small") #A more complex example

結果

> ### In these examples, we'll reuse the American states data, especially the state names
> ### To remind yourself of them, you might want to look at the vector "state.names"
>  
> nchar(state.name)       # nchar() returns the number of characters in strings of text ...
 [1]  7  6  7  8 10  8 11  8  7  7  6  5  8  7  4  6  8  9  5  8 13  8  9 11  8  7  8  6 13
[30] 10 10  8 14 12  4  8  6 12 12 14 12  9  5  4  7  8 10 13  9  7
> nchar(state.name) <= 6  #so this indicates which states have names of 6 letters or fewer
 [1] FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE
[15]  TRUE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
[29] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
[43]  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
> ShortName <- nchar(state.name) <= 6         #store this logical vector for future use
> sum(ShortName)          #With a logical vector, sum() tells us how many are TRUE (11 here)
[1] 11
> which(ShortName)        #These are the positions of the 11 elements which have short names
 [1]  2 11 12 15 16 19 28 35 37 43 44
> state.name[ShortName]   #Use the index operator [] on the original vector to get the names
 [1] "Alaska" "Hawaii" "Idaho"  "Iowa"   "Kansas" "Maine"  "Nevada" "Ohio"   "Oregon"
[10] "Texas"  "Utah"  
> state.abb[ShortName]    #Or even on other vectors (e.g. the 2 letter state abbreviations)
 [1] "AK" "HI" "ID" "IA" "KS" "ME" "NV" "OH" "OR" "TX" "UT"
>  
> isSmall <- state.area < 10000  #Store a logical vector indicating states <10000 sq. miles
> isHuge  <- state.area > 100000 #And another for states >100000 square miles in area
> sum(isSmall)                   #there are 8 "small" states
[1] 8
> sum(isHuge)                    #coincidentally, there are also 8 "huge" states
[1] 8
>  
> state.name[isSmall | isHuge]   # | means OR. So these are states which are small OR huge
 [1] "Alaska"        "Arizona"       "California"    "Colorado"      "Connecticut"  
 [6] "Delaware"      "Hawaii"        "Massachusetts" "Montana"       "Nevada"       
[11] "New Hampshire" "New Jersey"    "New Mexico"    "Rhode Island"  "Texas"        
[16] "Vermont"      
> state.name[isHuge & ShortName] # & means AND. So these are huge AND with a short name
[1] "Alaska" "Nevada" "Texas" 
> state.name[isHuge & !ShortName]# ! means NOT. So these are huge and with a longer name
[1] "Arizona"    "California" "Colorado"   "Montana"    "New Mexico"
>  
> ### Examples of ifelse() ###
>  
> ifelse(ShortName, state.name, state.abb) #mix short names with abbreviations for long ones
 [1] "AL"     "Alaska" "AZ"     "AR"     "CA"     "CO"     "CT"     "DE"     "FL"    
[10] "GA"     "Hawaii" "Idaho"  "IL"     "IN"     "Iowa"   "Kansas" "KY"     "LA"    
[19] "Maine"  "MD"     "MA"     "MI"     "MN"     "MS"     "MO"     "MT"     "NE"    
[28] "Nevada" "NH"     "NJ"     "NM"     "NY"     "NC"     "ND"     "Ohio"   "OK"    
[37] "Oregon" "PA"     "RI"     "SC"     "SD"     "TN"     "Texas"  "Utah"   "VT"    
[46] "VA"     "WA"     "WV"     "WI"     "WY"    
> # (think of this as "*if* ShortName is TRUE then use state.name *else* use state.abb)
>  
> ### Many functions in R increase input vectors to the correct size by duplication ###
> ifelse(ShortName, state.name, "tooBIG")   #A silly example: the 3rd argument is duplicated
 [1] "tooBIG" "Alaska" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG"
[10] "tooBIG" "Hawaii" "Idaho"  "tooBIG" "tooBIG" "Iowa"   "Kansas" "tooBIG" "tooBIG"
[19] "Maine"  "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG"
[28] "Nevada" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "Ohio"   "tooBIG"
[37] "Oregon" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG" "Texas"  "Utah"   "tooBIG"
[46] "tooBIG" "tooBIG" "tooBIG" "tooBIG" "tooBIG"
> size <- ifelse(isSmall, "small", "large") #A more useful example, for both 2nd & 3rd args
> size                                      #might be useful as an indicator variable?             
 [1] "large" "large" "large" "large" "large" "large" "small" "small" "large" "large"
[11] "small" "large" "large" "large" "large" "large" "large" "large" "large" "large"
[21] "small" "large" "large" "large" "large" "large" "large" "large" "small" "small"
[31] "large" "large" "large" "large" "large" "large" "large" "large" "small" "large"
[41] "large" "large" "large" "large" "small" "large" "large" "large" "large" "large"
> ifelse(size=="large", ifelse(isHuge, "huge", "medium"), "small") #A more complex example
 [1] "medium" "huge"   "huge"   "medium" "huge"   "huge"   "small"  "small"  "medium"
[10] "medium" "small"  "medium" "medium" "medium" "medium" "medium" "medium" "medium"
[19] "medium" "medium" "small"  "medium" "medium" "medium" "medium" "huge"   "medium"
[28] "huge"   "small"  "small"  "huge"   "medium" "medium" "medium" "medium" "medium"
[37] "medium" "medium" "small"  "medium" "medium" "medium" "huge"   "medium" "small" 
[46] "medium" "medium" "medium" "medium" "medium"

如果你做過任何計算機程式設計，你可能更習慣在 "if" 語句的上下文中處理邏輯。雖然 R 也有一個 if() 語句，但在處理向量時它不太有用。例如，以下 R 表示式

if(aVariable == 0) then print("zero") else print("not zero")

期望 aVariable 是一個單一數字：如果該數字為 0，則輸出 "zero"，如果該數字不是 0，則輸出 "not zero"。如果 aVariable 是一個包含 2 個或更多值的向量，則只有第一個元素算數：所有其他元素都被忽略。也有一些邏輯運算子會忽略除了向量中的第一個元素之外的所有元素：它們是 && 用於 AND 和 || 用於 OR。

v·d·e

缺失資料

在收集資料時，某些資料點通常是未知的。這有多種原因。例如，在分析實驗資料時，我們可能會為每個實驗記錄多個變數（例如溫度、一天中的時間等），但可能忘記（或無法）在某次記錄溫度。或者在收集美國州的社會資料時，某些州可能沒有記錄我們感興趣的某些統計資料。另一個例子是泰坦尼克號沉沒的船舶乘客資料，經過仔細研究，已經確定了船上 2207 人的票務等級，但無法確定 10 多名遇難者的年齡（見 http://www.encyclopedia-titanica.org）。我們可以簡單地省略缺失資料，但在許多情況下，我們對某些變數有資訊，但對其他變數沒有資訊。例如，我們可能不希望完全從分析中省略一個美國州，僅僅因為它缺少一個特定感興趣的資料。出於這個原因，R 提供了一個特殊的值，NA，表示 "不可用"。任何向量，數字、字元或邏輯都可以具有為NA 的元素。這些可以透過函式 "is.na" 來識別。

輸入

some.missing <- c(1,NA)
is.na(some.missing)

結果

some.missing <- c(1,NA)

is.na(some.missing) [1] FALSE TRUE

請注意，如果存在缺失資料，一些分析很難進行。你可以使用 "complete.cases" 或 "na.omit" 來構建包含省略缺失值的 datasets。

測量值

任何變數的一個重要特徵是它允許具有的值。例如，諸如性別之類的變數只能取有限數量的值（在本例中為 'Male' 和 'Female'），而諸如人體高度之類的變數可以取介於約 0 和 3 米之間的任何數值。這是一種顯而易見的背景資訊，不能從資料中推斷出來，但對分析至關重要。通常只有有限數量的此類資訊直接輸入到統計分析軟體中。與往常一樣，考慮這些背景資訊非常重要。這通常可以使用這種商品來完成 - 這對於計算機來說是不可用的 - 稱為常識。例如，計算機可以用來分析人體高度，而無需意識到一個人被記錄為（例如）175 米，而不是 1.75 米。計算機可以盲目地對該變數進行分析，而不會注意到錯誤，即使對於人類來說，這是顯而易見的。這是在分析之前繪製資料的首要原因之一。

分類變數與定量變數

儘管如此，分析軟體仍然需要一些關於變數的資訊（實際上，通常必須提供這些資訊）。幾乎所有統計軟體包都要求您至少區分**分類**變數（例如*性別*），其中每個資料點取固定數量的預定義“級別”之一，以及**定量**變數（例如*人類身高*），其中每個資料點是定義良好的尺度上的數字。表 2.1 中提供了更多示例。這種區別即使對於像求平均值這樣簡單的分析也很重要：對定量變數有意義的過程，但對分類變數卻很少有意義（“男性”和“女性”的“平均”性別是什麼？）。

表 2.1 變數型別的示例。本書後面將使用其中許多變數。

**分類**（也稱為“定性”變數或“因素”）	變數*性別*，其中每個資料點是人類的性別（即級別為“男性”或“女性”）
	變數*艙位*，其中每個資料點是船上乘客的艙位（級別為“1 等”，“2 等”或“3 等”）
**定量**（也稱為“數值”變數或“協變數”）	變數*體重變化*，其中每個點是厭食症患者在固定時間段內的體重變化。 變數*土地面積*，其中每個資料點是一個正數，表示一塊土地的面積。 變數*蝦*，其中每個資料點是確定蝦雞尾酒製劑中蝦的百分比（！） 變數*每年死亡人數*，其中資料點是特定年份中因特定原因死亡的人數。 變數*病例*，其中每個資料點是特定群體中患有特定疾病的人數。除非我們還有一些關於群體規模的度量，否則這可能毫無意義。這可以透過另一個變數（通常標記為*對照*）來實現，該變數指示每個群體中沒有患病的人數（這種型別的分組病例/對照研究在醫學等領域很常見）。
	變數*華氏溫度*，其中每個資料點是每月平均溫度（以華氏度為單位）。
	變數*方向*，其中每個資料點是羅盤方向（以度為單位）。

從原始資料中並不總是立即顯而易見變數是分類變數還是定量變數：通常，必須仔細考慮資料的上下文才能做出判斷。例如，包含數字 1、2 和 3 的變數似乎是一個數值，但它也可能是一個描述（例如）使用藥物 1、藥物 2 或藥物 3 的醫療處理的分類變數。更罕見的是，看似分類變數（例如顏色（級別“藍色”、“綠色”、“黃色”、“紅色”））可能更好地表示為數值，例如實驗中發射的光的波長。同樣，根據您要執行的操作，由您做出這種判斷。

邊界分類/定量變數

儘管分類/定量區分很重要（並且在許多教科書中都很突出），但現實並不總是如此清晰。有時將分類變數視為定量變數或反之亦然是合理的。也許最常見的情況是，當分類變數的級別似乎具有自然順序時，例如表 2.1 中的*艙位*變數，或者問卷調查中經常使用的李克特量表。

在罕見且特定的情況下，並且取決於所提出的問題的性質，可能存在可以分配給每個級別的粗略數值。例如，也許一項調查問卷附帶了一個視覺量表，其中李克特類別標記在從“完全同意”到“完全不同意”的範圍內。在這種情況下，將分類變數直接轉換為定量變數可能是合理的。

更常見的是，級別的順序是已知的，但無法普遍達成一致的精確值。這種分類變數可以描述為**有序**或**排名**，而不是像*性別*或*自稱宗教*這樣純粹是**名義**的。因此，我們可以識別出兩種主要的分類變數型別：有序（“序數”）和無序（“名義”），如表 2.1 中的兩個示例所示。

定量變數的分類

儘管分類/定量劃分是最重要的劃分，但我們還可以進一步細分每種型別（正如我們在討論分類變數時已經看到的那樣）。最常教授的分類是斯蒂文斯 (1946) 提出的。除了將分類變數分為序數和名義型別之外，他還根據所用尺度的性質將定量變數分為兩種型別，即**間隔**或**比率**。可以將**迴圈**變數新增到此分類中。因此，根據測量尺度對定量變數進行分類會導致三種細分（如表 2.1 中的細分所示）。

• 比率資料是最常見的。示例包括距離、時間長度、專案數量等。這些變數是在具有自然零點的尺度上測量的；因為我們可以使用僅包含正整數的數字。
• 間隔資料是在沒有自然零點的尺度上測量的。最常見的示例是溫度（以攝氏度或華氏度為單位）和日曆日期。由於尺度上的零點本質上是任意的，因此這個名稱來自這樣一個事實，即比率沒有意義，而間隔是有意義的。例如，意味著****
• 迴圈資料是在“環繞”的尺度上測量的，例如*方向*、*時間*、*經度*等。***

斯蒂文斯分類不是對定量變數進行分類的唯一方法。另一個合理的劃分認識到了**連續**測量和**離散**測量之間的區別。具體來說，定量變數可以表示以下兩種情況：

• 連續資料，其中討論中間值是有意義的（例如 1.2 小時、12.5% 等）。這包括資料被四捨五入的情況***。
• “離散資料”，其中中間值毫無意義（例如，討論 1.2 人死亡或 10 人群體中 2.6 例癌症病例沒有太大意義）。這些通常是事物的**計數**：這有時被稱為**計量**資料。

在實踐中，離散資料通常被視為連續資料，尤其是在它們被劃分的單位相對較小時。例如，不同國家的人口規模理論上是離散的（你不能有半個人的），但這些值非常大，因此將這些資料視為連續資料可能是合理的。但是，對於較小的值，例如一個家庭的人數，資料是相當“粒度”的，並且值的離散性質變得非常明顯。這方面的一個常見結果是存在多個重複值（例如，在大多數資料集中，將會有許多 2 人家庭）。

對定量變數進行分類的第三種方法取決於尺度是否具有上限或下限，甚至兩者兼而有之。

• 在一端有界（例如*土地面積*不能低於 0），
• 在兩端有界（例如，百分比不能小於 0 或大於 100）。另見截斷資料***
• 無界（*體重減輕*）。

最重要的是迴圈——通常需要非常不同的分析工具。通常最好以某種方式使其線性（例如，與固定方向的差異）。

間隔資料不能使用比率（除法）。相當罕見

邊界：通常有下限。只有上限的情況很少見。兩者通常表示百分比。——通常透過變換來處理（例如對數）

計數資料：如果有多個相同的值，可能會影響繪圖等。如果為真正的獨立計數，則表示誤差函式。

不同型別變數之間的區別在圖***中進行了總結。請注意，通常還會

資料點的獨立性

實際值是否會導致“周圍”值的關聯（例如時間序列），或者兩者是否反映了某些共同的關聯（例如塊/異質性）。

時間序列 空間資料 塊

整合資訊

時間序列，非獨立性的其他來源

v·d·e

因素

R 中的分類變數儲存為一個稱為**因素**的特殊向量物件。這與填充了一組名稱的字元向量不同（不要將兩者混淆）。特別是，必須告訴 R 每個元素只能是若干個已知*級別*之一（例如*男性*或*女性*）。如果您嘗試將具有不同未知級別的點放入因素中，R 會報錯。當您將因素列印到螢幕上時，R 還會列出該因素可以接受的可能級別（這可能包括不存在的級別）。

factor() 函式建立因子並定義可用級別。預設情況下，級別取自向量中的級別***。實際上，您通常不需要使用 factor()，因為從檔案讀取資料時，R 預設情況下會假設文字應轉換為因子（參見 統計分析：使用 R 的入門/R/資料幀）。您可能需要使用 as.factor()。在內部，R 將級別儲存為從 1 開始的數字，但並非總是很清楚哪個數字對應哪個級別，通常不需要知道。

有序變數，即級別具有自然順序的因子，在 R 中被稱為有序因子。它們可以透過建立因子的正常方式建立，但另外指定 ordered=TRUE。

輸入

state.region #因子示例：請注意級別已打印出來

state.name #這不是因子 state.name[1] <- "Any text" #您可以在字元向量中替換文字 state.region[1] <- "Any text" #但您不能在因子中替換文字 state.region[1] <- "South" #這可以 state.abb #這不是因子，只是一個字元向量

character.vector <- c("Female", "Female", "Male", "Male", "Male", "Female", "Female", "Male", "Male", "Male", "Male", "Male", "Female", "Female" , "Male", "Female", "Female", "Male", "Male", "Male", "Male", "Female", "Female", "Female", "Female", "Male", "Male", "Male", "Female" , "Male", "Female", "Male", "Male", "Male", "Male", "Male", "Female", "Male", "Male", "Male", "Male", "Female", "Female", "Female") #a bit tedious to do all that typing

1. 使用程式碼可能更容易，例如，女性為 1，男性為 2

Coded <- factor(c(1, 1, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 1, 1, 2, 1, 1, 2, 2, 2, 2, 1, 1, 1, 1, 2, 2, 2, 1, 2, 1, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 1, 1, 1)) Gender <- factor(Coded, labels=c("Female", "Male")) #然後我們可以將其轉換為命名級別

結果

v·d·e

矩陣和陣列

許多統計理論使用 矩陣代數。雖然本書不需要深入理解矩陣，但瞭解 R 如何處理它們是有用的。

本質上，矩陣（複數：矩陣）是向量的二維等價物。換句話說，它是一個由數字組成的矩形網格，按行和列排列。在 R 中，可以透過 matrix() 函式建立矩陣物件，該函式第一個引數是用來填充矩陣的數字向量，第二個和第三個引數分別是行數和列數。

R 還可以使用陣列物件，它們類似於矩陣，但可以具有超過 2 個維度。這些對於表格特別有用：一種包含根據各種標準分類的資料計數的陣列。這些“列聯表”的示例是下面顯示的 HairEyeColor 和 Titanic 表。

與向量一樣，索引運算子 [] 可用於訪問矩陣或陣列中的單個元素或元素集。這是透過用逗號分隔括號內的數字來完成的。例如，對於矩陣，您需要指定行索引，然後是一個逗號，然後是列索引。如果行索引為空，則假定您想要所有行，列同理。

輸入

m <- matrix(1:12, 3, 4)      #Create a 3x4 matrix filled with numbers 1 to 12
m                            #Display it!
m*2                          #Arithmetic, just like with vectors
m[2,3]                       #Pick out a single element (2nd row, 3rd column)
m[1:2, 2:4]                  #Or a range (rows 1 and 2, columns 2, 3, and 4.)
m[,1]                        #If the row index is missing, assume all rows
m[1,]                        #Same for columns
m[,2] <- 99                  #You can assign values to one or more elements
m                            #See!
###Some real data, stored as "arrays"
HairEyeColor                 #A 3D array
HairEyeColor[,,1]            #Select only the males to make it a 2D matrix
Titanic                      #A 4D array
Titanic[1:3,"Male","Adult",] #A matrix of only the adult male passengers

結果

> m <- matrix(1:12, 3, 4)      #Create a 3x4 matrix filled with numbers 1 to 12
> m                            #Display it!
     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12
> m*2                          #Arithmetic, just like with vectors
     [,1] [,2] [,3] [,4]
[1,]    2    8   14   20
[2,]    4   10   16   22
[3,]    6   12   18   24
> m[2,3]                       #Pick out a single element (2nd row, 3rd column)
[1] 8
> m[1:2, 2:4]                  #Or a range (rows 1 and 2, columns 2, 3, and 4.)
     [,1] [,2] [,3]
[1,]    4    7   10
[2,]    5    8   11
> m[,1]                        #If the row index is missing, assume all rows
[1] 1 2 3
> m[1,]                        #Same for columns
[1]  1  4  7 10
> m[,2] <- 99                  #You can assign values to one or more elements
> m                            #See!
     [,1] [,2] [,3] [,4]
[1,]    1   99    7   10
[2,]    2   99    8   11
[3,]    3   99    9   12
> ###Some real data, stored as "arrays"
> HairEyeColor                 #A 3D array
, , Sex = Male

       Eye
Hair    Brown Blue Hazel Green
  Black    32   11    10     3
  Brown    53   50    25    15
  Red      10   10     7     7
  Blond     3   30     5     8

, , Sex = Female

       Eye
Hair    Brown Blue Hazel Green
  Black    36    9     5     2
  Brown    66   34    29    14
  Red      16    7     7     7
  Blond     4   64     5     8

> HairEyeColor[,,1]            #Select only the males to make it a 2D matrix
       Eye
Hair    Brown Blue Hazel Green
  Black    32   11    10     3
  Brown    53   50    25    15
  Red      10   10     7     7
  Blond     3   30     5     8
> Titanic                      #A 4D array
, , Age = Child, Survived = No

      Sex
Class  Male Female
  1st     0      0
  2nd     0      0
  3rd    35     17
  Crew    0      0

, , Age = Adult, Survived = No

      Sex
Class  Male Female
  1st   118      4
  2nd   154     13
  3rd   387     89
  Crew  670      3

, , Age = Child, Survived = Yes

      Sex
Class  Male Female
  1st     5      1
  2nd    11     13
  3rd    13     14
  Crew    0      0

, , Age = Adult, Survived = Yes

      Sex
Class  Male Female
  1st    57    140
  2nd    14     80
  3rd    75     76
  Crew  192     20

> Titanic[1:3,"Male","Adult",] #A matrix of only the adult male passengers
     Survived
Class  No Yes
  1st 118  57
  2nd 154  14
  3rd 387  75

v·d·e

列表

R 對向量中可以包含的內容非常嚴格。所有元素都需要是相同型別，而且必須是數字型別、邏輯值或文字字串。如果要建立一個包含不同型別的元素的集合，或者這些元素型別不是允許的向量型別之一，則需要使用列表。

輸入

l1 <- list(a=1, b=1:3)
l2 <- c(sqrt, log) #

結果

視覺化單個變數

在進行正式分析之前，您應該始終執行初始資料分析，其中一部分是對要分析的變數進行檢查。如果資料點很少，可以目測掃描數字，但通常透過繪製圖表來檢查資料更容易。

散點圖，例如第 1 章中的那些，可能是最熟悉的圖表型別，對於顯示兩個變數之間的關聯模式很有用。這些將在本章後面討論，但在本節中，我們首先檢查視覺化單個變數的各種方法。

單個變數的圖表，或單變數圖表，尤其用於探索變數的分佈；即其形狀和位置。除了對資料的初始檢查外，這些圖表的另一個非常常見的用途是檢視殘差（見圖 1.2）：在擬合統計模型後剩餘的未解釋資料部分。關於這些殘差分佈的假設通常透過繪製它們來檢查。

以下圖表說明了單變數圖表的幾種更常見的型別。經典文字是 Tufte（引用：定量資訊的視覺展示）。

分類變數

對於分類變數，圖表的選擇非常簡單。最基本的圖表只涉及對每個級別的每個資料點進行計數。

• 圖 2.1：分類資料圖表
• 
  (a) 一個簡單的條形圖，顯示不同類別中的資料點數量
• 
  (b) 另一種選擇，適用於高度有序的資料：符號標記資料點數量，線條暗示中間值在概念上是可能的

圖 2.1(a) 將這些計數顯示為條形圖；另一種可能是使用點，如圖 2.1(b) 所示。在性別的情況下，級別的順序並不重要：'男性'或'女性'都可以排在前面。在班級的情況下，級別在圖表中使用了自然順序。在極端情況下，如果中間級別可能是有意義的，或者您希望強調級別之間的模式，則連線點用線可能會比較合理。為了說明目的，圖 2.1(b) 中已經這樣做了，儘管讀者可能質疑它在這種情況下是否合適。

plot(1:length(Gender), Gender, yaxs="n"); axis(2, 1:2, levels(Gender), las=1)

在某些情況下，我們可能對資料點的實際序列感興趣。對於時間序列資料尤其如此，但在其他地方也可能相關。例如，在性別的情況下，資料是按照每個孩子出生的順序記錄的。如果我們認為先前的出生會影響隨後的出生（在這種情況下不太可能，但如果涉及資訊素，則在可能性範圍內），那麼我們可能希望進行符號逐符號繪製。但是，如果我們正在尋找與時間的關聯，那麼雙變數圖表可能更合適***，或者我們對資料的某些特定特徵感興趣（例如重複率），那麼還存在其他可能性（doi:10.1016/j.stamet.2007.05.001）。參見時間序列章節

定量變數

表 2.2：美國 50 個州的陸地面積（km²）

	landArea
阿拉巴馬州	133666
阿拉斯加州	1527463
亞利桑那州	295022
阿肯色州	137538
加利福尼亞州	411012
科羅拉多州	269998
康涅狄格州	12973
特拉華州	5327
佛羅里達州	151669
佐治亞州	152488
夏威夷州	16705
愛達荷州	216411
伊利諾伊州	146075
印第安納州	93993
愛荷華州	145790
堪薩斯州	213062
肯塔基州	104622
路易斯安那州	125673
緬因州	86026
馬里蘭州	27394
馬薩諸塞州	21385
密歇根州	150778
明尼蘇達州	217735
密西西比州	123583
密蘇里州	180485
蒙大拿州	381085
內布拉斯加州	200017
內華達州	286297
新罕布什爾州	24097
新澤西州	20295
新墨西哥州	315113
紐約州	128401
北卡羅來納州	136197
北達科他州	183021
俄亥俄州	106764
俄克拉荷馬州	181089
俄勒岡州	251179
賓夕法尼亞州	117411
羅德島州	3144
南卡羅來納州	80432
南達科他州	199550
田納西州	109411
德克薩斯州	692404
猶他州	219931
佛蒙特州	24887
弗吉尼亞州	105710
華盛頓州	176616
西弗吉尼亞州	62628
威斯康星州	145438
懷俄明州	253596

表 2.3：一個經典的資料集，記錄了 1875-1894 年普魯士軍隊 14 個騎兵團的馬踢造成的意外死亡人數

	deathsPerYear
1875	3
1876	5
1877	7
1878	9
1879	10
1880	18
1881	6
1882	14
1883	11
1884	9
1885	5
1886	11
1887	15
1888	6
1889	11
1890	17
1891	12
1892	15
1893	8
1894	4

定量變數可以用比分類變數更多的方式繪製。下面討論了一些最常見的單變數圖表，使用美國 50 個州的陸地面積作為連續變數的示例，以及一個關於馬踢造成的死亡人數的著名資料集作為離散變數的示例。這些資料在表 2.2 和 2.3 中列出

某些型別的資料包含許多具有相同值的資料點。 這對於計數資料來說尤其如此，其中計數數量很少（例如，後代數量）。

在這些型別的圖中，我們可能希望尋找 3 件事

• 在某種程度上看起來極端的點（這些被稱為異常值）。 異常值通常揭示了資料收集中的錯誤，即使它們沒有，它們也可能對進一步的分析產生不成比例的影響。 如果事實證明它們不是由於明顯的錯誤造成的，則一種選擇是從分析中刪除它們，但這會帶來自身的問題/
• 分佈的形狀和位置（例如，正態，雙峰等）
• 與已知分佈的相似性（QQ）

我們將主要關注變數“landArea”***

圖 2.3：連續定量變數的基本圖

(a) 一維散點圖

(b) 一維散點圖（抖動） (b) 顏色說明上四分位數（紅色）和下四分位數（綠色）

(c) 基本箱線圖。 箱子顯示中位數和上下四分位數，而“須”顯示資料的整個範圍（從最小值到最大值）。 (c) 箱線圖顏色與圖 2.3b 相對應

(d) 複雜的箱線圖。 異常值已從須中排除，並單獨繪製。 箱體中的缺口可以讓我們瞭解我們對中位數值的置信度。

表示定量資料的最簡單方法是在一條線上繪製點，如圖 2.3(a) 所示。 這通常稱為“點圖，儘管有時也用它來描述其他型別的圖（例如圖 2.7）。 為了避免混淆，最好將其稱為一維散點圖。 除了簡單之外，一維散點圖還有兩個優點

1. 資料中存在的所有資訊都保留下來。
2. 異常值很容易識別。 事實上，能夠識別哪些資料點是異常值通常很有用。 一些軟體包允許您以互動方式識別點（例如，透過單擊圖上的點）。 否則，可以對點進行標記，就像在圖 2.3a 中對一些異常點所做的那樣。

對於大型資料集，一維散點圖效果不佳。 圖 2.3(a) 僅包含 50 個點。 即使如此，也很難對資料的總體印象進行總結，（正如諺語所說）“只見樹木，不見森林”。 這部分是因為有些點幾乎重疊，但也因為大量緊密排列的點。 資料的特徵往往可以透過某種方式對其進行總結來更好地探索。

圖 2.3(b) 顯示了一個朝著更佳圖表的步驟。 為了緩解點互相遮擋的問題，它們已被移位，或抖動側向一個小的隨機量。 更重要的是，資料已透過劃分成四分位數來進行總結（並相應地著色，以便於解釋）。 面積最大的州的四分之一被塗成紅色。 最小的州的四分之一被塗成綠色。

更一般地，我們可以談論資料的分位數。 紅線代表 75% 分位數：75% 的點位於其下方。 綠線代表 25% 分位數：25% 的點位於其下方。 這些線之間的距離稱為四分位距（IQR），是資料散佈的一種度量。 粗黑線有一個特殊的名稱：中位數。 它標誌著資料的中間位置，即 50% 分位數：50% 的點位於其上方，50% 的點位於其下方。 分位數相對於其他彙總度量的一個主要優勢是，它們對異常值或尺度變化相對不敏感****。

圖 2.3(c) 是一個廣泛使用的統計彙總圖的彩色版本：箱線圖。 這裡它被著色以顯示與圖 2.3(b) 的對應關係。 箱子標記了資料的四分位數，中位數標記在箱子內。 如果中位數沒有位於箱子內中心位置，這通常表明資料以某種方式傾斜。 箱子兩側的線被稱為“須”，它們總結了位於上四分位數和下四分位數之外的資料。 在這種情況下，須已簡單地擴充套件到觀察到的最大值和最小值。

圖 2.3(d) 是相同資料的更復雜的箱線圖。 這裡，缺口已繪製在箱子上：這些對比較不同箱線圖中的中位數很有用。 須已被縮短，因此它們不包含被認為是異常值的點。 有多種方法可以自動定義這些異常值。 此圖基於一個約定，該約定將異常值視為距離箱子兩側 1.5 倍 IQR 以上的點。 但是，透過目視檢查識別和檢查有趣的點（包括異常值）通常更有資訊量。 例如，在圖 2.1a 中，很明顯阿拉斯加州和（在較小程度上）德克薩斯州是不尋常的大州，但加利福尼亞州（透過此自動程式識別為異常值）並不那麼與眾不同。

圖 2.4：離散定量變數的基本圖

(a) 抖動

(b) 堆疊（或參見圖 2.5a 中的等效線）

(c) 箱線圖對於離散資料也是合理的

(d) 點合併。 這裡每個點的面積（不是寬度或高度）與每個位置的繪圖點數成比例。 很難判斷確切的數字，因此在雪的修改版霍亂圖（第 1 章）等圖中更有用，在這些圖中，根據每個位置的點數賦予位置更大的權重***

在單行上繪圖的一個問題是，如果點重複，那麼***。 這對於離散資料來說尤其成問題。 注意，這些圖沒有特別的理由（或已建立的慣例）必須是垂直的。 圖 2.2 顯示。 堆疊圖（圖 2.4d）類似於直方圖（圖 2.5）。

圖 2.5：直方圖

(a) 直方圖式線圖（與圖 2.4b 比較）	(b) 作為直方圖，年份合併為 2 個 (b) 顏色說明上四分位數（紅色）和下四分位數（綠色）
(c) 連續資料的直方圖 (c) 實際點標記	(d) 更小的箱體寬度 (d) 實際點標記

這提供了另一種將中位數和其他分位數視覺化的方式：將面積分成幾部分***

圖 2.6：密度圖

(a) 核密度圖

(b) 核密度圖（可能會誤導，例如，對於均勻分佈）

我們可以沿著另一個軸將點間隔開。 例如，如果資料集中點的順序有意義，我們可以依次繪製每個點。 這適用於 whatsit 的馬蹄鐵資料。 圖 2.6 按年繪製了資料。

圖 2.7：對資料點進行排序

(a) 簡單的時序圖（即按日期/時間排序）

(b) 分位數圖（按大小排序的相同點） (b) 分位數用相應的箱線圖說明

(c) 經驗累積分佈函式（與 (b) 相同，但軸交換並重新縮放）

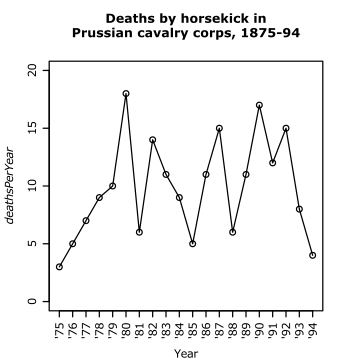我們始終可以做的一件事是按其值對資料點進行排序，首先繪製最小的點，依此類推。 這在圖 2.3b 中可以看到。 如果所有資料點都等距（並且相互排斥****），我們將看到一條直線。 對數變數的圖顯示這種變換在某種程度上使間距均勻。 這被稱為分位數圖，原因如下

當軸交換時，這被稱為經驗累積分佈函式。 未交換的資料對於理解 qq 圖很有用。 也用於理解分位數。 中位數等。

變換

我們可以新增一個尺度斷點，但更好的選擇通常是變換變數。

圖 2.8：對數變換的效果

有時，在不同的尺度（例如對數尺度）上繪圖可能更有資訊量。 我們可以將其視覺化，要麼作為具有非線性（例如對數）軸的圖，要麼作為變換變數的傳統圖（例如，在標準線性軸上繪製 log(my.variable) 的圖）。 圖 2.1(b) 說明了這一點：左側軸標記了州的面積，右側軸標記了州面積的對數。 這種型別的重新縮放可以突出顯示變數的完全不同的特徵。 在這種情況下，很明顯，似乎有一批九個州明顯比大多數州小，而阿拉斯加州仍然顯得異常大，但德克薩斯州在這方面並不顯得那麼不尋常。 這也反映在對數變換變數的自動異常值標記中。

對於較小的數字，它們通常具有更高的解析度。 正如在後面的章節中討論的那樣***，對數尺度對於乘法資料特別有用***。

圖 2.8：平方根變換的效果

還有其他常見的變換，例如，平方根變換（通常用於計數資料）。 如果州大小的限制因素是（例如）州的跨度，或與之相關的因素（例如，從一側到另一側穿越所需的時間），這可能更適合州面積。 圖 2.1c 顯示了資料的平方根重新縮放。 你可以看到，從某種意義上說，這比對數變換不那麼極端……

v·d·e

單變數圖

在 R 中建立粗略的圖非常容易，儘管調整它們以獲得特定外觀可能很耗時。 預設設定通常是合理的。

輸入

stripchart(state.areas, xlab="Area (sq. miles)") #see method="stack" & method="jitter" for others
boxplot(sqrt(state.area))
hist(sqrt(state.area))
hist(sqrt(state.area), 25)
plot(density(sqrt(state.area))
plot(UKDriverDeaths)

qqnorm()
ecdf(

結果

資料集

表中的多個變數。 符號。 大多數包都這樣做。

統計分析：使用 R 簡介/R/資料幀

統計分析：使用 R 簡介/R/讀取資料

雙變數繪圖

定量與定量

散點圖，過度繪圖的問題？ 向日葵圖等等。

定量與分類

小提琴圖（和箱線圖）

分類與分類

馬賽克圖

統計分析：使用 R 簡介/R/雙變數圖

參考文獻

Carifio, J. & Perla, R. (2007)。關於李克特量表和李克特反應格式及其解藥的十個常見誤解、錯誤概念、持久的神話和都市傳說。社會科學雜誌，2，106-116。 http://www.scipub.org/fulltext/jss/jss33106-116.pdf