統計學/數值方法/Excel中的數值計算

本文的目的是評估 MS Excel 在統計程式方面的準確性，並得出結論，MS Excel 是否應該用於（統計）科學目的。

根據文獻，如果將 Excel 用於統計計算，則存在三個主要問題領域。這些是

機率分佈，
單變數統計、方差分析和估計（線性 & 非線性）
隨機數生成。

如果評估統計軟體包的結果，應該考慮到結果的可接受精度應該在雙精度內實現（這意味著如果結果具有 15 位有效數字，則結果被認為是精確的），前提是可靠的演算法也能在雙精度內提供正確的結果。如果可靠的演算法無法以雙精度檢索結果，則不公平地期望該軟體包（已評估）應該實現雙精度。因此我們可以說，評估統計軟體包的正確方法是評估統計計算底層演算法的質量，而不是隻計算結果的有效數字。此外，測試問題必須是合理的，這意味著它們必須能夠透過已知的可靠演算法解決。（McCullough & Wilson, 1999, S. 28）

在後面的部分中，我們對 MS Excel 精確度的判斷將基於經過驗證的值和測試。作為基礎，我們有 Knüsel 的 ELV 軟體用於機率分佈，StRD（統計參考資料集）用於單變數統計、方差分析和估計，最後是 Marsaglia 的 DIEHARD 用於隨機數生成。每個測試和經過驗證的值將在相應部分中解釋。

評估 Excel 結果用於統計分佈

正如我們上面提到的，我們對 Excel 用於機率分佈的計算的判斷將基於 Knüsel 的 ELV 程式，該程式可以計算某些基本統計分佈的機率和分位數。使用 ELV，所有分佈的上尾機率和下尾機率以六位有效數字計算，機率小至 10−100，所有分佈的上分位數和下分位數以六位有效數字計算，尾部機率 P 為 10−12 ≤ P ≤ ½。（Knüsel, 2003, S.1）

在我們的基準測試中，Excel 應該不顯示不精確的數字。如果顯示六位數字，則所有六位數字都應該是正確的。如果演算法僅精確到兩位數字，則應僅顯示兩位數字，以免誤導使用者（McCullough & Wilson, 2005, S. 1245）

在接下來的子部分中，表中的精確值取自 Knüsel 的 ELV 軟體，可接受的精度為單精度，因為即使最好的演算法在大多數情況下也無法實現 15 位有效數字，如果釋出了機率分佈。

正態分佈

Excel 函式：NORMDIST
引數： 平均值 = 0，方差 = 1，x（臨界值）
計算： 尾部機率 Pr X ≤ x，其中 X 表示具有標準正態分佈（平均值為 0，方差為 1）的隨機變數

正如我們在表 1 中看到的，Excel 97、2000 和 XP 遇到了問題，並且不正確地計算了尾部的較小機率（例如，對於 x = -8.3 或 x = -8.2）。但是，這個問題在 Excel 2003 中已得到修復（Knüsel, 2005, S.446）。

逆正態分佈

Excel 函式： NORMINV
引數： 平均值 = 0，方差 = 1，p（X < x 的機率）
計算： x 值（分位數）

X 表示具有標準正態分佈的隨機變數。與上一節中發出的“NORMDIST”函式相反，給定 p 並計算分位數。

如果使用，Excel 97 將以 10 位數字打印出分位數，儘管如果 p 很小，則這些 10 位數字中的任何一個都可能不正確。在 Excel 2000 和 XP 中，Microsoft 試圖修復錯誤，儘管結果並不充分（參見表 2）。但是，在 Excel 2003 中，問題已完全解決。（Knüsel, 2005, S.446）

逆卡方分佈

Excel 函式： CHIINV
引數： p（X > x 的機率），n（自由度）
計算： x 值（分位數）

X 表示具有 n 個自由度的卡方分佈的隨機變數。

舊版 Excel 版本：雖然舊版 Excel 版本顯示十位有效數字，但如果 p 很小，則其中只有很少一部分是準確的（參見表 3）。即使 p 不小，準確的數字也不足以說明 Excel 對這種分佈足夠。

Excel 2003：問題已修復。（Knüsel, 2005, S.446）

逆 F 分佈

Excel 函式： FINV
引數： p（X > x 的機率），n1，n2（自由度）
計算： x 值（分位數）

X 表示具有 n1 和 n2 個自由度的 F 分佈的隨機變數。

舊版 Excel 版本：Excel 以 7 位或更多位有效數字打印出 x 值，儘管如果 p 很小，則這些數字中只有一兩位是準確的（參見表 4）。

Excel 2003：問題已修復。（Knüsel, 2005, S.446）

逆 t 分佈

Excel 函式： TINV
引數： p（|X| > x 的機率），n（自由度）
計算： x 值（分位數）

X 表示具有 n 個自由度的 t 分佈的隨機變數。請注意，|X| 值會導致 2 尾計算。（下尾 & 上尾）

舊版 Excel 版本：Excel 以 9 位或更多位有效數字打印出分位數，儘管如果 p 很小，則這些數字中只有一兩位是準確的（參見表 5）。

Excel 2003：問題已修復。（Knüsel, 2005, S.446）

泊松分佈

Excel 函式： Poisson
引數： λ（平均值），k（案例數）
計算： 尾部機率 Pr X ≤ k

X 表示具有給定引數的泊松分佈的隨機變數。

舊版 Excel 版本：正確地計算了非常小的機率，但對於接近平均值的中心機率（大約在 0.5 範圍內）沒有結果。（參見表 6）

Excel 2003：中心機率已修復。但是，尾部存在不準確的結果。（參見表 6）

對於 λ150 的值，可能會遇到 Excel 的奇怪行為。（Knüsel, 1998, S.375）它甚至對於 0.01 到 0.99 之間的中心範圍內的機率，以及對於不能判斷為過於極端的引數值，都失敗了。

二項分佈

Excel 函式： BINOMDIST
引數： n（= 試驗次數），υ（= 成功機率），k（成功次數）
計算： 尾部機率 Pr X ≤ k

-X 表示具有給定引數的二項分佈的隨機變數

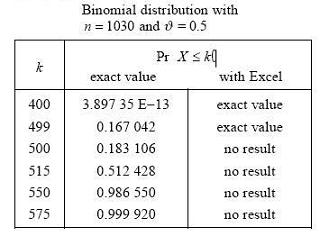
舊版 Excel 版本：正如我們在表 7 中看到的，舊版 Excel 正確地計算了非常小的機率，但對於接近平均值的中心機率沒有結果（與舊版 Excel 版本的泊松分佈相同問題）

Excel 2003：中心機率已修復。但是，尾部存在不準確的結果。（Knüsel, 2005, S.446）。（與 Excel 2003 的泊松分佈相同問題）。

當值 n > 1000 時，可能會遇到 Excel 的這種奇怪行為。(Knüsel, 1998, S.375) 即使對於 0.01 到 0.99 之間的中心範圍內的機率，以及對於不能判斷為過於極端的引數值，它也會失敗。

其他問題

Excel 97、2000 和 XP 在計算超幾何分佈 (HYPERGEOM) 時包含缺陷。對於某些值 (N > 1030)，不會檢索到結果。這在 Excel 2003 中得到阻止，但仍然沒有計算尾部機率的選項。因此，可以計算 Pr {X = k}，但不能計算 Pr {X ≤ k}。(Knüsel, 2005, S.447)
Excel 2003 上的伽馬分佈函式 GAMMADIST 檢索到不正確的值。(Knüsel, 2005, S.447-448)
同樣，Excel 2003 上的逆貝塔分佈函式 BETAINV 也計算出不正確的值 (Knüsel, 2005, S. 448)

評估 Excel 對單變數統計、方差分析和估計 (線性與非線性) 的結果

我們對 Excel 對單變數統計、方差分析和估計的計算的判斷將基於 StRD，StRD 是由美國國家標準與技術研究院 (NIST) 統計工程部設計的，旨在幫助研究人員明確地對統計軟體包進行基準測試。StRD 具有參考資料集（現實世界和生成的資料集），這些資料集具有經過認證的計算結果，可以客觀地評估統計軟體。它包含四套用於統計軟體的數值基準：單變數彙總統計、單因素方差分析、線性迴歸和非線性迴歸，並且每套測試都包含幾個問題。所有問題都具有難度級別：低、平均或高。

透過評估本節中的 Excel 結果，我們將使用 LRE（對數相對誤差），它可以用作統計軟體包結果準確性的得分。可以透過對數相對誤差計算結果中的正確位數。請注意，對於雙精度，計算的 LRE 介於 0 到 15 之間，因為在雙精度中我們最多可以有 15 位正確數字。

公式 LRE

$\lambda =LRE(x)=-log_{10}\left({\frac {|x-c|}{|x|}}\right)$

c：特定測試問題的正確答案（經過認證的計算結果）

x：Excel 對同一問題的答案

單變數統計

Excel 函式： - AVERAGE、STDEV、PEARSON（也稱為 CORREL）

計算（分別）： 平均值、標準差、相關係數

舊版 Excel：使用了一個不穩定的演算法來計算樣本方差和相關係數。即使對於低難度問題（表 8 中帶有字母“l”的資料集），舊版 Excel 也無法正常工作。

Excel 2003：問題已修復，效能可以接受。小於 15 的準確數字並不表示實現不成功，因為即使是可靠的演算法也無法為 StRD 的這些平均難度和高難度問題（表 8 中帶有字母“a”和“h”的資料集）檢索到 15 個正確數字。

單因素方差分析

Excel 函式： 工具 – 資料分析 – 方差分析：單因素 (需要資料分析工具庫)
計算： df、ss、ms、F 統計量

由於方差分析會生成許多數值結果（例如 df、ss、ms、F），因此此處僅介紹最終 F 統計量的 LRE。在評估 Excel 的效能之前，應該考慮一下，一個可靠的單因素方差分析演算法可以為中等難度的題目提供 8-10 位數字的準確度，而對於更高難度的題目可以提供 4-5 位數字的準確度。

舊版 Excel：考慮到數值解，對於難題只提供幾位數字的準確度並不表示軟體不好，但在計算方差分析時，對於中等難度的題目檢索到 0 位正確數字則表示軟體不好。(McCullough & Wilson, 1999, S. 31). 因此，Excel 2003 之前的 Excel 版本僅在低難度問題上表現良好。對於難題，它檢索到零位正確數字。此外，“組內平方和”和“組間平方和”的負結果是使用 Excel 的不良演算法的進一步指標。(見表 9)

Excel 2003：問題已修復 (見表 9)。Simon 9 測試的零位準確度並不令人擔憂，因為當使用可靠的演算法時也會出現這種情況。因此，效能可以接受。(McCullough & Wilson, 2005, S. 1248)

線性迴歸

Excel 函式： LINEST
計算： 線性迴歸所需的所有數值結果

由於 LINEST 為線性迴歸生成許多數值結果，因此僅考慮係數和係數標準誤的 LRE。表 9 顯示了每個資料集的最低 LRE 值，作為鏈條中最薄弱的一環，以便反映最差的估計值 (最小 $\lambda _{\beta }$ -LRE 和 $\lambda _{\sigma }$ -LRE)，Excel 為每個線性迴歸函式做出的估計。

舊版 Excel：要麼不檢查輸入矩陣的近奇異性，要麼檢查不正確，因此對於病態資料集“Filip (h)”的結果不包含一個正確數字。實際上，Excel 應該拒絕該解決方案，並向用戶發出有關資料矩陣的近奇異性的警告。(McCullough & Wilson, 1999, S. 32,33). 但是，在這種情況下，使用者會受到誤導。

Excel 2003：問題已修復，Excel 2003 的效能可以接受。(見表 10)

非線性迴歸

當使用 Excel 求解非線性迴歸時，可以對以下內容進行選擇

導數計算方法：前向 (預設) 或中心數值導數
收斂容差 (預設=1.E-3)
變數縮放 (重新居中)
求解方法 (預設 - GRG2 擬牛頓法)

Excel 的預設引數並不總是能夠產生最佳解決方案 (就像所有其他求解器一樣)。因此，需要提供不同的引數並測試 Excel 求解器以進行非線性迴歸。在表 10 中，A-B-C-D 列是不同非線性選項的組合。由於更改第一個和第四個選項不會影響結果，因此僅更改第二個和第三個引數以進行測試

A：預設估計
B：收斂容差 = 1E -7
C：自動縮放
D：收斂容差 = 1E -7 & 自動縮放

在表 11 中，應用了最低 LRE 原則以簡化評估。(就像線性迴歸一樣)

表 11 中的結果對於每個 Excel 版本（Excel 97、2000、XP、2003）都是相同的。

正如我們在表 11 中看到的，非線性選項組合 A 產生了 21 次，B 產生了 17 次，C 產生了 20 次，D 產生了 14 次“0”精確數字。這表明 Excel 在此方面的效能不足。期望 Excel 能夠找到所有問題的精確解是不公平的，但如果它無法找到結果，則應警告使用者並承諾無法計算出該解。此外，應該強調其他統計軟體包（如 SPSS、S-PLUS 和 SAS）在這些測試中只出現很少的數字精度（0 到 3 次）（McCullough & Wilson，1999，S. 34）。

評估 Excel 的隨機數生成器

許多統計程式使用隨機數，並且期望生成的隨機數確實是隨機的。只應使用具有堅實理論屬性的隨機數生成器。此外，應該對生成的樣本應用統計檢驗，並且只應使用其輸出已成功透過一系列統計檢驗的生成器。（Gentle，2003）

根據上述事實，我們應該透過以下方法評估隨機數生成的質量：

分析隨機數生成的底層演算法。
分析生成器的輸出流。有許多方法可以測試 RNG 的輸出。可以使用靜態測試評估生成的輸出，在這種測試中，生成順序並不重要。這些測試是擬合優度檢驗。評估輸出流的第二種方法是對生成器執行動態測試，其中數字的生成順序很重要。

Excel 的 RNG - 底層演算法

隨機數生成的目的是產生任何給定大小的樣本，這些樣本與來自 U(0,1) 分佈的相同大小的樣本不可區分。（Gentle，2003）為此，可以使用不同的演算法。Excel 的隨機數生成演算法是 Wichmann-Hill 演算法。Wichmann-Hill 是一種適用於常見應用的有用 RNG 演算法，但對於現代需求而言已過時（McCullough & Wilson，2005，S. 1250）。此隨機數生成器的公式定義如下：

$X_{i}=171.X_{i}-1mod30269$

$Y_{i}=172.Y_{i}-1mod30307$

$Z_{i}=170.Z_{i}-1mod30323$

$U_{i}={\frac {X_{i}}{30269}}+{\frac {Y_{i}}{30307}}+{\frac {Z_{i}}{30323}}mod1$

Wichmann-Hill 是一種同餘生成器，這意味著它是一個遞迴算術 RNG，正如我們在上面的公式中看到的。它是三個其他線性同餘生成器的組合，需要三個種子： $X_{0}Y_{0}Z_{0}$ .

週期，就隨機數生成而言，是指在 RNG 開始重複之前可以對 RNG 進行的呼叫次數。因此，具有較長的週期是隨機數生成器的質量指標。生成器的週期必須大於要使用的隨機數的數量。現代應用程式越來越需要更長更長的隨機數序列（例如，用於蒙特卡羅模擬）（Gentle，2003）

良好的 RNG 的最低可接受週期是 $2^{60}$ ，Wichmann-Hill RNG 的週期是 6.95E+12（≈ $2^{43}$ ）。除了這種不可接受的效能之外，Microsoft 聲稱 Wichmann-Hill RNG 的週期為 10E+13。即使 Excel 的 RNG 具有 10E+13 的週期，它仍然不足以成為一個可接受的隨機數生成器，因為該值也小於 $2^{60}$ 。（McCullough & Wilson，2005，S. 1250）

此外，眾所周知，Excel 的 RNG 在 RNG 執行多次後會產生負值。然而，Wichmann-Hill 隨機數生成器的正確實現應該只產生 0 到 1 之間的數值。（McCullough & Wilson，2005，S. 1249）

Excel 的 RNG - 輸出流

正如我們上面所討論的，僅僅討論隨機數生成的底層演算法是不夠的。在評估此隨機數生成器的質量時，還需要對隨機數生成器的輸出流進行一些測試。因此，隨機數生成器應該產生透過一些隨機性測試的輸出。Marsaglia 制定了一套這樣的測試，稱為 DIEHARD。良好的 RNG 應該通過幾乎所有的測試，但正如我們在表 12 中看到的，Excel 只能透過 11 個測試（7 個失敗），儘管 Microsoft 已宣佈為 Excel 的 RNG 實現了 Wichmann-Hill 演算法。然而，我們知道 Wichmann-Hill 能夠透過 DIEHARD 的 16 個測試（McCullough & Wilson，1999，S. 35）。

由於前面和本節中解釋的原因，我們可以說 Excel 的效能不足（因為週期長度、Wichmann Hill 演算法的錯誤實現，該演算法已經過時，DIEHARD 測試結果）

結論

舊版本的 Excel（Excel 97、2000、XP）

在以下分佈上表現出較差的效能：正態、F、t、卡方、二項式、泊松、超幾何
在以下計算中獲得不充分的結果：單變數統計、方差分析、線性迴歸、非線性迴歸
具有不可接受的隨機數生成器

基於以上原因，我們建議避免使用Excel 97、2000、XP進行（統計）科學計算。

儘管Excel 2003修復了一些錯誤，但仍然建議避免使用Excel進行（統計）科學計算，因為：

它在以下分佈上的表現不佳：二項分佈、泊松分佈、伽馬分佈、貝塔分佈
非線性迴歸結果不準確
隨機數生成器過時。

參考文獻

Gentle J.E. (2003) 隨機數生成與蒙特卡羅方法第二版。紐約施普林格出版社
Knüsel, L. (2003) 統計分佈計算 ELV程式文件第二版。 http://www.stat.uni-muenchen.de/~knuesel/elv/elv_docu.pdf 獲取時間 [2005年11月13日]
Knüsel, L. (1998). 關於Microsoft Excel 97中統計分佈的準確性。計算統計與資料分析 (CSDA)，第26卷，375-377。
Knüsel, L. (2002). 關於Microsoft Excel XP在統計用途上的可靠性。計算統計與資料分析 (CSDA)，第39卷，109-110。
Knüsel, L. (2005). 關於Microsoft Excel 2003中統計分佈的準確性。計算統計與資料分析 (CSDA)，第48卷，445-449。
McCullough, B.D. & Wilson B. (2005). 關於Microsoft Excel 2003中統計程式的準確性。計算統計與資料分析 (CSDA)，第49卷，1244 – 1252。
McCullough, B.D. & Wilson B. (1999). 關於Microsoft Excel 97中統計程式的準確性。計算統計與資料分析 (CSDA)，第31卷，27– 37。
PC雜誌，2004年4月6日，第71頁*