材料力學/未分類主題
在工程力學課程中,我們使用力的平衡來求解各個構件中的力。但是,在某些情況下,這是不可能的,這些問題被認為是靜不定問題。它們需要一些本構方程才能完全求解,而胡克定律就是這樣一個方程。
例如,考慮一個兩端固定的柱子,並在中心施加一個載荷P。現在,我們知道在兩端作用著反力R1和R2。此外,使用力的平衡,我們有R1 + R2 = P。這裡我們有兩個未知數,R1和R2,但只有一個方程。我們可以應用胡克定律,以及位移Δ1和Δ2,其中Δ1 = R1L/2AE和Δ2 = R2L/2AE。第二個方程是Δ1 = Δ2,因為支座是固定的。因此,我們可以解決這個問題。
考慮一根具有不同橫截面積Ai和長度Li的杆,使得每一截面都有一個等效的彈簧常數AiE/Li。如果每個節點(面積變化處)的力為Fi,那麼我們可以根據每個節點的位移和每一段的彈簧常數寫出關於力Fi的方程。如果梁兩端固定,則力只能作用於其他節點。
在一般情況下,如果您有載荷作用於連線的細杆上,您可以使用這種方法來求解力和變形。整個結構可以被離散化,並且節點被編號,以便我們得到矩陣[kij]。
這種將複雜問題分解成大量簡單問題的方法稱為有限元法。
各個部分稱為單元,在上述情況下,我們使用了線單元。對於一般2-D問題,我們至少需要使用三角形單元。典型問題的矩陣將包含數百個這樣的單元,矩陣的大小與單元的數量相同。但是,由於大多數成員都是零,因此該矩陣稱為稀疏矩陣,並且可以比您在數學課程中遇到的典型矩陣快得多地求解。
到目前為止,我們一直在處理作用在梁兩端的點載荷。我們假設應力與σav = P/A相同。但是,這在載荷作用點附近是不正確的。聖維南原理(由法國彈性學家聖維南提出)指出,遠離載荷作用點的應力不受結構在載荷作用點附近精確行為的影響。在所示的圖中,這意味著儘管 A-A 處的應力場可能難以計算,但在 B-B 處,應力可以近似為 P/A。S-V 原理與多年的實驗和分析相一致,但尚未得到證明。
到目前為止,我們假設橫截面中所有點的應力都相同,並且大體上是正確的。但是,在點載荷和不連續性附近,應力會增加。峰值載荷是根據先前方法計算的平均應力的函式。正確的峰值載荷只能透過有限元分析等方法獲得。但是,已經為幾種典型場景釋出了圖表。如前所述,峰值應力σp是平均應力σav的函式。現在,我們有σp = K×σav,其中K稱為應力集中係數,可以從表格中查閱常見場景。應力集中係數的研究也是一項設計指南,並指示了在現實世界中應避免的特徵型別。例如,圓角半徑的應力集中係數在r < 0.1 d之外迅速增加,因此您應該為您的軸指定較大的圓角半徑或消除直徑的變化。
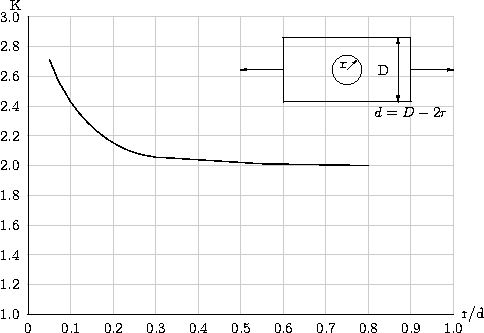
上圖顯示了帶孔板的應力集中比K的可能值。最窄截面的應力是根據d = D − 2r計算的,其中r是孔的半徑,D是板的寬度。可以看出,應力集中直到大約r/d = 0.3才顯著。
請注意,由於材料的塑性流動,區域性應力可能不如應力集中係數所暗示的那樣高,因為應力集中分析是針對彈性流動的。
泊松比顯示當一個方向發生一定變化時,另一個方向上發生的尺寸變化量。每個方向上的應變是所有應變的疊加——直接應變和由於泊松比引起的應變。因此,我們可以將廣義胡克定律表述如下
請注意,這些方程僅適用於各向同性材料(鋼、鋁、銅等),其彈性特性在所有方向上都相同。
考慮一個元素,其上分別沿x和y方向作用著應力σ1和σ2。現在進一步考慮σ1 = σ和σ2 = −σ。
剪下模量可以用楊氏模量表示
考慮一個正在經歷壓縮的物體,因此其應變分別為εx、εy和εz。體積的分數變化因此為εx + εy + εz。應用胡克定律的廣義形式,我們得到,體積模量k由下式給出:
在不同於周圍環境的壓力下輸送、儲存或接收流體的容器、罐和管道稱為壓力容器。壓力容器通常是薄壁結構,包含高壓流體。設計決策是為給定的最大壓力p找到壓力容器厚度t的值。由於厚度遠小於容器半徑r,因此內半徑和外半徑被認為相等。對於縱向,我們有壓力πr2p產生的力。這由壁中產生的應力平衡,作用在圓的周長2πrtσ上。因此縱向的應力為pr/2t。對於切向,壓力力為π2rl,應力力為2tlσ。應力為pr/t。
當對於某個特定屬性,材料在測量資料中顯示出較大的離散度(例如,脆性材料或厚度變化較大的螺紋的強度測量結果),可以透過基於三引數威布林統計分析測量資料來獲得該屬性的特徵值或最弱環節。