面積和體積 是空間幾何學的一個主題,它處理三維幾何體積的體積和麵積的性質、特徵、應用和計算。三維體積是具有三個維度(長度、寬度、高度)的物體。
旋轉、截面、切割、三維繪圖、體積的擴充套件繪圖、封閉、體積和麵積是該主題的重要元素。
幾何體積分為兩類
稜柱、球體、錐體等幾何體積。
非幾何體積 體積 :物體所佔空間的大小稱為體積。體積單位等於立方單位。體積是三維空間的量,它由特定邊界限制,例如,它是由物質(固體、氣體、液體、等離子體)或其形狀所佔的空間。體積是 SI 的子單位,它是米的三次方(立方米)。容器的體積等於裝滿它的液體的體積。為了計算某些三維形狀的體積,存在特定關係,這些關係對於具有幾何規律的簡單形狀來說是簡單的關係。對於沒有簡單關係來計算體積的複雜形狀,可以透過積分方法獲得體積。一維形狀(如線)或二維形狀(如平面)的體積為零。
面積 :它是一種計算三維物體表面值和二維物體內部值的量。面積單位等於平方單位。面積是表示平面或曲面上區域大小的量。平面區域或“平面面積”是指平面層或層的面積,而“表面積”是指三維物體開放表面或邊界的面積。面積可以理解為形成形狀模型所需的給定厚度的材料量,或者用一層塗料覆蓋表面所需的塗料量。這種二維類比是一條曲線(一維概念)的長度或一個固體(三維概念)的體積。
非幾何體積 =非幾何體積是體積難以獲得的複雜體積。但它們的面積可以獲得,但有點複雜。為了獲得非幾何體積,我們首先在燒杯中倒入水。在我們用它裝滿水並測量體積後,我們將非幾何物體放入水中。水會上升,然後我們將非幾何體積使水上升的體積與之前測定的水體積相減,然後測量並記錄其體積。
幾何體積 =幾何體積是可以為其寫出表面積和體積公式的物體。我們可以透過分析和測量相應分量的體積,透過模式查詢方法找到這些幾何物體的體積。然後透過總結和公式化,我們可以得到其體積的公式。為了找到它的面積,我們首先透過分析和以連續和離散的方式繪製形狀來計算其分量的面積,並透過分析寫出其公式。
例子 = 球體、錐體、稜柱、多面體、圓柱體、圓錐體和立方體、四面體、平行四邊形
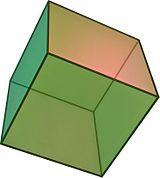
說明 1:規則多面體(六面體)立方體有一個正方形面,它有兩個正方形底面,因此立方體是一個規則的稜柱-多面體體積。
說明 2:四面體是一個金字塔,也是一個多面體,其底面和側面為等邊三角形。因此,四面體被認為是一個金字塔-多面體體積,也是一種柏拉圖立體。
要點 3:平行四邊形是一個具有側面和為六邊形的稜柱體積,其側面平行。因此,平行四邊形是一個稜柱-多面體體積。
稜柱的定義 :稜柱是一個具有兩個底面、側面、頂點和邊的體積。稜柱的面是矩形,面的數量等於底面的邊數,頂點的數量是面的數量的兩倍,邊的數量是稜柱面的三倍。稜柱的面的數量透過公式 n+2 獲得,因為稜柱中心的面的數量總是比側面的數量多兩個,因為另外兩個面是稜柱的底面。在另一個平面中)和 n 個其他面,這些面必然都是平行四邊形,並將兩個 n 邊形的對應頂點連線起來。所有平行於底面的橫截面都是相同的。稜柱根據其底邊數命名;因此,例如,具有五邊形底面的稜柱稱為五邊形稜柱。稜柱與金字塔的定義是,稜柱與金字塔相同,但其頂點位於無窮遠處。
錐體的定義 :錐體是一個體積,其面在一個點處相交,並且其面為三角形,其底面為三角形。邊的數量是底面。實際上,錐體是透過將空間中的一個點連線到平面上所有封閉形狀點的點而建立的三維形狀。該點稱為錐體頂點,該平面形狀稱為錐體底面。錐體的底面是一個任意的多邊形,其他面是連線到頂點的等邊三角形。連線頂點和底面的垂線稱為錐體的高度。在世界上最著名的金字塔形結構中,我們可以提到埃及的三座金字塔。
球體的定義 :球體是三維空間中的一個完全圓形的幾何物體。例如,球體是一個球體。球體就像二維空間中的圓一樣,在三維空間中的一個點周圍完全對稱。球體表面上的所有點都與球體中心相距相等。這些點到球體中心的距離稱為球體的半徑,用字母 r 表示。球體兩側的最長距離(穿過球體)稱為球體的直徑。球體的直徑也穿過其中心,因此其大小是半徑的兩倍。球體是空間中的一組點,具有圓形底面和半徑,它是一個規則的多面體。球體是半圓和一個圓繞其直徑旋轉一週的結果,在圓周上旋轉 180 度,在半圓周上旋轉 360 度。我們根據其面積的劃分將球體的面劃分為幾個度數,它為 360 度。
圓柱體的定義:圓柱體是一種底面為圓形的稜柱體。在幾何學中,圓柱體是一種空間曲線底面,其表面由一組點形成。圓柱體的邊是不可確定的,因為它的底面是圓形的。也就是說,可以認為圓柱體的側面、面、頂點、邊依次為3n、2n、n+2、n。微分幾何中的圓柱體被繪製為生成線為一組平行線的曲面。圓錐體中圓柱體的定義與圓錐體相同,但其頂點在無窮遠處。圓柱體是由一個矩形繞其一側(長、寬)旋轉360度得到的。
圓錐體的定義:圓錐體是一種底面為圓形的錐體,圓錐體是一種三維幾何圖形,從其平坦的底面(圓錐體截面)到頂點,緩慢或快速(取決於底面和高度)地變窄。更確切地說,它是由一個底平面(圓錐體截面)和一個側面所包圍的固體形狀,該側面是連線圓錐體頂點與底面周圍點的直線的軌跡。圓錐體一詞有時指的是該固體的頂點,有時僅指其側面。圓錐體可以是直立的或傾斜的。必須提到的是,具有特定截面積和特定高度的斜圓錐的體積等於具有相同面積和特定高度的直圓錐的體積。由直角三角形繞其一邊(鄰邊)旋轉360度得到的圓錐體。
多面體的定義:多面體是三維空間中的一個立體幾何體,具有平面面(每個面在一個平面內)和位於直線上的邊或稜。迄今為止,還沒有為它提供單一的定義。四面體是一種金字塔,立方體是六面體的例子。多面體可以是凸的或非凸的。金字塔和稜柱等多面體可以透過擠壓二維多邊形來製作。具有規則面和等角形狀的凸多面體只有有限個,包括柏拉圖立體和阿基米德立體。一些阿基米德立體可以透過切割柏拉圖立體的頂部金字塔來製作。由於構造的簡單性,多面體在大多數建築作品中使用,例如測地線圓頂和金字塔。近年來,由於形狀的使用,對多面體表面的興趣不斷增加。一些緊湊的分子和原子,特別是晶體結構和柏拉圖烴,以及一些徑向具有與柏拉圖立體相似的形狀。柏拉圖立體也被用於製作骰子。多面體具有不同的特徵和型別,並被置於不同的對稱群中。其他多面體可以透過對任何多面體進行操作來建立。其中一些彼此之間存在關係。多面體自石器時代以來就一直受到人們的關注。球體也被認為是多面體家族的一部分。立方體、四面體、平行四邊形都是幾何體,也被認為是多面體。
立方體的體積: V = a 3 {\displaystyle V=a^{3}\;}
立方體的表面積: V = 6 a 2 {\displaystyle V=6a^{2}\;}
四面體的體積: V = 2 12 a 3 {\textstyle V={{\sqrt {2}} \over 12}a^{3}\,}
四面體的表面積: V = 3 a 2 {\displaystyle V={{\sqrt {3}}a^{2}\,}}
正八面體的體積
V = 2 3 a 3 {\displaystyle V={\frac {2}{3}}a^{3}}
正八面體的表面積
V = 2 a 2 3 {\displaystyle V={2a^{2}{\sqrt {3}}\,}}
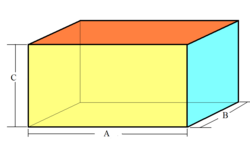
長方體的體積: V = a b c {\textstyle {V=abc}}
長方體的表面積: A = 2 a b + 2 a c + 2 c b {\textstyle A=2ab+2ac+2cb}
稜柱體的體積: V = S h {\displaystyle V=Sh}
多邊形底稜柱體的體積: V = n 4 h a 2 cot π n {\displaystyle V={\frac {n}{4}}ha^{2}\cot {\frac {\pi }{n}}}
多邊形底稜柱體的表面積: A = n 2 a 2 cot π n + n a h {\displaystyle A={\frac {n}{2}}a^{2}\cot {\frac {\pi }{n}}+nah}
圓柱體的體積: V = π r 2 h {\displaystyle {\displaystyle V=\pi r^{2}h}}
圓柱體的側面積: A = P h + 2 S {\displaystyle A=\ Ph+2S}
圓柱體面積: A = 2 π r ( r + h ) {\displaystyle A=2\pi r(r+h)\,\!}
金字塔的體積: V = 1 3 S h {\displaystyle V={\displaystyle {\frac {1}{3}}Sh}}
圓錐的體積: V = 1 3 π r 2 h {\displaystyle V={\frac {1}{3}}\pi r^{2}h}
金字塔的面積: B + P L 2 {\displaystyle B+{\frac {PL}{2}}\,\!}
圓錐的面積: π r ( r + l ) {\displaystyle \pi r(r+l)\,\!}
球體的體積: V = 4 3 π r 3 {\displaystyle V={\frac {4}{3}}\pi r^{3}}
球體的面積: 4 π r 2 or π d 2 {\displaystyle 4\pi r^{2}\ {\text{or}}\ \pi d^{2}\,\!}
球形體積: 4 3 π r 2 h {\displaystyle {4 \over 3}\pi r^{2}h}
橢球體積: 4 3 π a b c {\displaystyle {4 \over 3}\pi abc}
球形面積= A = 4 π a b {\displaystyle {A=4\pi ab}}
橢圓面積=: A = 2 π a 2 ( 1 + c a e arcsin e ) {\displaystyle A=2\pi a^{2}\left(1+{\frac {c}{ae}}\arcsin e\right)}
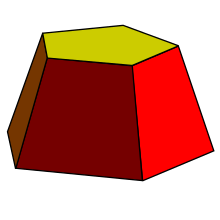
不完整金字塔的體積: V = 1 3 h ( a 2 + a b + b 2 ) . {\displaystyle V={\tfrac {1}{3}}h\left(a^{2}+ab+b^{2}\right).}
不完整金字塔的面積: A = n 4 [ ( a 1 2 + a 2 2 ) cot π n + ( a 1 2 − a 2 2 ) 2 sec 2 π n + 4 h 2 ( a 1 + a 2 ) 2 ] {\displaystyle A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]}
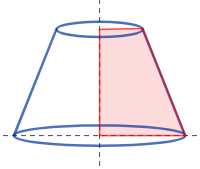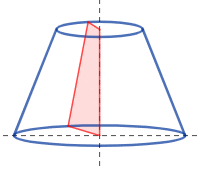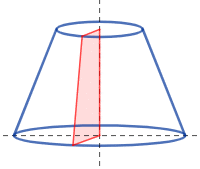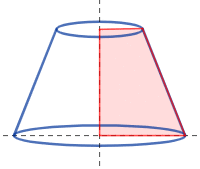
不完全圓錐體積: V = π 3 h ( r 2 + r r ′ + r ′ 2 ) . {\displaystyle {\displaystyle V={\tfrac {\pi }{3}}h\left(r^{2}+rr'+r'^{2}\right).}}
不完全圓錐表面積: Total surface area = = π ( ( r 1 + r 2 ) ( r 1 − r 2 ) 2 + h 2 + r 1 2 + r 2 2 ) {\displaystyle {\displaystyle {\begin{aligned}{\text{Total surface area}}&=\\&=\pi \left(\left(r_{1}+r_{2}\right){\sqrt {\left(r_{1}-r_{2}\right)^{2}+h^{2}}}+r_{1}^{2}+r_{2}^{2}\right)\end{aligned}}}}
圓環體積: V = 2 π 2 R r 2 = ( π r 2 ) ( 2 π R ) . {\displaystyle V=2\pi ^{2}Rr^{2}=\left(\pi r^{2}\right)\left(2\pi R\right).\,}
圓環面積: A = 4 π 2 R r = ( 2 π r ) ( 2 π R ) {\displaystyle A=4\pi ^{2}Rr=\left(2\pi r\right)\left(2\pi R\right)\,}
平行六面體體積: V = a b c K {\displaystyle V=abc{\sqrt {K}}}
平行六面體表面積: 2 ( a h + b h ′ + c h ″ ) {\displaystyle 2{(ah+bh'+ch'')}}
正多面體面積
A = n ( 1 4 n ′ a 2 cot π n ′ ) {\displaystyle A=n({\tfrac {1}{4}}n'a^{2}\cot {\frac {\pi }{n'}})}
多面體體積: 1 3 | ∑ F ( Q F ⋅ N F ) Area ( F ) | , {\displaystyle {\frac {1}{3}}\left|\sum _{F}(Q_{F}\cdot N_{F})\operatorname {Area} (F)\right|,}
表面積與體積之比,用 sa/vol 或 SA:V 表示,是指物體或物體集合的每個體積單位所對應的表面積。在涉及固體物質的化學反應中,表面積與體積之比是一個重要的因素,它表明化學反應正在進行。表面積與體積之比或 SA:V 是一個公式,它表示體積與總表面積之比,其數值在不同的幾何體中是不同的。SA:V 比值取決於半徑的大小或幾何體的大小。
V/S立方體比例: a 6 {\displaystyle {\frac {a}{6}}}
四面體 V/S 比例: 2 12 a 3 2 a 2 3 {\displaystyle {\frac {{{\sqrt {2}} \over 12}a^{3}}{2a^{2}{\sqrt {3}}}}}
V/S 比例: S h P h + 2 s {\displaystyle {\frac {Sh}{Ph+2s}}}
圓柱體的 V/S 比例: π r 2 h 2 π r 2 + 2 π r h {\displaystyle {\frac {\pi r^{2}h}{2\pi r^{2}+2\pi rh}}}
金字塔的 V/S 比例: 1 3 S h N 2 B h + S {\displaystyle {\frac {{\frac {1}{3}}Sh}{{\frac {N}{2}}Bh+S}}}
圓錐的 V/S 比例: 1 3 π r 2 h π r 2 + π r L {\displaystyle {\frac {{\frac {1}{3}}\pi r^{2}h}{\pi r^{2}+\pi rL}}}
球體的 V/S 比例= r 3 {\displaystyle {\frac {r}{3}}}
一個三維球體的表面積與體積比值 (SA:V) 值圖,顯示了球體半徑增大。球體半徑與比例成反比關係。 球體是一個三維物體,形狀為球形(在本主題中,球體上的大部分面積(面積)是需要的,而不是它內部的體積)。球體可以存在於任何需要的維度,並且通常被稱為 n 維球體,其中 n 是球體的維度數。對於典型的三維球體,SA:V 可以使用面積和體積的標準公式計算;其中面積 i s S = 4 π r 2 {\displaystyle isS=4\pi r^{2}} i s V = ( 4 / 3 ) π r 3 {\displaystyle isV=(4/3)\pi r^{3}}
上述論點可以擴充套件到 n 維球體,並且可以寫出體積和表面積的一般關係,如下所示
V = r n π n 2 Γ ( 1 + n / 2 ) {\displaystyle V={\frac {r^{n}\pi ^{\frac {n}{2}}}{\Gamma (1+n/2)}}} S = n r n − 1 π n 2 Γ ( 1 + n / 2 ) {\displaystyle S={\frac {nr^{n-1}\pi ^{\frac {n}{2}}}{\Gamma (1+n/2)}}}
比率 V S {\displaystyle {\frac {V}{S}}} n r − 1 {\displaystyle nr^{-1}}
這些主題是對列表的部分證明,以及對其公式證明的參考。要檢視完整的證明,您應該閱讀補充數學中幾何部分關於三維幾何形狀的部分。
立方體的體積像長方體的體積一樣,但由於立方體的邊是相等的,它被放置在它邊的三次方上。
V = S . H = ( a 2 ) . a = a 3 {\displaystyle V=S.H=(a^{2}).a=a^{3}}
立方體的表面積也可以用不同的方法證明,我們知道立方體有六個正方形的面,它們都是規則的四邊形,它的總面積是根據立方體的六個正方形面的總和得到的。立方體的總面積,就像立方體的體積一樣,是透過稜柱公式得到的,並且根據稜柱的總面積來證明。
V = P . H + 2 S = 4 a 2 + 2 a 2 = 6 a 2 {\displaystyle V=P.H+2S=4a^{2}+2a^{2}=6a^{2}}
平行六面體的體積是根據三個向量 a、b、c 得到的,這三個向量以行列式的形式確定。但首先,它應該用三角函式計算,然後寫成行列式。
S = | a | ⋅ | b | ⋅ sin γ = | a × b | {\displaystyle S=\left|\mathbf {a} \right|\cdot \left|\mathbf {b} \right|\cdot \sin \gamma =\left|\mathbf {a} \times \mathbf {b} \right|}
h = | c | ⋅ | cos θ | {\displaystyle h=\left|\mathbf {c} \right|\cdot \left|\cos \theta \right|}
計算完成後,我們將工作寫成行列式的形式。
V = | det [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] | . {\displaystyle V=\left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right|.}
a → = ( a 1 , a 2 , a 3 ) {\displaystyle {\vec {a}}=(a_{1},a_{2},a_{3})} b → = ( b 1 , b 2 , b 3 ) {\displaystyle {\vec {b}}=(b_{1},b_{2},b_{3})} c → = ( c 1 , c 2 , c 3 ) {\displaystyle {\vec {c}}=(c_{1},c_{2},c_{3})} 平行六面體的體積是這樣的。
V = | ( a → . b → ) . c → | = a 1 b 1 c 1 + a 2 b 2 c 2 + a 3 b 3 c 3 {\displaystyle V=|({\vec {a}}.{\vec {b}}).{\vec {c}}|=a_{1}b_{1}c_{1}+a_{2}b_{2}c_{2}+a_{3}b_{3}c_{3}}
稜柱的體積,如果 s 是底面積,h 是高,它的體積是: V = S h {\displaystyle V=Sh}
如果 p 是底面的周長,h 是高,稜柱的側面積可以相應地寫成。
S = P h {\displaystyle S=Ph}
如果 s 是底面積,稜柱的總面積可以根據這個公式寫成 S = P h + 2 s {\displaystyle S=Ph+2s}
圓柱是幾何學中基本曲面形狀之一,其外表面是一組到直線距離相等的點。這條線的名稱為中心軸。這種空間形狀的兩端由垂直於封閉圓柱體軸線的兩塊板封閉。圓柱體的表面積和體積在很早以前就為數學家所知。
圓柱體的體積是根據稜柱體的體積計算的。
V = S . H = π R 2 H {\displaystyle V=S.H=\pi R^{2}H}
四面體 平行六面體 長方體 稜柱體 稜錐 圓錐 不完整稜錐 球體 







































![{\displaystyle A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c9ba44195955a9024eca9605b00b44cdbe785a)
































