補充數學/正多邊形

在歐幾里得幾何中，"正多邊形"是指所有角和邊都相等的 多邊形。正多邊形可以是凸多邊形或星形多邊形。在極限情況下，如果周長保持不變，一系列邊數不斷增加的正多邊形會變成圓形；如果邊長保持不變，則會變成無窮邊形。

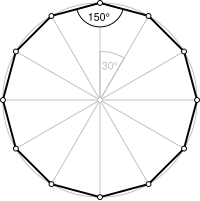十二邊形

周長和麵積

周長

正多邊形的周長是透過正多邊形邊數乘以正多邊形邊長來計算的。

周長透過以下關係式得出：$P=a_{1}+a_{2}+...+a_{n}=(n.a)=na$ 其中 n 等於正多邊形的邊數，a 等於正多邊形的邊長。

面積

正多邊形的面積是基於三角函式關係計算得到的。正多邊形的面積基於其由 1x1 的正方形組成，邊數為 n，且基於圓周率，邊數根據 cotangent 以圓周率的形式三角函式擴充套件，得到正多邊形的邊數除以 1。

正多邊形的面積可寫成如下形式

$A={\frac {1}{4}}n.a^{2}\cot({\frac {\pi }{n}})$

這裡，π 是以弧度表示的（等於 180°）。

三角函式方法計算正方形面積

由於正方形是一種正多邊形，其面積也可以用三角函式方法計算正多邊形的面積公式得出，公式如下：${\frac {1}{4}}na^{2}\cot {\frac {\pi }{n}}=a^{2}\cot {\frac {\pi }{4}}=a^{2}.({\sqrt {1}})=1.a^{2}=a^{2}$ 這裡

${\frac {1}{4}}na^{2}={\frac {1}{4}}4a^{2}=a^{2}$

$\cot {\frac {\pi }{4}}=1$

因此，平行正方形的面積等於其邊長的平方。

其他面積公式

邊長為 a、外接圓半徑為 R、內接圓半徑為 r、周長為 p 的 "n-" 正多邊形的面積可透過以下關係式得出

(角度以弧度表示)。

$A={\tfrac {1}{2}}nar={\tfrac {1}{2}}pr={\tfrac {1}{4}}na^{2}\cot {\tfrac {\pi }{n}}=nr^{2}\tan {\tfrac {\pi }{n}}={\tfrac {1}{2}}nR^{2}\sin {\tfrac {2\pi }{n}}$

其中 R 等於

$R={\frac {s}{2\sin \left({\frac {\pi }{n}}\right)}}={\frac {a}{\cos \left({\frac {\pi }{n}}\right)}}$