支援向量機

支援向量機 (SVM) 是一組相關的監督學習方法，用於分析資料和識別模式，用於分類和迴歸分析。原始的 SVM 演算法由弗拉基米爾·瓦普尼克發明，而目前標準的實現形式 (軟間隔) 由科林娜·科特斯和弗拉基米爾·瓦普尼克提出。標準的 SVM 是一種非機率二元線性分類器，也就是說，它預測對於每個給定的輸入，該輸入屬於兩個可能的類別中的哪一個。由於 SVM 是一種分類器，因此給定一組訓練樣本，每個樣本都標記為屬於兩個類別之一，SVM 訓練演算法構建一個模型來預測新樣本是否屬於一個類別或另一個類別。直觀地說，SVM 模型是將樣本表示為空間中的點，對映的方式使得不同類別的樣本之間存在清晰的間隔，這個間隔儘可能寬。然後將新的樣本對映到相同的空間，並根據它們落在間隔的哪一邊來預測它們屬於哪個類別。

更正式地說，支援向量機在一個高維或無限維空間中構建一個超平面或一組超平面，可用於分類、迴歸或其他任務。直觀地說，可以透過距離任何類別最近的訓練資料點距離最大的超平面 (稱為函式間隔) 來實現良好的分離，因為通常間隔越大，分類器的泛化誤差越低。

儘管原始問題可能在一個有限維空間中表述，但通常情況下，在那個空間中，要區分的集合不是線性可分的。因此，有人提出將原始有限維空間對映到一個更高維的空間，假設在這個空間中分離更容易。SVM 方案使用對映到一個更大的空間，以便能夠以原始空間中的變量表示輕鬆計算交叉乘積，從而使計算負載合理。較大空間中的交叉乘積由核心函式$K(x,y)$ 定義，該函式可以根據問題進行選擇。較大空間中的超平面被定義為與該空間中的某個向量交叉乘積為常數的點的集合。定義超平面的向量可以被選擇為特徵向量影像的線性組合，其引數為$\alpha _{i}$，這些特徵向量影像出現在資料庫中。有了這種超平面選擇，對映到超平面中的特徵空間中的點 x 由以下關係定義：$\sum _{i}{\alpha _{i}K(x_{i},x)}=constant$ 請注意，如果$K(x,y)$ 隨著 $y$ 距離 $x$ 越來越遠而變小，則上述總和中的每個元素都衡量了測試點 $x$ 與相應資料庫點 $x_{i}$ 的相對接近程度。這樣，上面核心的總和可以用來衡量每個測試點與源自要區分的集合中的一個或另一個的資料庫點的相對接近程度。請注意，對映到任何超平面中的點 $x$ 的集合可能相當複雜，因此允許在原始空間中與凸形相去甚遠的集合之間進行更復雜的區分。

動機

H3（綠色）無法將 2 類分開。H1（藍色）可以，但邊距很小，而 H2（紅色）則具有最大邊距。

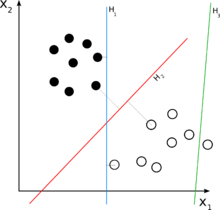
統計分類|分類資料是機器學習中的一項常見任務。假設一些給定的資料點分別屬於兩個類別之一，目標是確定一個新資料點屬於哪個類別。在支援向量機的情況下，資料點被視為一個 $p$-維向量（$p$ 個數字的列表），我們想知道是否可以用一個 $p-1$-維超平面將這些點分開。這被稱為線性分類器。存在許多可能對資料進行分類的超平面。一個合理的最佳超平面選擇是代表兩類之間最大分離或邊距的超平面。因此，我們選擇超平面，使其到兩側最近資料點的距離最大化。如果這樣的超平面存在，它被稱為最大邊距超平面，它定義的線性分類器被稱為最大邊距分類器。

形式化

我們得到了一些訓練資料 ${\mathcal {D}}$，它是一個包含n個點的集合，這些點的形式為

${\mathcal {D}}=\left\{(\mathbf {x} _{i},c_{i})\mid \mathbf {x} _{i}\in \mathbb {R} ^{p},\,c_{i}\in \{-1,1\}\right\}_{i=1}^{n}$

其中c_i 為 1 或 -1，表示點 $\mathbf {x} _{i}$ 所屬的類別。每個 $\mathbf {x} _{i}$ 都是一個 $p$-維實數|實向量。我們想要找到將 $c_{i}=1$ 的點與 $c_{i}=-1$ 的點分開的最大邊距超平面。任何超平面都可以寫成滿足以下條件的點 $\mathbf {x}$ 的集合：

SVM 訓練樣本來自兩個類別，其最大邊距超平面和邊距。邊距上的樣本稱為支援向量。

$\mathbf {w} \cdot \mathbf {x} -b=0,\,$

其中 $\cdot$ 表示點積。向量 ${\mathbf {w} }$ 是一個表面法線 | 法向量：它垂直於超平面。引數 ${\tfrac {b}{\|\mathbf {w} \|}}$ 決定了超平面相對於原點沿法向量 ${\mathbf {w} }$ 的偏移。

我們想要選擇 ${\mathbf {w} }$ 和 $b$ 來最大化間隔，或者說最大化兩個平行超平面之間的距離，這兩個超平面儘可能地遠離彼此，同時仍然將資料分開。這些超平面可以用以下方程描述：

$\mathbf {w} \cdot \mathbf {x} -b=1\,$

和

$\mathbf {w} \cdot \mathbf {x} -b=-1.\,$

注意，如果訓練資料是線性可分的，我們就可以選擇間隔的兩個超平面，使得它們之間沒有點，然後嘗試最大化它們之間的距離。利用幾何學，我們發現這兩個超平面之間的距離是 ${\tfrac {2}{\|\mathbf {w} \|}}$，因此我們希望最小化 $\|\mathbf {w} \|$。由於我們還必須防止資料點落入間隔中，因此我們新增以下約束：對於每個 $i$ 都有

$\mathbf {w} \cdot \mathbf {x} _{i}-b\geq 1\qquad {\text{ for }}\mathbf {x} _{i}$ 屬於第一類

或

$\mathbf {w} \cdot \mathbf {x} _{i}-b\leq -1\qquad {\text{ for }}\mathbf {x} _{i}$ 屬於第二類。

這可以改寫為

$c_{i}(\mathbf {w} \cdot \mathbf {x} _{i}-b)\geq 1,\quad {\text{ for all }}1\leq i\leq n.\qquad \qquad (1)$

我們可以將這些組合起來得到最佳化問題

最小化（在 ${\mathbf {w} ,b}$ 中）

$\|\mathbf {w} \|$

受限於（對於任何 $i=1,\dots ,n$)

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.\,$

有偏超平面和無偏超平面

為了簡單起見，有時需要超平面透過座標系的原點。這種超平面被稱為無偏，而一般不一定要透過原點的超平面被稱為有偏。可以透過將 $b=0$ 設定為原始最佳化問題中的約束條件，強制執行無偏超平面。對應的對偶與上面給出的對偶相同，只是沒有等式約束條件

$\sum _{i=1}^{n}\alpha _{i}c_{i}=0.$

轉導支援向量機

轉導支援向量機擴充套件了 SVM，因為它也可以在半監督學習中處理部分標記資料。在這裡，除了訓練集 ${\mathcal {D}}$ 之外，學習器還會獲得一個集合

${\mathcal {D}}^{\star }=\{\mathbf {x} _{i}^{\star }|\mathbf {x} _{i}^{\star }\in \mathbb {R} ^{p}\}_{i=1}^{k}\,$

用於分類測試示例。形式上，轉導支援向量機由以下原始最佳化問題定義

最小化（在 ${\mathbf {w} ,b,\mathbf {c^{\star }} }$ 中）

${\frac {1}{2}}\|\mathbf {w} \|^{2}$

受限於（對於任何 $i=1,\dots ,n$ 和任何 $j=1,\dots ,k$)

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1,\,$

$c_{j}^{\star }(\mathbf {w} \cdot \mathbf {x_{j}^{\star }} -b)\geq 1,$

和

$c_{j}^{\star }\in \{-1,1\}.\,$

轉導支援向量機是由弗拉基米爾·瓦普尼克在1998年提出的。

特性

SVM屬於廣義線性分類器家族。它們也可以被認為是Tikhonov正則化的特例。一個特殊的屬性是，它們同時最小化經驗 *分類誤差* 並最大化 *幾何裕度*；因此它們也被稱為 *最大裕度分類器*。

邁耶、萊希和霍尼克對SVM與其他分類器的比較進行了研究。

線性SVM的擴充套件

軟間隔

1995年，科琳娜·科特斯和弗拉基米爾·瓦普尼克提出了一種修正後的最大間隔思想，允許存在錯誤標記的樣本。 如果不存在可以將“是”和“否”樣本分開的超平面，則 *軟間隔* 方法將選擇一個儘可能乾淨地劃分樣本的超平面，同時仍然最大化與最近的乾淨劃分樣本的距離。該方法引入了鬆弛變數，$\xi _{i}$，它們衡量資料點 $x_{i}$ 的錯誤分類程度。

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1-\xi _{i}\quad 1\leq i\leq n.\quad \quad (2)$

然後，目標函式透過一個懲罰非零 $\xi _{i}$ 的函式而增加，最佳化過程成為在較大裕度和較小誤差懲罰之間的權衡。如果懲罰函式是線性的，則最佳化問題變為

$\min _{\mathbf {w} ,\mathbf {\xi } }\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}\right\}$

受限於 (對於任何 $i=1,\dots n$)

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1-\xi _{i},~~~~\xi _{i}\geq 0.$

這種在 (2) 中的約束以及最小化 $\|\mathbf {w} \|$ 的目標可以使用拉格朗日乘子解決，如上所述。然後，需要解決以下問題：

$\min _{\mathbf {w} ,\mathbf {\xi } ,b}\max _{{\boldsymbol {\alpha }},{\boldsymbol {\beta }}}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}-\sum _{i=1}^{n}{\alpha _{i}[c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1+\xi _{i}]}-\sum _{i=1}^{n}\beta _{i}\xi _{i}\right\}$

其中 $\alpha _{i},\beta _{i}\geq 0$.

線性懲罰函式的主要優勢在於鬆弛變數從對偶問題中消失，常數 *C* 僅作為拉格朗日乘子的額外約束出現。對於上述公式及其在實踐中的巨大影響，Corinna Cortes|Cortes 和 Vladimir Vapnik|Vapnik 獲得了 2008 年巴黎卡內拉基斯獎|ACM 巴黎卡內拉基斯獎 。非線性懲罰函式已被使用，特別是在減少異常值對分類器影響方面，但除非謹慎處理，否則問題會變得非凸，因此找到全域性解決方案要困難得多。

非線性分類

弗拉基米爾·瓦普尼克在 1963 年提出的最初最佳超平面演算法是一種線性分類器。然而，在 1992 年，伯恩哈德·博瑟、伊莎貝爾·吉永和瓦普尼克提出了一種方法，透過將核技巧（最初由 Aizerman 等人提出） 應用於最大間隔超平面來建立非線性分類器。 結果演算法在形式上類似，只是每個點積都被非線性核（積分運算元）|核函式替換。這使得演算法能夠在轉換後的特徵空間中擬合最大間隔超平面。變換可能是非線性的，轉換後的空間可能是高維的；因此，儘管分類器在高維特徵空間中是超平面，但它在原始輸入空間中可能是非線性的。

如果使用的核是高斯徑向基函式，也稱為 RBF，則相應的特徵空間是無限維的希爾伯特空間。最大間隔分類器是良好正則化的，因此無限維不會破壞結果。一些常見的核心包括：

• 齊次多項式|多項式（齊次）： $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} )^{d}$
• 多項式（非齊次）： $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} +1)^{d}$
• 高斯或徑向基函式： $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\exp(-\gamma \|\mathbf {x_{i}} -\mathbf {x_{j}} \|^{2})$，對於 $\gamma >0$。有時使用 $\gamma =1/{2\sigma ^{2}}$ 引數化。
• 雙曲函式|雙曲正切：$k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\tanh(\kappa \mathbf {x_{i}} \cdot \mathbf {x_{j}} +c)$，對於某些（並非所有）$\kappa >0$ 和 $c<0$

核函式與變換 $\varphi (\mathbf {x_{i}} )$ 透過以下等式相關聯 $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\varphi (\mathbf {x_{i}} )\cdot \varphi (\mathbf {x_{j}} )$。w 的值也在變換空間中，其中 $\textstyle \mathbf {w} =\sum _{i}\alpha _{i}c_{i}\varphi (\mathbf {x} _{i}).$。用於分類的 w 的點積可以透過核技巧計算，即 $\textstyle \mathbf {w} \cdot \varphi (\mathbf {x} )=\sum _{i}\alpha _{i}c_{i}k(\mathbf {x} _{i},\mathbf {x} )$。然而，一般情況下不存在一個值 w' 使得 $\mathbf {w} \cdot \varphi (\mathbf {x} )=k(\mathbf {w'} ,\mathbf {x} ).$

引數選擇

SVM 的有效性取決於核函式、核函式的引數和軟間隔引數 C 的選擇。

一個常見的選擇是高斯核函式，它只有一個引數 ?。C 和 ? 的最佳組合通常透過網格搜尋選擇，網格搜尋使用指數增長的 C 和 ? 序列，例如，$C\in \{2^{-5},2^{-3},\dots ,2^{13},2^{15}\}$； $\gamma \in \{2^{-15},2^{-13},\dots ,2^{1},2^{3}\}$。每一對引數使用交叉驗證進行檢查，選擇具有最佳交叉驗證準確率的引數。最終模型用於測試和對新資料進行分類，它在整個訓練集上使用所選引數進行訓練。

問題

SVM 的潛在缺點如下兩個方面：

• 未校準的類成員機率
• SVM 僅直接適用於兩類任務。因此，必須應用將多類任務簡化為多個二元問題的演算法，參見多類 SVM 部分。

多類 SVM

多類別 SVM 旨在利用支援向量機為例項分配標籤，其中標籤來自一個包含多個元素的有限集合。最常用的方法是將單個多類別問題簡化為多個二元分類問題。每個問題都會產生一個二元分類器，該分類器被認為會產生一個輸出函式，該函式對來自正類的示例產生相對較大的值，而對來自負類的示例產生相對較小的值。構建此類二元分類器的兩種常用方法是：每個分類器區分（i）一個標籤與其餘標籤（一對多），或（ii）每個類別對之間（一對一）。對於一對多情況，新例項的分類透過贏家通吃策略完成，即輸出函式值最高的分類器分配類別（重要的是，輸出函式要經過校準以產生可比較的分數）。對於一對一方法，分類透過最大贏家投票策略完成，即每個分類器將例項分配到兩個類別之一，然後分配類別的投票增加一票，最後票數最多的類別決定例項的分類。

結構化 SVM

SVM 已被推廣到結構化 SVM，其中標籤空間是結構化的，並且可能具有無限大小。

迴歸

1996 年，弗拉基米爾·瓦普尼克、哈里斯·德魯克、克里斯·伯吉斯、琳達·考夫曼和亞歷克斯·斯莫拉提出了 SVM 用於迴歸分析|迴歸的一個版本。^[8] 這種方法被稱為支援向量迴歸 (SVR)。支援向量分類（如上所述）產生的模型僅取決於訓練資料的子集，因為構建模型的成本函式並不關心超出邊界的訓練點。類似地，SVR 產生的模型僅取決於訓練資料的子集，因為構建模型的成本函式會忽略任何靠近模型預測（在閾值 $\epsilon$ 內）的訓練資料。支援向量機 (SVM) 還存在一個最小二乘版本，稱為最小二乘支援向量機 (LS-SVM)，由 Suykens 和 Vandewalle 提出。^[9]

實現

最大邊距超平面的引數是透過求解最佳化問題得到的。存在幾種專門的演算法可以快速求解 SVM 產生的 QP 問題，這些演算法主要依賴於啟發式方法將問題分解為更小、更易於管理的塊。求解 QP 問題的常用方法是 Platt 的 序列最小最佳化 (SMO) 演算法，該演算法將問題分解為可以解析求解的二維子問題，從而無需數值最佳化演算法。

另一種方法是使用內點法，該方法使用牛頓迭代法來找到原始問題和對偶問題 Karush-Kuhn-Tucker 條件的解。^[10] 這種方法不是求解一系列分解問題，而是直接將問題作為一個整體求解。為了避免求解涉及大型核心矩陣的線性系統，通常會使用該矩陣的低秩近似來使用核心技巧。

SVM 平臺

目前存在多個數據科學平臺，提供 SVM 演算法的實現、訓練、驗證和測試。以下是一些例子

• Anaconda (Python 2.7, 3.5) (scikit learn)
• Matlab (統計和機器學習工具箱)

外部連結

• 支援向量機在模式識別中的教程 由 Christopher J. C. Burges 撰寫。資料探勘與知識發現 2:121–167, 1998
• www.kernel-machines.org (一般資訊和研究論文集)
• www.support-vector-machines.org (支援向量機相關文獻、綜述、軟體、連結 - 學術網站)
• videolectures.net (SVM 相關影片講座)
• 動畫剪輯: 使用多項式核的 SVM 視覺化。
• Tristan Fletcher 為完全初學者提供的非常基礎的 SVM 教程 [1].
• svmtutorial.online 對 SVM 的簡單介紹，任何具有基本數學背景的人都可以輕鬆理解
• www.shogun-toolbox.org (Shogun (工具箱) 包含大約 20 種不同的 SVM 實現)
• libsvm libsvm 是一個積極修補的 SVM 庫
• liblinear liblinear 是一個用於大型線性分類的庫，包括一些 SVM
• flssvm flssvm 是一個用 fortran 編寫的最小二乘 SVM 實現
• Shark Shark 是一個 C++ 機器學習庫，實現了各種型別的 SVM
• dlib dlib 是一個 C++ 庫，用於處理核方法和 SVM

參考文獻

• Sergios Theodoridis 和 Konstantinos Koutroumbas "模式識別", 第 4 版, Academic Press, 2009.
• Nello Cristianini 和 John Shawe-Taylor. 支援向量機和其他基於核的學習方法介紹. 劍橋大學出版社, 2000. ISBN 0-521-78019-5 ([2] SVM 書籍)
• Huang T.-M., Kecman V., Kopriva I. (2006), 用於挖掘海量資料集的基於核的演算法，監督、半監督和無監督學習，Springer-Verlag，柏林，海德堡，260 頁。96 幅插圖，精裝，ISBN 3-540-31681-7 [3]
• Vojislav Kecman: "學習與軟計算 - 支援向量機、神經網路、模糊邏輯系統", 麻省理工學院出版社，劍橋，馬薩諸塞州，2001.[4]
• Bernhard Schölkopf 和 A. J. Smola: 用核學習. 麻省理工學院出版社，劍橋，馬薩諸塞州，2002. (部分線上提供: [5].) ISBN 0-262-19475-9
• Bernhard Schölkopf, Christopher J.C. Burges 和 Alexander J. Smola (編輯)。"核方法進展: 支援向量學習". 麻省理工學院出版社，劍橋，馬薩諸塞州，1999. ISBN 0-262-19416-3. [6]
• John Shawe-Taylor 和 Nello Cristianini. 用於模式分析的核方法. 劍橋大學出版社，2004. ISBN 0-521-81397-2 ([7] 核方法書籍)
• Ingo Steinwart 和 Andreas Christmann. 支援向量機. Springer-Verlag，紐約，2008. ISBN 978-0-387-77241-7 ([8] SVM 書籍)
• P.J. Tan 和 D.L. Dowe (2004), 斜決策樹的 MML 推斷, 人工智慧講義 (LNAI) 3339, Springer-Verlag, pp1082-1088. (本文使用最小訊息長度 (最小訊息長度|MML) 並且實際上將機率支援向量機整合到決策樹學習|決策樹的葉子中)。
• Vladimir Vapnik. 統計學習理論的本質. Springer-Verlag, 1995. ISBN 0-387-98780-0
• Vladimir Vapnik, S.Kotz "基於經驗資料的依賴估計" Springer, 2006. ISBN 0387308652, 510 頁 [這是 Vapnik 早期書籍的轉載，描述了 SVM 方法背後的理念。2006 年的附錄描述了最近的發展]。
• Dmitriy Fradkin 和 Ilya Muchnik "用於分類的支援向量機" 在 J. Abello 和 G. Carmode (編) "流行病學中的離散方法" 中，DIMACS 離散數學與理論計算機科學叢書，第 70 卷，第 13-20 頁，2006. [9]. 簡潔地描述了 SVM 背後的理論思想。
• Kristin P. Bennett 和 Colin Campbell, "支援向量機: 炒作還是讚歌?", SIGKDD 探索, 2,2, 2000, 1-13. [10]. 對 SVM 的出色介紹，包含有用的圖表。
• Ovidiu Ivanciuc, "支援向量機在化學中的應用", 在: 計算化學評論, 第 23 卷, 2007, 第 291-400 頁. 可轉載: [11]
• Catanzaro, Sundaram, Keutzer, "圖形處理器上的快速支援向量機訓練和分類", 在: 國際機器學習大會, 2008 [12]