量子世界/附錄/微積分

微積分：一個非常簡短的介紹

另一種方法，我們可以從無窮小的量中獲得一個定義明確的有限數，就是將一個這樣的量除以另一個量。

我們將在整個過程中假設我們正在處理行為良好的函式，這意味著你可以繪製這樣的函式的圖形而不抬起你的鉛筆，並且你也可以對函式的每個導數做同樣的事情。那麼什麼是函式，什麼是函式的導數呢？

一個函式 $f(x)$ 是一個帶有輸入和輸出的機器。輸入一個數字 $x$ ，就會輸出數字 $f(x).$ 有點令人困惑的是，我們有時將 $f(x)$ 不僅僅看作一個輸出數字的機器，而是看作當插入 $x$ 時輸出的數字。

（第一個）導數 $f'(x)$ 的 $f(x)$ 是一個函式，它告訴我們 $f(x)$ 在 $x$ 增加時（從給定值開始 $x,$ 比如 $x_{0}$ ) 增加多少，在 $x$ 的增加量 $\Delta x$ 和 $f(x)$ 的對應增加量 $\Delta f=f(x+\Delta x)-f(x)$ （當然可能為負）趨於 0

f'(x_{0})=\lim _{\Delta x\rightarrow 0}{\Delta f \over \Delta x}={df \over dx}(x_{0}).

上面的圖表說明了這個極限。比值 $\Delta f/\Delta x$ 是穿過黑點的直線的斜率（即 $\tan$ 正 $x$ 軸與直線之間的夾角，從正 $x$ 軸逆時針方向測量）。當 $\Delta x$ 減小，位於 $x+\Delta x$ 的黑點沿著 $f(x)$ 的圖形滑向位於 $x,$ 的黑點，而直線的斜率增大。在極限 $\Delta x\rightarrow 0,$ 時，直線成為 $f(x),$ 的切線，在 $x.$ 與其相切。 $f(x)$ 在 $x_{0}$ 處的切線的斜率就是我們所說的 $f(x)$ 在 $x_{0}.$

所以，函式 $f(x)$ 的一階導數 $f'(x)$ 是一個函式，它對於每個 $x.$ 都等於 $f(x)$ 的斜率。求導一個函式 $f$ 就是求得它的一階導數 $f'.$ 對 $f',$ 求導，我們得到 $f,$ 的二階導數 $f''={\frac {d^{2}f}{dx^{2}}}$ ，對 $f''$ 求導，我們得到三階導數 $f'''={\frac {d^{3}f}{dx^{3}}},$ 等等。

很容易證明，如果 $a$ 是一個數字，並且 $f$ 和 $g$ 是 $x,$ 的函式，則

{d(af) \over dx}=a{df \over dx}

和

{d(f+g) \over dx}={df \over dx}+{dg \over dx}.

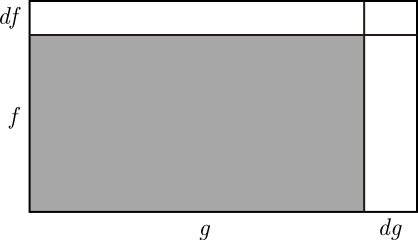
一個稍微難一點的問題是，求兩個關於 $x.$ 的函式的乘積 $e=fg$ 的導數。將 $f$ 和 $g$ 視為面積為 $e.$ 的矩形的垂直邊和水平邊。當 $x$ 增加 $\Delta x,$ 乘積 $fg$ 增加圖中三個白色矩形的面積之和。

換句話說，

\Delta e=f(\Delta g)+(\Delta f)g+(\Delta f)(\Delta g)

因此

{\frac {\Delta e}{\Delta x}}=f\,{\frac {\Delta g}{\Delta x}}+{\frac {\Delta f}{\Delta x}}\,g+{\frac {\Delta f\,\Delta g}{\Delta x}}.

如果我們現在取極限，其中 $\Delta x$ 以及因此 $\Delta f$ 和 $\Delta g$ 趨近於 0，則右手邊的前兩項趨近於 $fg'+f'g.$ 第三項怎麼樣？因為它是一個趨近於 0 的表示式（ $\Delta f$ 或 $\Delta g$ ）與一個趨近於有限值的表示式（ $\Delta g/\Delta x$ 或 $\Delta f/\Delta x$ ）的乘積，因此它趨近於 0。底線

e'=(fg)'=fg'+f'g.

這很容易推廣到 $n$ 個函式的乘積。這是一個特例

(f^{n})'=f^{n-1}\,f'+f^{n-2}\,f'\,f+f^{n-3}\,f'\,f^{2}+\cdots +f'\,f^{n-1}=n\,f^{n-1}f'.

觀察到，兩個等號之間有 $n$ 個相等的項。如果函式 $f$ 返回你插入的任何東西，這歸結為

(x^{n})'=n\,x^{n-1}.

現在假設 $g$ 是 $f$ 的函式，而 $f$ 是 $x.$ 的函式。當 $x$ 增加 $\Delta x$ 時， $f$ 增加 $\Delta f\approx {\frac {df}{dx}}\Delta x,$ 這反過來會導致 $g$ 增加 $\Delta g\approx {\frac {dg}{df}}\Delta f.$ 因此 ${\frac {\Delta g}{\Delta x}}\approx {\frac {dg}{df}}{\frac {df}{dx}}.$ 在極限 $\Delta x\rightarrow 0$ 時， $\approx$ 變為 $=$