想象一個物體 ,它可以自由地在單一維度運動 - 例如,沿著
,它可以自由地在單一維度運動 - 例如,沿著 軸。就像任何物理物體一樣,它具有或多或少的模糊位置(相對於我們選擇的任何參考物體)。為了描述它的模糊位置,量子力學為我們提供了機率密度
軸。就像任何物理物體一樣,它具有或多或少的模糊位置(相對於我們選擇的任何參考物體)。為了描述它的模糊位置,量子力學為我們提供了機率密度  這取決於實際的測量結果,它允許我們計算在
這取決於實際的測量結果,它允許我們計算在 軸的任何給定區間內找到粒子的機率,前提是進行了適當的測量。(記住我們的口號:量子力學的數學形式主義是為了根據實際結果為可能的測量結果分配機率。)
軸的任何給定區間內找到粒子的機率,前提是進行了適當的測量。(記住我們的口號:量子力學的數學形式主義是為了根據實際結果為可能的測量結果分配機率。)
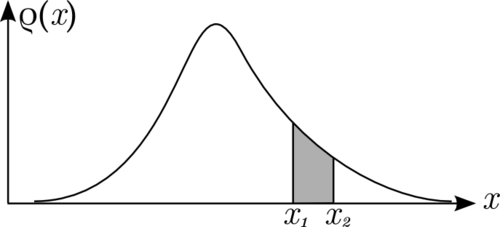
我們稱 為機率密度,因為它表示每單位長度的機率。在
為機率密度,因為它表示每單位長度的機率。在 和
和  之間的區間內找到
之間的區間內找到 的機率由
的機率由 的圖形、
的圖形、 軸以及在
軸以及在 和
和  處的垂直線之間的面積
處的垂直線之間的面積  所給出。我們如何計算這個面積?訣竅是用寬度為
所給出。我們如何計算這個面積?訣竅是用寬度為 的窄矩形覆蓋它。
的窄矩形覆蓋它。

左側第一個矩形的面積為  ,第二個矩形的面積為
,第二個矩形的面積為  ,最後一個矩形的面積為
,最後一個矩形的面積為  這些面積的總和可以用簡寫符號表示為
這些面積的總和可以用簡寫符號表示為

不難想象,如果我們增加矩形數量  ,同時減小每個矩形的寬度
,同時減小每個矩形的寬度  ,那麼所有這些矩形的面積總和,都將越來越逼近
,那麼所有這些矩形的面積總和,都將越來越逼近  在
在  和
和  之間曲線下的面積
之間曲線下的面積  ,從而越來越逼近找到
,從而越來越逼近找到  在
在  和
和  當
當  趨於 0 且
趨於 0 且  趨於無窮大 (
趨於無窮大 ( ) 時,上面的求和式將趨於積分
) 時,上面的求和式將趨於積分

有時我們將此稱為定積分,以強調它只是一個數字。(正如你所料,也有不定積分,你將在後面學習更多關於它們的內容。)大寫 Δ 已變成一個  ,表明
,表明  是一個無限小的(或無窮小)寬度,求和符號(大寫 Σ)已變成一個拉長的 S,表示我們正在新增無限多個無窮小面積。
是一個無限小的(或無窮小)寬度,求和符號(大寫 Σ)已變成一個拉長的 S,表示我們正在新增無限多個無窮小面積。
不要讓“無窮小”這個詞嚇到你。一個無窮小量本身沒有意義。它是組合了積分符號  和無窮小量
和無窮小量  ,它作為極限是有意義的,其中
,它作為極限是有意義的,其中  超過任何大數字,
超過任何大數字, (因此每個矩形的面積)縮小到任何(正)數字以下,無論它多麼小,而面積之和趨向於一個明確定義的有限數字。
(因此每個矩形的面積)縮小到任何(正)數字以下,無論它多麼小,而面積之和趨向於一個明確定義的有限數字。
























