量子世界/附錄/相對論/洛倫茲

反對 $K>0$ 的論據

在一個假設的 $K>0$ 的世界中，我們可以定義 $k\equiv 1/{\sqrt {K}}$ （一個具有速度維度的通用常數），我們可以將 $u=v+w/(1-Kvw)$ 轉換為以下形式

$u={v+w \over 1-vw/k^{2}}.$

If we plug in $v=w=k/2,$ then instead of the Galilean $u=v+w=k$ we have $u={4 \over 3}k>k.$ Worse, if we plug in $v=w=k,$ we obtain $u=\infty$: if object $O$ travels with speed $k$ relative to ${\mathcal {F}}_{2},$ and if ${\mathcal {F}}_{2}$ travels with speed $k$ relative to ${\mathcal {F}}_{1}$ (in the same direction), then $O$ travels with an infinite speed relative to ${\mathcal {F}}_{1}$! And if $O$ travels with $2k$ relative to ${\mathcal {F}}_{2}$ and ${\mathcal {F}}_{2}$ travels with $2k$ relative to ${\mathcal {F}}_{1},$ $O$'s speed relative to ${\mathcal {F}}_{1}$ is negative: $u=-{4 \over 3}k.$

如果我們使用單位 $K=k=1,$，則與無限小路徑段相關的固有時間與該路徑段的慣性分量之間的關係為

$ds^{2}=dt^{2}+dx^{2}+dy^{2}+dz^{2}.$

這是 3 標量 $dx^{2}+dy^{2}+dz^{2},$ 的 4 維版本，它在空間旋轉下是不變的。因此，如果 $K$ 為正，則慣性系統之間的變換是時空中的旋轉。我想你現在明白為什麼在這個假設的世界中，兩個正速度的合成可以是負速度。

讓我們透過從假設 $x'$ 和 $t'$ 軸相對於 $x$ 和 $t$ 軸旋轉來推匯出合成定理（對於 $k{=}1$）

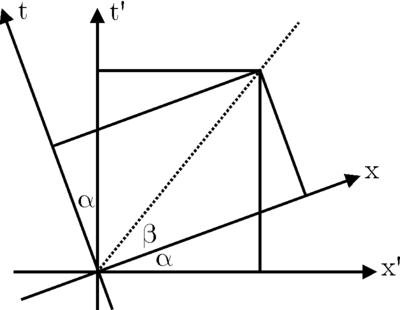
沿著虛線運動的物體 $O$ 相對於 ${\mathcal {F}}',$ 的速度為 $w=\cot(\alpha +ta)$， ${\mathcal {F}}'$ 相對於 ${\mathcal {F}}$ 的速度為 $v=\tan \alpha ,$，而 $O$ 相對於 ${\mathcal {F}}$ 的速度為 $u=\cot \beta .$ 利用三角關係

$\tan(\alpha +\beta )={\tan \alpha +\tan \beta \over 1-\tan \alpha \tan \beta },$

我們可以得出結論 ${1 \over w}={v+1/u \over 1-v/u}.$ 求解 $u,$ 我們得到 $u={v+w \over 1-vw}.$

我們如何排除 $K>0$ 這一先驗可能性？正如本書正文所述，物質的穩定性——更準確地說，存在穩定的物體（i）具有空間範圍（它們“佔據”空間），並且（ii）由有限數量的物體組成，這些物體沒有空間範圍（它們不“佔據”空間）——取決於存在（a）或多或少模糊的相對位置和（b）與時間無關的相對位置。這些相對位置由機率分佈描述，這些分佈（a）在空間上不均勻並且（b）在時間上均勻。因此，它們的客觀存在需要時空的時間維度與其空間維度之間的客觀差異。這排除了 $K>0.$ 的可能性。

為什麼？如果 $K<0,$ 並且如果我們使用自然單位，其中 $c=1,$ 我們有

$ds^{2}=+\,dt^{2}-dx^{2}-dy^{2}-dz^{2}.$

從物理學的角度來看，$dt$ 前面的正號和$dx,$ $dy,$ 和 $dz$ 前面的負號之間的唯一客觀區別是時空的時間維和空間維。如果 $K$ 為正，即使是這種差異也不存在。

反對 K 為零的情況

那麼，什麼能反駁 $K=0$ 的可能性呢？

回顧一下自由穩定粒子的傳播子

$\langle B|A\rangle =\int {\mathcal {DC}}e^{-ibs[{\mathcal {C}}]}.$

如果 $K$ 消失，我們會有 $ds^{2}=dt^{2}.$ 慣性時間和固有時之間沒有區別，從 $A$ 到 $B$ 的每條時空路徑都會對傳播子 $\langle B|A\rangle ,$ 貢獻相同的振幅 $e^{-ib(t_{B}-t_{A})}$，這會導致傳播子 $\langle B|A\rangle$ 毫無希望地發散。更糟糕的是，$\langle B|A\rangle$ 將獨立於 $A$ 和 $B.$ 之間的距離。為了獲得定義明確的有限機率，必須發生抵消（“相消干涉”），這排除了 $K=0.$

實際的洛倫茲變換

因此，在現實世界中，洛倫茲變換採用以下形式

$t'={t-wx/c^{2} \over {\sqrt {1-w^{2}/c^{2}}}},\quad x'={x-wt \over {\sqrt {1-w^{2}/c^{2}}}},\quad y'=y,\quad z'=z.$

讓我們使用自然單位（$c=1$）以圖形方式探索它們。設定 $t'=0,$ 我們有 $t=wx.$ 這告訴我們，$x'$ 軸相對於未標軸的框架的斜率為 $w=\tan \alpha .$ 設定 $x'=0,$ 我們有 $t=x/w.$ 這告訴我們，$t'$ 軸的斜率為 $1/w.$ 因此，標軸以相同的角度在相反的方向旋轉；如果 $t'$ 軸相對於 $t$ 軸順時針旋轉，那麼 $x'$ 軸相對於 $x$ 軸逆時針旋轉。

如果我們考慮運動中時鐘的同步，我們會得出相同的結論。考慮三個時鐘（1,2,3），它們以相同的速度$w=\tan \alpha$相對於 ${\mathcal {F}}.$ 為了同步它們，我們必須從一個時鐘向另一個時鐘傳送訊號。什麼樣的訊號？如果我們希望我們的同步過程獨立於我們使用的語言（即獨立於參考系），那麼我們必須使用以不變速度傳播的訊號 $c.$

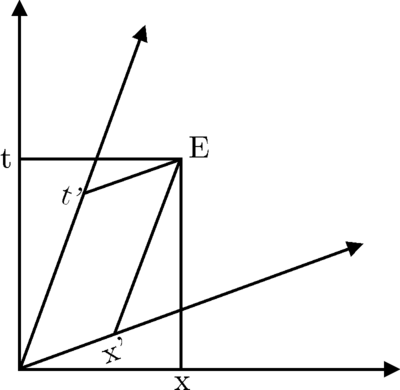
以下是具體操作方法

時鐘 2 傳送光訊號（事件 $A$），並被時鐘 1 和 3 反射（事件 $B$ 和 $C,$ 分別）。時鐘之間的距離被調整，以便反射的訊號同時到達時鐘 2（事件 $D$）。這確保了時鐘 1 和 2 之間的距離等於時鐘 2 和 3 之間的距離，無論比較它們使用的慣性系如何。在 ${\mathcal {F}}',$ 中，時鐘處於靜止狀態，來自 $A$ 的訊號在分別到達第一個和第三個時鐘時，已經傳播了相同的距離。由於它們也以相同的速度 $c,$ 傳播，因此它們傳播的時間相同。因此，時鐘必須同步，以便 $B$ 和 $C$ 是同時發生的。我們可以使用時鐘 1 的世界線作為 $t'$ 軸，並將穿過 $B$ 和 $C$ 的直線作為 $x'$ 軸。可以很容易地看出，上圖中的三個角度 $ta$ 是相等的。由此以及從 $B$ 到 $D$ 的訊號的斜率等於 1（鑑於 $c{=}1$），可以得出兩個角度 $\alpha$ 相等的結論。

因此，同時性取決於我們用來描述物理情況的語言——慣性系。如果兩個事件$E_{1},E_{2}$在一個參考系中是同時發生的，那麼就存在其他參考系，在這些參考系中$E_{1}$發生在$E_{2}$之後，以及存在其他參考系，在這些參考系中$E_{1}$發生在$E_{2}.$

我們在空間和時間軸上放置單位點在哪裡？${\mathcal {F}}'$的時間軸的單位點具有座標$t'=1,x'=0$，並且滿足$t^{2}-x^{2}=1,$正如我們從公式（\ref{ds2}）的版本$(t')^{2}-(x')^{2}=t^{2}-x^{2}$中獲得的。$x'$軸的單位點具有座標$t'=0,x'=1$，並且滿足$x^{2}-t^{2}=1.$空間和時間軸的單位點的軌跡是由這些方程定義的雙曲線。