量子世界/附錄/相對論/洛倫茲收縮時間膨脹

洛倫茲收縮，時間膨脹

想象一根靜止在 ${\mathcal {F}}'.$ 中的米尺。在時間 $t'=0,$，它的兩端位於點 $O$ 和 $C.$ 在時間 $t=0,$ 它們位於點 $O$ 和 $A,$ 這兩點之間的距離小於一米。現在想象一根靜止在 ${\mathcal {F}},$ 中的棍子（不是米尺），它的兩端在時間 $t'=0$ 位於 O 和 C。在 ${\mathcal {F}}'$ 中它們之間距離一米，但在棍子的靜止系中它們位於點 $O$ 和 $B$，因此距離超過一米。底線：運動物體在運動方向上會收縮（縮短）。

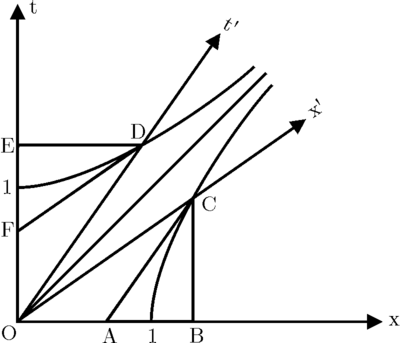
接下來想象兩個時鐘，一個 (${\mathcal {C}}$) 在 ${\mathcal {F}}$ 中靜止，位於 $x=0,$ 另一個 (${\mathcal {C}}'$) 在 ${\mathcal {F}}'$ 中靜止，位於 $x'=0.$ 在 $D,$ ${\mathcal {C}}'$ 表明已經過去了1秒，而在 $E$（在 ${\mathcal {F}}$ 中與 $D$ 同時發生），${\mathcal {C}}$ 表明已經過去了超過1秒。另一方面，在 $F$（在 ${\mathcal {F}}'$ 中與 $D$ 同時發生），${\mathcal {C}}$ 表明已經過去了不到1秒。結論是：運動的時鐘比靜止的時鐘走得慢。

例如：μ子 ($\mu$ 粒子) 在大氣層頂部附近產生，大約在10公里處，當來自宇宙的高能粒子撞擊大氣層時。由於μ子自發衰變，平均壽命為2.2微秒，因此它們的行進距離不超過600米。然而，許多μ子被發現到達海平面。它們是如何到達那裡的呢？

答案在於，大多數μ子以接近光速的速度運動。從μ子自身的角度來看（即相對於它處於靜止狀態的慣性系），μ子的壽命只有大約2微秒；但從我們的角度來看（即相對於一個慣性系，其中μ子以接近光速的速度運動），μ子的壽命要長得多，有足夠的時間到達地球表面。