量子世界/附錄/向量

向量（空間）

一個 向量 是既有大小又有方向的量。向量可以被視覺化為箭頭。下圖展示了我們對向量 $\mathbf {a} .$ 的分量 $(a_{x},a_{y},a_{z})$ 的理解。

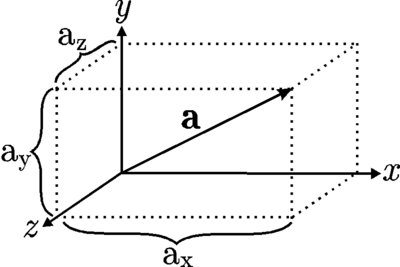
兩個向量的和 $\mathbf {a} +\mathbf {b}$ 的分量為 $(a_{x}+b_{x},a_{y}+b_{y},a_{z}+b_{z}).$

• 用箭頭解釋向量的加法。

兩個向量的 點積 是一個數

$\mathbf {a} \cdot \mathbf {b} =a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}.$

它的重要性在於它在 旋轉 下是不變的。為了證明這一點，我們計算

$(\mathbf {a} +\mathbf {b} )\cdot (\mathbf {a} +\mathbf {b} )=(a_{x}+b_{x})^{2}+(a_{y}+b_{y})^{2}+(a_{z}+b_{z})^{2}=$

$a_{x}^{2}+a_{y}^{2}+a_{z}^{2}+b_{x}^{2}+b_{y}^{2}+b_{z}^{2}+2\,(a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z})=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} +2\,\mathbf {a} \cdot \mathbf {b} .$

根據畢達哥拉斯定理，$\mathbf {a}$ 的大小為 $a={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}.$ 如果我們使用不同的座標系，$\mathbf {a}$ 的分量將不同：$(a_{x},a_{y},a_{z})\rightarrow (a'_{x},a'_{y},a'_{z}).$ 但是如果新的座標系僅僅是透過旋轉和/或平移得到的，$\mathbf {a}$ 的大小將保持不變

${\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}={\sqrt {(a'_{x})^{2}+(a'_{y})^{2}+(a'_{z})^{2}}}.$

平方的大小 $\mathbf {a} \cdot \mathbf {a} ,$ $\mathbf {b} \cdot \mathbf {b} ,$ 和 $(\mathbf {a} +\mathbf {b} )\cdot (\mathbf {a} +\mathbf {b} )$ 在旋轉下是不變的，因此，乘積 $\mathbf {a} \cdot \mathbf {b} .$

• 證明點積在平移下也是不變的。

由於標量是指在某些變換下（在本例中為座標軸的旋轉和/或平移）保持不變的數字，因此點積也被稱為（a）標量積。我們來證明

$\mathbf {a} \cdot \mathbf {b} =ab\cos \theta ,$

其中 $\theta$ 是 $\mathbf {a}$ 和 $\mathbf {b} .$ 之間的夾角。為此，我們選擇一個座標系 ${\mathcal {F}}$，其中 $\mathbf {a} =(a,0,0).$ 在此座標系中，$\mathbf {a} \cdot \mathbf {b} =ab_{x}$，其中 $b_{x}=b\cos \theta .$ 由於 $\mathbf {a} \cdot \mathbf {b}$ 是一個標量，並且標量在旋轉和平移下是不變的，所以結果 $\mathbf {a} \cdot \mathbf {b} =ab\cos \theta$（不依賴於任何特定框架）在相對於 ${\mathcal {F}}.$ 旋轉和平移的所有框架中都成立。

現在我們引入單位向量 $\mathbf {\hat {x}} ,\mathbf {\hat {y}} ,\mathbf {\hat {z}} ,$，它們的指向由座標軸定義。它們被稱為構成一個正交規範基。正交是因為它們彼此正交

$\mathbf {\hat {x}} \cdot \mathbf {\hat {y}} =\mathbf {\hat {x}} \cdot \mathbf {\hat {z}} =\mathbf {\hat {y}} \cdot \mathbf {\hat {z}} =0.$

規範是因為它們是單位向量

$\mathbf {\hat {x}} \cdot \mathbf {\hat {x}} =\mathbf {\hat {y}} \cdot \mathbf {\hat {y}} =\mathbf {\hat {z}} \cdot \mathbf {\hat {z}} =1.$

它們是“**正交的**”，因為它們是相互垂直的；它們也是“**標準化的**”，因為它們的大小都是 1。 而它們被稱作“**基**”是因為每一個向量 $\mathbf {v}$ 都可以被寫成這三個向量的 線性組合 —— 也就是說，一個每個基向量出現一次的求和，並乘以 $\mathbf {v}$ 的對應分量（該分量可以是 0）

$\mathbf {v} =v_{x}\mathbf {\hat {x}} +v_{y}\mathbf {\hat {y}} +v_{z}\mathbf {\hat {z}} .$

可以很容易地看出 $v_{x}=\mathbf {\hat {x}} \cdot \mathbf {v} ,$ $v_{y}=\mathbf {\hat {y}} \cdot \mathbf {v} ,$ $v_{z}=\mathbf {\hat {z}} \cdot \mathbf {v} ,$ 這就是我們有以下結論的原因

$\mathbf {v} =\mathbf {\hat {x}} \,(\mathbf {\hat {x}} \cdot \mathbf {v} )+\mathbf {\hat {y}} \,(\mathbf {\hat {y}} \cdot \mathbf {v} )+\mathbf {\hat {z}} \,(\mathbf {\hat {z}} \cdot \mathbf {v} ).$

另一個有用的定義（儘管只適用於 3 維空間）是兩個向量的 叉積

$\mathbf {a} \times \mathbf {b} =(a_{y}b_{z}-a_{z}b_{y})\,\mathbf {\hat {x}} +(a_{z}b_{x}-a_{x}b_{z})\,\mathbf {\hat {y}} +(a_{x}b_{y}-a_{y}b_{x})\,\mathbf {\hat {z}} .$

• 證明叉積是反對稱的：$\mathbf {a} \times \mathbf {b} =-\mathbf {b} \times \mathbf {a} .$

因此，$\mathbf {a} \times \mathbf {a} =0.$

• 證明$\mathbf {a} \cdot (\mathbf {a} \times \mathbf {b} )=\mathbf {b} \cdot (\mathbf {a} \times \mathbf {b} )=0.$

因此$\mathbf {a} \times \mathbf {b}$ 與$\mathbf {a}$ 和 $\mathbf {b} .$ 垂直。

• 證明$\mathbf {a} \times \mathbf {b}$ 的大小等於 $ab\sin \alpha ,$ 其中 $\alpha$ 是$\mathbf {a}$ 和 $\mathbf {b} .$ 之間的夾角。提示：使用一個座標系，其中 $\mathbf {a} =(a,0,0)$ 且 $\mathbf {b} =(b\cos \alpha ,b\sin \alpha ,0).$

因為 $ab\sin \alpha$ 也是平行四邊形 $P$ 的面積 $A$，我們可以將 $\mathbf {a} \times \mathbf {b}$ 看作一個大小為 $A$ 的向量，它垂直於 $P.$ 由於叉積產生一個向量，它也被稱為向量積。

（我們省去了證明叉積在座標軸平移和旋轉下是不變的，這是向量所必需的。但是，讓我們順便提一下，如果 $\mathbf {a}$ 和 $\mathbf {b}$ 是極向量，那麼 $\mathbf {a} \times \mathbf {b}$ 是一個軸向量。在反射（例如，座標軸的反轉）下，一個普通（或極性）向量是不變的，而一個軸向量改變了它的符號。）

這裡有一個涉及標量積和向量積的實用關係

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} .$