原子

原子看起來像什麼？

像這樣？

還是像這樣？

$\rho _{2p0}$
$\rho _{3p0}$
$\rho _{3d0}$
$\rho _{4p0}$
$\rho _{4d0}$
$\rho _{4f0}$
$\rho _{5d0}$
$\rho _{5f0}$

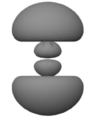
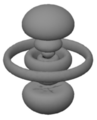
這些影像都沒有描述真實的原子。這是因為我們甚至無法真實地視覺化原子。雖然你可以嘗試將第一行中的影像從你的記憶中抹去——它們代表了一種看待原子的方式，這種方式過於簡化，不適合我們想要開始思考的方式——但下一行中的八個模糊影像值得仔細研究。每個影像都代表了氫原子的靜止態的一個方面。你既無法感知原子核（一個質子），也無法感知電子。你所看到的是一個模糊的位置。更準確地說，你所看到的是雲狀的模糊，它們關於垂直和水平軸對稱，並且代表了原子的內部相對位置——電子相對於質子的位置或質子相對於電子的位置。

原子的狀態是什麼？
什麼是靜止態？
模糊的位置到底是什麼？
這種模糊是如何代表原子的內部相對位置的？
為什麼我們不能真實地描述原子的內部相對位置？

量子態

在量子力學中，態是機率演算法。我們使用它們根據實際測量結果來計算對測量的可能結果的機率。量子態將其輸入作為

一個或多個測量結果，
一個測量 M，
M 的時間，

它將其輸出作為 M 的可能結果的機率。

如果量子態所分配的機率獨立於測量時間，則稱其為靜止態。

從數學的角度來看，每個模糊圖代表一個密度函式 $\rho ({\boldsymbol {r}})$ 。想象一個小的區域 $R$ ，就像第一個模糊圖中的小方塊。假設這是一個相對於質子的位置（數學）空間的區域。如果你在 $R$ 上對 $\rho ({\boldsymbol {r}})$ 進行積分，你將得到找到電子在 $R$ 中的機率 $p\,(R)$ ，前提是進行了適當的測量。

p\,(R)=\int _{R}\rho ({\boldsymbol {r}})\,d^{3}{\boldsymbol {r}}.

這裡“適當”是指能夠確定命題“電子在 $R$ 中”的真值，可能的真值為“真”或“假”。我們在以下每個影像中看到的是一個恆定機率密度的表面。

$\rho _{2p0}$
$\rho _{3p0}$
$\rho _{3d0}$
$\rho _{4p0}$
$\rho _{4d0}$
$\rho _{4f0}$
$\rho _{5d0}$
$\rho _{5f0}$

現在想象一下進行了適當的測量。在測量之前，電子既不在 $R$ 內也不在 $R$ 外。如果它在裡面，那麼在外面找到它的機率為零；如果它在外面，那麼在裡面找到它的機率為零。在測量之後，另一方面，電子要麼在 $R$ 內，要麼在 $R$ 外。

結論

在測量之前，命題“電子在 $R$ 中”既不是真也不是假；它缺乏一個（確定的）真值。
測量通常會改變其作用的系統的狀態。

如前所述，機率不僅分配給測量結果，而且基於測量結果。每個密度函式 $\rho _{nlm}$ 用於為測量電子相對於質子的位置的可能結果分配機率。在每種情況下，分配都基於對三個可觀察量的同時測量的結果：原子的能量（由主量子數 $n$ 的值指定），其總角動量 $l$ （由一個字母指定，這裡為p、d或f），以及其角動量的垂直分量 $m$ 。

模糊的可觀察量

我們說一個可觀察量 $Q$ 具有有限或可數的可能值 $q_{k}$ 是模糊的（或者說它具有模糊值）當且僅當至少有一個命題“ $Q$ 的值為 $q_{k}$ ” 缺乏真值。這等效於以下充要條件：分配給至少一個值 $q_{k}$ 的機率既不是 0 也不是 1。

那麼對於通常被描述為連續的可觀察量，比如位置，情況又如何呢？

將一個可觀察量描述為“連續”可能具有誤導性。一方面，我們不能將一個可觀察量及其可能值與測量及其可能結果分離，而具有不可數個可能結果的測量在原則上也是不可能的。另一方面，不存在一個名為“位置”的單一可觀察量。空間的不同劃分定義了具有不同可能結果集的不同位置測量。

推論：位置測量的可能結果（或位置可觀察量的可能值）由空間的劃分定義。它們構成一個有限或可數的空間區域集合。因此，精確的位置既不是可能的測量結果，也不是位置可觀察量的可能值。

那麼這些雲狀模糊如何表示電子相對於質子的模糊位置呢？嚴格地說，它們以圖形方式表示精確相對位置的數學空間中的機率密度，而不是模糊位置。正是這些機率密度透過允許我們計算每個位置可觀察量的每個可能值的機率來表示模糊位置。

現在應該清楚為什麼我們不能描述原子的內部相對位置本身。描述一個模糊的可觀察量就是給測量可能的結果分配機率。但是，一個基於測量已完成的假設的描述，並沒有描述一個可觀察量本身（本身，無論測量與否）。

NEXT >