運輸地理與網路科學/彈性
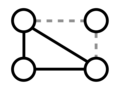
Sudakov 和 Vu (2008)[1]提出了圖論中彈性的最具體定義:如果圖 G 具有屬性 P,那麼需要移除多少條邊才能使 G 不再具有 P?[2]例如,考慮圖 1 及其關於連通性的彈性。移除任何一條邊都會留下一個仍然連通的圖。必須移除兩條邊才能生成一個不連通的圖(圖 2)。因此,我們可以說這個圖關於連通性具有 2 的彈性。請注意,這並不意味著移除任何兩條邊都會破壞這個圖的連通性。圖 3 展示了在移除兩條邊後仍然保持圖連通的可能性。
-
圖 1
-
圖 2
-
圖 3
根據這個定義,給定圖在不同屬性方面將具有不同的彈性值。因此,該定義是具體的,但靈活的,可以有效地應用於現實世界的網路,其中屬性從不同角度來看具有不同的重要性。
一些關於彈性的討論側重於頂點移除而不是邊移除。移除一個頂點對網路其餘部分的影響等同於移除連線到該頂點的所有邊的影響。
上面的例子突出了隨機邊移除和目標邊移除之間的區別。如果隨機移除邊,屬性可能會在移除許多邊後仍然存在。目標邊移除意味著分析圖並選擇能夠達到最小值的邊。[3]
兩種型別的邊移除對網路的影響部分取決於度分佈。遵循冪律分佈(無標度)的圖往往對隨機邊移除具有很強的彈性,因為移除的邊很有可能只連線低度頂點,因此整體圖結構只會受到輕微影響。然而,它們對連線到高度頂點的邊的目標移除,特別是對這些頂點本身的移除,要脆弱得多。在無標度圖中,這些高度頂點在連線子圖方面至關重要。[3]
一個在某個屬性方面彈性低的圖,可能會因為僅僅移除幾條邊而失去該屬性。我們可以說該圖在該屬性方面很脆弱。
但這僅僅是對脆弱性完整考慮的一部分。另一半則要考慮如果該屬性丟失對網路效能的影響,這在運輸地理與網路科學/可靠性中討論。

在圖論中,彈性是一個二元概念:一條邊要麼存在,要麼不存在;一個圖要麼具有某個屬性,要麼不具有。在現實世界的交通網路中,鏈路具有額外的屬性,例如容量和成本。我們可以透過考慮鏈路屬性變化對整體網路屬性的影響,將彈性的概念應用於交通網路。

例如,考慮圖 4 中的網路,其中節點表示城市,鏈路表示貨運鐵路。每條鏈路都有一個成本,表示穿越它的所需時間(以小時為單位)。網路的一個屬性是存在一條從 A 到 D 的路徑,其總成本為 10 小時或更少。現在想象一下,發生了一些事件,導致 A-D 鏈路的成本增加了 50%,達到 15。事件的具體性質無關緊要;它可能是暴風雪、疲勞的鐵軌或政府實施的限速。這個事件足以破壞網路具有從 A 到 D 的 10 小時或更少成本路徑的屬性。
然而,它並沒有破壞網路的連通性屬性;A 和 D 仍然是連通的(儘管路徑成本更高)。在評估交通網路的彈性時,重要的是要記住,網路在不同屬性方面將具有不同的彈性水平。
一旦評估了網路在某個屬性方面的彈性,通常希望提高彈性。這可以透過兩種基本方法來實現:新增冗餘或過度配置現有鏈路。(Bell 2000,前言)
想象一下,我們可以將鏈路 A-B 和 C-D 的成本從 8 降低到 6,如圖 5 所示。這個改進後的網路具有三條從 A 到 D 的節點獨立路徑,成本為 10 小時或更少。如果同一個事件發生在這個網路中,該屬性就不會被破壞。破壞改進後的網路中相同屬性所需的變化次數比原始網路多。因此,我們可以說改進後的網路在這個屬性方面更具彈性。
如果一條鏈路的容量超過處理正常流量所需的容量,則稱其為過度配置。這種“備用容量”可以幫助鏈路,從而幫助整個網路在鏈路容量下降時保持足夠的效能水平。容量仍然會下降,但仍然能夠提供所需的 服務水平。在我們的例子中,我們可以透過升級 A-D 鏈路使其初始成本為 6 來表示過度配置。同一個導致成本增加 50% 的事件現在將導致 9 小時的成本——仍然低於 10 小時的所需服務水平。
Murry-Tuite 提出,“韌性是一種特性,表明系統在非常規條件下的效能、恢復速度以及恢復到原始功能狀態所需的外部援助量”[4] [5]。根據 Heaslip 等人的定義,“韌性是指系統在指定時間範圍內保持其已展示的服務水平或恢復到該服務水平的能力”[6] [7]。
Heaslip 還引入了韌性迴圈的概念,它包含四個階段:正常狀態、故障、自我退火和恢復[8] [9]。韌性迴圈如圖所示。

正常狀態指的是網路在沒有受到任何干擾的情況下執行,網路作為一個正常的執行系統發揮作用。在這個階段,網路具有最大的效率[10] [11]。故障階段始於干擾事件的發生。它描述了效率突然或逐漸下降的整個過程,取決於干擾事件的特性。在故障階段結束時,效率下降到最低點[12] [13]。自我退火階段緊隨故障階段,網路本身和網路使用者都試圖應對故障情況。緊急管理措施旨在緩解故障情況,網路使用者可以選擇替代路線或交通方式。網路的效率開始上升,但幅度很小[14] [15]。
恢復階段是指故障階段造成的干擾被修復,例如清除障礙物或恢復損壞的設施。恢復速度,定義為快速性,取決於恢復過程中使用的技術或資源。之後,系統可能進入一個新的正常狀態。其效率可能與原始效率相同,也可能不同[16] [17]。
韌性迴圈的圖形圖示見圖 9[18]。
該圖顯示了網路效能從舊正常狀態到新正常狀態的變化,這是由於故障階段發生的干擾造成的。干擾可以根據故障階段持續的時間分為逐步事件和突然事件。恢復線的斜率是我們之前提到的快速性。恢復後,系統可能出現三種情況:比舊正常狀態好、與舊正常狀態相同或比舊正常狀態差。實線和虛線之間的區域表示由於干擾造成的總效能損失[19]。
考慮到可以採用不同的指標來評估網路效能,因此總效能損失對於這些指標可能會有不同的表現形式,例如連通性、容量、可達性等。例如,一個具有四個節點和五條連線的網路,其連通性如圖 1、2 和 3 所示。
另一個關於容量的示例網路描述如下。該網路的圖示見 [[1]] 中的圖 4。假設在舊正常狀態下,每條連線的容量是該圖中連線旁邊顯示的值。在這個階段,網路能夠保持其效能,具有相對較高的容量來滿足交通需求。假設在連線 AD 發生了干擾,例如交通事故或道路維修,導致其容量下降至 5。當一些駕駛員選擇連線 AC 和連線 CD 從節點 A 到節點 D,而不是直接選擇連線 AD,或者網路管理開始處理這種干擾時,網路可以被視為處於自我退火階段。在事件解決後,網路可以自行恢復。此外,如果事件是為了維護道路狀況,新的正常狀態可能比舊正常狀態具有更高的效能。
- ↑ Sudakov and Vu 2008,“圖的區域性韌性”。http://www.math.ucla.edu/~bsudakov/resilience.pdf
- ↑ Sudakov 2008
- ↑ a b Newman 2003
- ↑ Murray-Tuite,Pamela M. “在模擬系統最優和使用者均衡條件下比較交通網路韌性。”模擬會議,2006 年。WSC 06。冬季會議論文集。IEEE,2006 年。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Heaslip,Kevin 等人。“一種用於評估交通網路對自然災害和人為事件韌性的草圖級方法。”交通研究委員會第 89 屆年會。編號 10-3185。2010 年。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。區域網路交通韌性的定量評估,交通研究委員會第 88 屆年會,華盛頓特區。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。區域網路交通韌性的定量評估,交通研究委員會第 88 屆年會,華盛頓特區。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。區域網路交通韌性的定量評估,交通研究委員會第 88 屆年會,華盛頓特區。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。區域網路交通韌性的定量評估,交通研究委員會第 88 屆年會,華盛頓特區。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。區域網路交通韌性的定量評估,交通研究委員會第 88 屆年會,華盛頓特區。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。
- ↑ Pant,Sunil Babu,“交通網路韌性:自我退火研究”(2012 年)。所有研究生論文和學位論文。論文編號 1434。