三角學/仰角和俯角

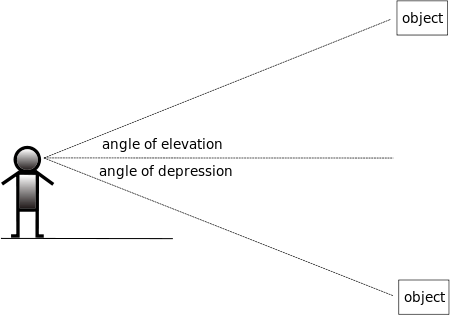
假設您是一位觀察者，位於 $O$ ，有一個物體 $Q$ ，不在同一個水平面上。設 $OP$ 是一條水平線，使得 $O,P,Q$ 在一個垂直平面上。那麼，如果 $Q$ 在 $0$ 上方，則角度 $\angle QOP$ 是從 $P$ 觀察到的 $Q$ 的 **仰角** ，如果 $Q$ 在 $O$ 下方，則角度 $\angle QOP$ 是 **俯角** 。

在使用仰角和俯角時，我們通常忽略人的高度，而是從某個方便的“地面”水平測量角度。

練習 1：對邊、斜邊、鄰邊 看上面的圖。 $\angle MLT$ 是直角。您將如何用英語翻譯這些標籤？

示例 1：旗杆 從旗杆底部 $10m$ 處，旗杆頂部的仰角為 $50^{\circ }$ 。求旗杆的高度。 [圖] 如果高度是 $h$ ，那麼 ${\frac {h}{10}}=\tan(50^{\circ })$ 。因此 $h=10\tan(50^{\circ })=11.92m$ （保留兩位小數）。

示例 2：一個 $15m$ 高的旗杆 已知一個旗杆高 $15m$ 。從什麼距離觀察，它的頂部的仰角為 $50^{\circ }$ ？ [圖] 如果距離是$d$，那麼${\frac {15}{d}}=\tan(50^{\circ })$。因此$d={\frac {15}{\tan(50^{\circ })}}=12.59m$（保留兩位小數）。

例 3：一座$20m$高的塔 從一座高$20m$的塔的底部，旗杆頂部的仰角為$30^{\circ }$。從塔頂看，旗杆頂部的俯角為$25^{\circ }$。求旗杆的高度和它到塔的距離。 設旗杆的高度為h，距離為d。則 (i) ${\frac {h}{d}}=\tan(30^{\circ })$ 由於從塔頂看，旗杆頂部的俯角，所以旗杆頂點在塔頂下方。它比塔頂低$20-h$米，所以 (ii) ${\frac {20-h}{d}}=\tan(25^{\circ })$ 將這兩個等式相加，我們得到 (iii) ${\frac {20}{d}}=\tan(30^{\circ })+\tan(25^{\circ })$ 由此（如何？）我們可以得到$d=19.16m\ ,\ h=11.06m$（均保留兩位小數）。

例 4：另一個旗杆 從某一點，旗杆頂部的仰角為$30^{\circ }$。沿著直線方向朝旗杆移動$10m$。現在旗杆頂部的仰角為$50^{\circ }$。求旗杆的高度和它到第二點的距離。 [圖] 設高度為$h$，它到第二點的距離為$x$。則 $\cot(50^{\circ })={\frac {x}{h}}\ ;\ \cot(30^{\circ })={\frac {x+10}{h}}$ 從第二個表示式中減去第一個表示式， $\cot(30^{\circ })-\cot(50^{\circ })={\frac {10}{h}}$ $h={\frac {10}{\cot(30^{\circ })-\cot(50^{\circ })}}=11.20m$ $x=h\cot(50^{\circ })=9.40m$