三角學/拍頻

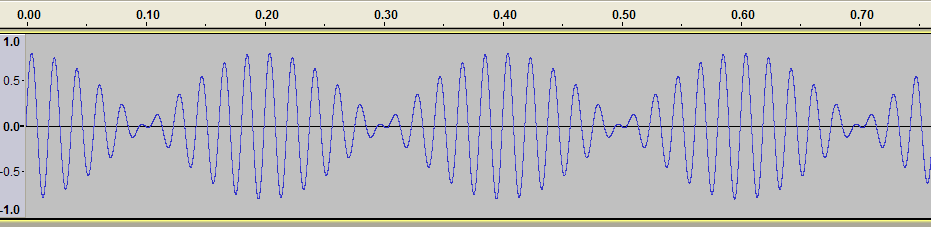
我們之前看到，當兩個波處於相位時，它們會互相加強；當它們處於反相位時，它們會互相抵消。當兩個頻率幾乎相同但並不完全相同的波疊加時，它們可能一開始會互相加強，但隨著時間的推移，頻率的差異會導致它們開始互相抵消，然後又會互相加強。

這正是上面圖形中發生的情況。它展示了一個 50 Hz 音調和一個 55 Hz 音調的疊加。它是透過在免費音訊軟體“Audacity”中混合兩個純音調生成的。影像顯示了大約 3/4 秒的音訊。在一秒鐘內，整體振幅達到最大值五次。聽這種組合的聲音，人們會聽到一個介於 50 和 55 Hz 之間的單一音調，其響度似乎每秒變化五次，即 5 Hz。你不會聽到兩個獨立的音調，一個在 50 Hz，另一個在 55 Hz。

這個 5 Hz 的音調稱為拍頻。

這裡有一個按鈕，可以播放透過組合兩個較高頻率的聲音（220 Hz 音調和 222 Hz 音調）生成的拍頻聲音。

數學

從數學上來說，我們添加了兩個頻率非常接近的聲音，但最終的結果似乎是兩個頻率非常不同的聲音的乘積。這些頻率是什麼？一個是平均值，即 52.5 Hz。另一個乍一看似乎是差值，即 5 Hz，但實際上是差值的一半，因為一個 5 Hz 的正弦波在一秒鐘內會達到最大值（忽略正負號）十次。

所以，一個頻率是差值的一半，另一個頻率是平均值。我們可以使用正弦的加法公式來理解從數學上來說，兩個正弦的和如何變成一個積（正弦和餘弦的積）。

我們新增的單個波形是

$\displaystyle \sin(\lambda _{1}t)$ $\displaystyle \sin(\lambda _{2}t)$

$\displaystyle \lambda _{1}=50\times 2\pi$ $\displaystyle \lambda _{2}=55\times 2\pi$

以及

為了得到 50 Hz 和 55 Hz 的頻率，我們可以將

$\displaystyle \sigma =(\lambda _{1}+\lambda _{2})/2$

$\displaystyle h=(\lambda _{1}-\lambda _{2})/2$

然後用這兩個新變數重新表達 $\displaystyle \lambda _{1}$ 和 $\displaystyle \lambda _{2}$。

$\displaystyle \lambda _{1}=\sigma +h$

$\displaystyle \lambda _{2}=\sigma -h$

現在我們有

$\displaystyle \sin(\lambda _{1}t)=\sin(\sigma t+ht)=\sin(\sigma t)\cos(ht)+\cos(\sigma t)\sin(ht)$

$\displaystyle \sin(\lambda _{2}t)=\sin(\sigma t-ht)=\sin(\sigma t)\cos(ht)-\cos(\sigma t)\sin(ht)$

在驗證這兩個公式是否遵循正弦加法公式之前，請勿繼續閱讀本頁！不檢查步驟就閱讀本頁並不能幫助你更好地使用數學。

因此，我們可以將這兩個公式結合起來，得到

$\displaystyle \sin(\lambda _{1}t)+\sin(\lambda _{2}t)=2\sin(\sigma t)\cos(ht)$

也就是說

$\displaystyle \sin(\lambda _{1}t)+\sin(\lambda _{2}t)=2\sin \left({\frac {(\lambda _{1}+\lambda _{2})t}{2}}\right)\cos \left({\frac {(\lambda _{1}-\lambda _{2})t}{2}}\right)$

我們將兩個正弦波的和表示為正弦和餘弦的乘積。正如預期的那樣，正弦波的頻率是兩個被組合波頻率的平均值，而餘弦波的頻率是頻率差的一半。