三角學/圓和三角形/外接圓

三角形的外接圓是經過三角形三個頂點的唯一圓形。

外接圓的圓心稱為外心。它是三條邊的垂直平分線的交點。這可以透過以下方式解釋

• 每條邊的垂直平分線是到邊兩端點距離相等的點的軌跡，例如，${\overline {AB}}$ 的垂直平分線上的所有點都與點 A 和點 B 的距離相等。
• 在 ${\overline {AB}}$ 的垂直平分線上，點到 A 和 B 的距離相等。在 ${\overline {BC}}$ 的垂直平分線上，點到 B 和 C 的距離相等。這兩條垂直平分線相交的點到 A 和 B 的距離相等，並且到 B 和 C 的距離相等。因此，該交點的距離到 A 與它到 B 的距離相等，也與它到 C 的距離相等。因此，它到 A 和 C 的距離相等，因此它位於 ${\overline {AC}}$ 的垂直平分線上。
• 三條垂直平分線相交的點到 A、B 和 C 的距離相等。因此，以該點為圓心的圓形可以經過所有三個點。

• 
  銳角三角形的外心位於三角形內部
• 
  直角三角形的外心位於斜邊上
• 
  鈍角三角形的外心位於三角形外部

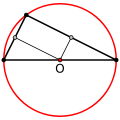
該圓形的半徑（外接圓半徑，通常用 R 表示）如下求得：如果 a 是三角形的任何一邊，A 是該邊所對的角，則 $R={\frac {a}{2\sin(A)}}$。為了證明這一點，考慮一個三角形，其中兩條邊是外接圓的半徑，第三條邊是長度為 a 的邊。該三角形是等腰三角形（因為所有半徑的長度都相等），兩條半徑之間的夾角是 2A，因為圓心角是圓周角的兩倍。該公式從對該三角形的簡單三角函式應用得出。

根據正弦定理，從所有三邊都可以得到相同的 R 值。

如果另外兩條邊是 b 和 c，則三角形的面積 Δ 為 ${\frac {bc}{2}}\sin(A)$。將這兩個公式相乘，得到 $\Delta R={\frac {abc}{4}}$。

用 2Rsin(A) 等替換 a，得到

Δ = 2R²sin(A)sin(B)sin(C)。

當且僅當所有角都為銳角時，外心位於三角形內部。對於直角三角形，它位於斜邊的中點；如果有一個角為鈍角，它位於三角形外部。外接圓是包含銳角三角形的最小圓形。對於鈍角三角形，以最長邊為直徑的圓形更小。（對於直角三角形，這兩個圓形相同。）