三角學/愛好者/嚴格的三角學
此頁面最初作為三角學最基本概念的介紹,例如測量角度。做得恰當,這將是一個高階主題。此頁面現在已移動/重新命名為第 3 冊,以承擔該角色,並且需要進行大量修訂。某些仍然在此處的內容可能需要重新整合到第 1 冊中 |

當兩條直線相交時形成一個角;交點稱為頂點。我們可以將角視為兩條直線相遇時之間的楔形空間。請注意,如果兩條直線都透過交點延伸,實際上有四個角。
角的大小是兩條直線之間旋轉的度數。我們必須旋轉一條直線以與另一條直線相遇的次數越多,角度就越大。
假設您想精確地測量兩條直線之間的角度,以便可以告訴遠處的朋友:在兩條直線相遇處畫一個圓,確保圓足夠小以穿過兩條直線,但足夠大以讓您測量圓邊緣的距離,即圓周,在兩個交叉點之間。顯然,此距離取決於圓的大小,但只要您告訴您的朋友所用圓的半徑和圓周上的長度,您的朋友就可以精確地重建角度。
角度是由繞其端點旋轉射線確定的。射線的起始位置稱為角的始邊。射線的結束位置稱為終邊。射線的端點稱為其頂點。正角是由逆時針旋轉產生的。負角是由順時針旋轉產生的。
因此,角度有四個部分:它的頂點、它的始邊、它的終邊和它的旋轉。
當角度以使它的頂點位於原點,而它的始邊為正 x 軸的方式在笛卡爾座標系中繪製時,據說它處於標準位置。

三角形是一種具有三條直邊的平面(扁平)形狀。在三角形的每兩條邊之間形成一個角,三角形有三個角,因此得名三-角。因此,三角形有三個直邊和三個角。
如果你給我三個長度,我只能用它們組成一個三角形,前提是最大長度小於另外兩個長度的總和。不能構成三角形三條邊的三個長度是你的身高,最近樹的高度,從樹頂到太陽中心的距離。
角度不受直線長度的影響:角度在縮放變換下是不變的,也就是說
如果你使三角形變大,
但保持邊之間的比率相同,
它的角度不會改變。
一個特別重要的角度是直角:正方形或長方形每個角的角度。長方形總是可以透過從長方形的一個角到對角線畫一條線來分成兩個三角形。
每個直角三角形都是長方形的一半也是正確的。

長方形有四條邊;它們通常有兩種不同的長度:兩條長邊和兩條短邊。(所有邊都相等的長方形是正方形。)當我們將長方形分成兩個直角三角形時,每個三角形都具有長方形的長邊和短邊,以及分裂線的副本。
因此,直角三角形的面積是將它分割的長方形面積的一半。看一個直角三角形,我們可以知道該長方形的長邊和短邊是什麼;它們是直角相交的邊,即直線。完整長方形的面積是長邊乘以短邊。因此,直角三角形的面積是一半。

可以使用以下步驟僅使用圓(可以使用圓規繪製)和直線來平分任何角
- 將角的頂點稱為 O。以 O 為中心畫一個圓。
- 標記圓與每條射線的交點。將這些點稱為 A 和 B。
- 以 A 和 B 為中心畫圓,半徑相等,但確保這些半徑足夠大以使圓在兩點處相交。一種肯定的方法是繪製線段 AB 並使圓的半徑等於該線段的長度。在圖中,圓 A 和 B 顯示為圓的近一半部分。
- 標記這些圓的交點,並將這兩個點用一條直線連線起來。這條直線平分了原始角。
在《幾何原本》的第 1 卷命題 9中可以找到這條線平分角的證明。
給定一個直角,我們可以使用此過程無限地分割該直角以形成任何二進位制分數(即 ,例如 )。因此,我們可以用直角來測量任何角度。也就是說,在一個測量系統中,直角的大小被認為是 1。
為了說明弧度的三條邊是如何相互關聯的,請嘗試以下思維實驗。
- 假設你有一根繩子,它的長度正好等於圓的半徑。
- 假設你在同一個圓中畫了一個弧度。弧度有三個點。一個是圓心,另外兩個是在圓周上,弧度的邊與圓相交的地方。
- 將繩子的一端固定在弧度與圓周相交的點之一上。
- 拿起繩子的另一端,從你在上面步驟 2 中選擇的點開始,沿著圓周向弧度與圓周相交的第二個點移動,直到繩子拉緊。
- 你會看到繩子的末端會經過第二個點。
- 這是因為繩子現在是一條直線。然而,弧度的第三邊是弧線,而不是直線。即使弧度有三條相等的邊,弧線的彎曲也導致弧度與圓周相交的兩個點比它們到三角形第三個點的距離更近,在這個例子中,三角形的第三個點是圓心。
- 現在,在繩子仍然拉緊的情況下,找到繩子的中點,然後將其拉到圓周上,同時允許繩子的末端沿著圓周移動。繩子的末端現在更靠近第二個點,因為繩子的路徑更接近圓周的路徑。
- 我們可以透過將繩子的每個新部分分成兩半並將其拉向圓周,來不斷改善繩子路徑與圓周路徑的吻合度。
使用不同大小的圓來測量弧度是否會產生不同的角度?也許使用大圓的半徑會產生與使用小圓的半徑產生的角度不同的角度。答案是否定的。

回想我們在上面小節中的弧度和圓。在第一個圓內畫一個半徑為第一個圓半徑一半的第二個圓,並與第一個圓共用圓心。你會看到你在較小的圓內建立了一個新的弧度,該弧度與較大圓內的弧度具有相同的角度。我們知道從圓心出發的弧度的兩條邊等於它們各自圓的半徑。我們也知道較大圓的弧度的第三邊(弧線)也等於較大圓的半徑。但是我們怎麼知道較小圓的弧度的第三邊(沿著較小圓圓周的弧線)等於較小圓的半徑呢?為了說明我們為什麼知道較小圓的弧度的第三邊等於它的半徑,我們首先將每個弧度與圓相交的兩個點彼此連線起來。透過這樣做,你將建立兩個等腰三角形(有兩條相等的邊和兩個相等的角)。
等腰三角形有兩個相等的角和兩條相等的邊。如果你知道任何等腰三角形的一個角和組成該角的兩條邊的長度,那麼你就可以很容易地推匯出等腰三角形的剩餘特徵。例如,如果等腰三角形的兩條等邊相交形成一個等於 40o 的角,那麼你知道剩下的兩個角都必須等於 70º。由於我們知道我們兩個等腰三角形的等邊構成了我們已知的角度,那麼我們可以推斷出我們兩個弧度(當轉換成帶有直線的等腰三角形時)具有相同的第二和第三個角。我們還知道具有相同角度的三角形,無論它們的大小如何,它們的邊長都將保持一個恆定的比例。例如,我們可以推斷出一個等腰三角形的邊長將分別為 2 米、4 米和 4 米,如果我們知道一個具有相同角度的等腰三角形的邊長分別為 1 米、2 米和 2 米。因此,在我們的例子中,由第二個較小的圓形成的等腰三角形的第三邊將正好等於由較大圓形成的等腰三角形的第三邊的一半。共享相同角度的兩個三角形的邊長之間的關係,也存在於共享相同中心的兩個圓的半徑和周長之間的關係中——它們將共享完全相同的比例。那麼,在我們的例子中,由於我們的第二個較小的圓的半徑正好是較大圓的一半,因此較小圓的弧度與圓周相交的兩個點之間的周長(我們已經證明它是較大圓上兩個類似點之間的距離的一半)將共享完全相同的比例。就這樣——圓的大小並不重要。
一旦我們有了 1 個弧度的角度,我們就可以將其分割成二進位制分數,就像我們對直角所做的那樣,得到一系列已知角度,用來測量未知角度。量角器是一種利用這種技術近似測量角度的工具。要使用量角器測量角度:將量角器上標記的中心點放在要測量的角度的角上,將量角器上的右手零弧度線與角度的一條線對齊,然後讀出角度的另一條線與量角器邊緣的交點。量角器通常是透明的,上面畫有角度線,可以幫助你測量由短線形成的角度:這是允許的,因為角度不依賴於形成它們的線的長度。
如果我們同意用弧度測量角度,那麼知道一些容易定義的角度的大小將很有用。當然,我們可以簡單地畫出角度,然後使用量角器非常精確地測量它們,儘管仍然只是近似值:但是,那樣我們就是在做物理,而不是數學。
圓的周長與半徑的長度之比定義為 2π,其中π是根據上面論證,不依賴於圓的大小的一個不變數。因此,如果我們從圓周上的一個給定點沿著圓周移動 2π 個半徑,我們就會回到起點。我們必須得出結論,繞圓周執行一週形成的角度的大小為 2π 弧度。同樣,繞圓周執行半周將是 π 弧度。想象一下,將一個圓沿著對稱軸對摺:形成的摺痕將是一條直徑,一條穿過圓心的直線。因此,直線具有 π 弧度的角度。
再次將半圓對摺,會得到一個四分之一圓,因此它的角度大小必須是 π/2 弧度。四分之一圓是一個直角嗎?為了說明它是直角:畫一個正方形,其角點位於圓周上。畫出連線正方形對角的斜線,由於對稱性,它們將穿過圓心,形成 4 個相似的三角形。每個這樣的三角形都是等腰三角形,並且在兩條等長邊在圓心相遇的地方有一個 π/2 弧度的角。因此,三角形的另外兩個角必須相等,並且總和為 π/2 弧度,也就是說每個角的大小都必須是 π/4 弧度。我們知道這樣的三角形是直角三角形,我們必須得出結論,π/2 弧度的角度確實是直角。
總之:可以使用幾何論證來推斷某些特殊情況下角度的大小。但是,一般而言,僅靠幾何不足以確定任何任意三角形中未知角度的大小。為了解決這些問題,我們需要藉助三角函式。
原則上,所有角度和三角函式都在單位圓上定義。在數學中,術語“單位”指的是任何長度的單個測量值。我們將在以後將從單位測量中獲得的原理應用於更大(或更小)比例的問題。我們需要的函式都可以從內接於單位圓的三角形中推匯出:它恰好是一個直角三角形。
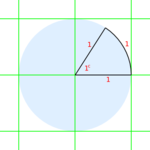
單位圓的中心點將設定在一個笛卡爾平面上,圓心位於平面的原點——點 (0,0)。因此我們的圓將被分成四個部分,或象限。
象限總是按逆時針方向計數,就像角速度 (omega)的預設旋轉方向一樣。現在我們在第一象限(即 x 軸和 y 軸分配正值的象限)中內接一個三角形,並讓角度的一條邊在 x 軸上,另一條邊平行於 y 軸。(只需檢視插圖以進行澄清)。現在我們讓斜邊(始終為 1,即我們的單位圓的半徑)逆時針旋轉。你會注意到,當我們進入一個新的象限時,會形成一個新的三角形,不僅因為三角形的角度之和不能超過 180°,而且因為在二維平面上無法想象其他情況。




