使用算盤/現代除法

引言和最初的方法

歐幾里得除法

如果我們考慮兩個自然數 $a$ 和 $b$ ， $a$ 除以 $b$ （表示為 $a/b$ 或 $a\div b$ ）回答了數字 $b$ 在數字 $a$ 中包含了多少次的問題。在 $a/b$ 中的數字 $a$ 稱為被除數， $b$ 稱為除數。答案稱為商。

讓我們以 $a=1225$ 和 $b=35$ 為例。除了重複減法並計算我們從被除數中減去除數的次數之外，沒有更簡單的方法來回答這個問題。我們可以使用算盤上的一個列作為計數器來直接進行操作。

1225÷35 = 35，原始方法
算盤	註釋
ABCDEFGHIJKL
35 1225
+1 -35	從KL減去35，在計數器F中加1
35 1 1190
+1 -35	從KL減去35，在計數器F中加1
35 2 1155
+1 -35	從KL減去35，在計數器F中加1
35 3 1120
...	繼續再進行33次...
35 33 70
+1 -35	從KL減去35，在計數器F中加1
35 34 35
+1 -35	從KL減去35，在計數器F中加1
35 35 00	完成，商數在EF中為35！

因此，我們發現數字 $35$ 在 $1225$ 中正好包含了 $35$ 次，因為我們不能繼續減去 $35$ 而不會開始處理負數。因此，在這個例子中，商是： $q=35$ 。

正如我們所看到的，在這種情況下，我們可以寫成 $1225=35\times 35$ 或者

$a=q\times b$

我們不能期望在一般情況下都能如此。如果我們用 $a=1240$ 重複這個過程，我們會看到，在減去 $35$ 乘以 $35$ 次後，算盤上會剩下 $15$ ，我們不能繼續減去 $35$ 而不會進入負數。因此，我們有 $1240=35\times 35+15$ ；也就是說，將 $1240$ 除以 $35$ 的結果是商為 $35$ ，餘數為餘數 $15$ 。一般情況下，我們將有

$a=q\times b+r$

其中

$a$ ：被除數
$b$ ：除數
$q$ ：商
$r$ ：餘數

如果餘數為零，則被除數是除數的倍數。

這就是歐幾里得除法在自然數上的概念，小數除法可以簡化為自然數除法。

一些改進：分塊方法

上一節中採用的方法在概念上是最簡單的，但它極其冗長且效率低下。與其直接從被除數中減去除數 $b$ ( $35$ ) 開始，我們先考慮從被除數中減去除數的多少倍的10次冪；在我們的例子中：我們可以減去3500、350，還是隻能減去35？顯然我們可以減去350，我們將開始減去350個“塊”，當我們無法繼續時，我們將開始減去35個“塊”，如下所示

1225÷35 = 35，這是一個很大的改進
算盤	註釋
ABCDEFGHI
35 1225	開始，計數器在D處，
35 1 875	從GH中減去35，將計數器D加1，
35 2 525	從GH中減去35，將計數器D加1，
35 3 175	從GH中減去35，將計數器D加1，
35 31140	從HI中減去35，將計數器E加1，
35 32105	從HI中減去35，將計數器E加1，
35 33 70	從HI中減去35，將計數器E加1，
35 34 35	從HI中減去35，將計數器E加1，
35 35 00	從HI中減去35，將計數器E加1。
35 35	沒有餘數。完成，商為35！

這快多了（我們有意儘可能縮短計數器和被除數之間的距離。這在某種程度上模糊了過程，但使我們更接近於我們將在現代除法方法中常規執行的操作。請仔細研究以上計算，並使用你自己的算盤）。讓我們從這裡繼續，尋找更高的效率。

如果我們能夠輕鬆地將除數加倍並在記憶中保留它，那麼我們可以透過減去一到兩個除數“塊”來縮短運算。

倍	塊
1	35
2	70

1225÷35 = 35，更復雜的方法
算盤	註釋
ABCDEFGHI
35 1225	開始，計數器在D處，
35 2 525	從GH中減去70，將計數器D加2，
35 3 175	從GH中減去35，將計數器D加1，
35 32105	從HI中減去70，將計數器E加2，
35 34 35	從HI中減去70，將計數器E加2，
35 35 00	從HI中減去35，將計數器E加1。
35 35	沒有餘數。完成，商為35！

或者，如果我們可以像下面這樣透過將除數加倍三次來構建一個表格，則會更好^[1]

倍	塊
1	35
2	70
4	140
8	280

1225÷35 = 35，一種非常有效的方法
算盤	註釋
ABCDEFGHI
35 1225	開始，計數器在D處，
35 2 525	從GH中減去70，將計數器D加2，
35 3 175	從GH中減去35，將計數器D加1，
35 34 35	從HI中減去140，將計數器E加4，
35 35 00	從HI中減去35，將計數器E加1。
35 35	沒有餘數。完成，商為35！

這稍微簡短一些，而且顯然，沒有什麼比擁有除數的完整乘法表更快了

乘法表

35的乘法表
倍	塊
1	35
2	70
3	105
4	140
5	175
6	210
7	245
8	280
9	315

然後

1225÷35 = 35，最短的方法！
算盤	註釋
ABCDEFGHI
35 1225	開始，計數器在D處，
35 3 175	從GH中減去105，將計數器D加3，
35 35 00	從HI中減去175，將計數器E加5。
35 35	沒有餘數。完成，商為35！

毫無疑問，這是一種最佳的除法方法，一旦我們有了像上面那樣的“塊”表，就沒有什麼比它更快更方便的了。但是計算“塊”表很費時間，需要紙和筆來書寫，只有當我們需要對同一個除數進行大量的除法運算時，這項額外的工作才值得。

1617年，對數之父約翰·納皮爾提出了他的發明來解決這個問題，該發明由一系列被稱為納皮爾算籌的算籌組成，上面寫著一位數的乘法表，這些算籌可以組合起來得到任何數的乘法表。例如，在我們的例子中

使用納皮爾算籌計算35的乘法表
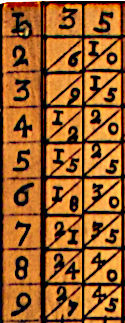
	1	35
	2	70
	3	105
	4	140
	5	175
	6	210
	7	245
	8	280
	9	315

毫無疑問，這樣的發明傳播到了東方，並與算盤一起使用，但這種用法必須被認為是例外的；並非每個人都能隨時隨地使用納皮爾算籌。需要另一種工具，那就是傳統的一位數乘法表，它是死記硬背下來的，我們將用它來近似表示除數的特定乘法表（上面使用的那個），這個表將指導我們選擇必須嘗試的商的數字。

需要注意的是，以上過程並沒有窮盡分塊方法的所有可能性。如果你閱讀了《整數長除法的權威高等數學指南》^[2]文章，你將會對可以執行的各種除法方法感到驚訝。

現代除法

現代除法與傳統除法

現代除法方法之所以被稱為現代，是因為在整個20世紀上半葉，它的使用取代了傳統方法，但實際上它比這古老得多，在13世紀被傳統方法取代。現代方法的一個特點是使用一位數乘法表作為我們必須嘗試的中間商數的選擇指南，以及計算我們必須從被除數中減去的“塊”。

十進位制乘法表
×	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

相比之下，傳統方法既使用特殊的除法表作為中間商數的指南，也使用乘法表來計算要減去的“塊”。

明治維新後，現代方法在日本開始取代傳統方法的主要原因是，對於那些已經掌握了紙筆除法的人來說，它更容易更快地學習，因為它不需要記憶複雜的除法表。另一方面，傳統方法使除法成為一個完全自動化的過程，無需思考，只需要遵循規則即可得到結果，從而使操作無需任何腦力疲勞。如果你對這個話題感興趣，可以參考華夏公益教科書：傳統算盤和珠算。

算盤除法的關鍵點

學習算盤的關鍵點之一是要意識到，這種工具使我們能夠非常快速地糾正一些錯誤，並且不留下痕跡，這使得算盤成為一種特別適合試錯過程的工具。這在除法的情況下尤其有用。因此，如果我們必須計算634263÷79283，我們不必絞盡腦汁去尋找正確的商數，只需透過將原始問題簡化為63÷7來選擇一個近似的臨時或中間數字，然後透過嘗試從被除數中減去“塊”（中間商數）✕79283來測試它；以下情況之一將會發生

中間商數是正確的: 也就是說，我們可以減去“塊”（中間商數）✕（除數）而不會出現負數，但我們不能再減去一次商數，因為餘數小於除數。
它是不夠的，我們需要向上修正: 我們可以減去“塊”（中間商數）✕（除數）而不會出現負數，但我們仍然可以再減去一次商數，因為餘數大於/等於除數。我們將中間商數加1，然後再次從餘數中減去除數。
它是過大的，我們需要向下修正: 這是最複雜和最容易出錯的情況。我們通常在（減去“塊”的過程中）發現得太晚，中間數字過大，我們需要回退，將商數減1，並透過加上多減的部分來恢復被除數/餘數，然後才能繼續。

因此，獲得商數的一個數字的過程有兩個階段

選擇一箇中間商數。
測試它是否正確，如果不正確則修改它。

一旦我們找到了正確的數字，我們通常會得到一個非零的餘數，如果我們想將除法擴充套件到商數的下一位，這個餘數將充當被除數。

我們將在接下來的示例中看到所有這些，但首先，我們需要簡單介紹一下如何在算盤上組織除法。

現代除法排列

被除數是我們在算盤上要操作的活動項，除數是不活動的，在操作過程中保持不變，事實上，它不需要輸入到算盤中，但建議這樣做，尤其對於初學者來說。與乘法一樣，在算盤上放置被除數和除數有兩種方式，每種方式都有其優點和缺點。

傳統中式排列

除數放在算盤的最右邊，而被除數放在左邊，在其左邊至少留出兩列空位。

**1225÷35 中式排列**
A	B	C	D	E	F	G	H	I	K	J	L	M

		1	2	2	5						3	5

傳統日式排列

除數位於算盤的最左邊，被除數在其右邊，兩項之間至少留出四列空位。

**1225÷35 日式排列**
A	B	C	D	E	F	G	H	I	K	J	L	M

3	5					1	2	2	5

本書中，示例將使用日式風格，但您可以隨意嘗試兩種方法。

放置商數

中間商數放置在被除數左側的兩列之一。為了確定哪一列，我們需要將除數與被除數前幾位數相同的數字進行比較，如果需要，在其右側新增零；稱之為**工作被除數**。

工作被除數大於或等於除數: 這意味著除數可以整除工作被除數，商數（即除數可以整除工作被除數的次數）排列在被除數第一位數字左側的第二列。; **示例**：827÷46，工作被除數82大於46，則中間商數位於被除數左側的第二列。乘法表建議我們使用**2**作為中間商數（將827÷46簡化為8÷4）

827÷46
算盤	註釋
ABCDEFGHIJKLM
46 827
46 2 827	將中間商數2放在E列

工作被除數小於除數: 這意味著除數不能整除工作被除數。在這種情況下，我們需要將被除數的下一位數字（如果沒有剩餘數字，則為零）包含在我們的工作被除數中，商數（即除數可以整除此擴充套件工作被除數的次數）排列在被除數第一位數字左側的列中。; **示例**：18÷467，180小於467，則工作被除數為1800，中間商數位於被除數左側的第一列。乘法表建議我們使用**4**作為中間商數，在將1800÷467簡化為18÷4之後。

標題文字
算盤	註釋
ABCDEFGHIJKLM
467 18
467 418	將中間商數4放在G列

示例

您應該先進行一位數除數的練習，然後再嘗試兩位數、三位數等的除數。對於一位數除數，您永遠不需要向上或向下修正。例如，您可以將123456789除以數字2、3、…、9。讓我們在這裡看看除以9的情況。

示例：123456789÷9 = 13717421

請將“->”符號理解為：“乘法表建議使用…”。
您會看到，在除最後一個之外的所有情況下，工作被除數都小於除數，我們需要將其擴充套件到兩位數。

123456789÷9 = 13717421
算盤	註釋
ABCDEFGHIJKLMNO
9 123456789	12/9 -> 1 作為中間商數
9 1123456789	將中間商數放在E列
-9	從FG列減去9✕1=9
9 1 33456789	33/9 -> 3 作為中間商數
9 1333456789	將中間商數放在F列
-27	從GH列減去9✕3=27
9 13 6456789	64/9 -> 7 作為中間商數
9 1376456789	將中間商數放在G列
-63	從HI列減去9✕7=63
9 137 156789	15/9 -> 1 作為中間商數
9 1371156789	將中間商數放在H列
-9	從IJ列減去9✕1=9
9 1371 66789	66/9 -> 7 作為中間商數
9 1371766789	將中間商數放在I列
-63	從JK列減去9✕7=63
9 13717 3789	37/9 -> 4 作為中間商數
9 1371743789	將中間商數放在J列
-36	從KL列減去9✕4=36
9 137174 189	18/9 -> 2 作為中間商數
9 1371742189	將中間商數放在K列
-18	從LM列減去9✕2=18
9 1371742 9	9/9 -> 1 作為中間商數
9 13717421 9	將中間商數放在L列
-9	從MN列減去9✕1=9
9 13717421	沒有餘數！完成 123456789÷9 = 13717421

123456789是一個有趣的數字，它恰好是9乘以13717421的積，後者是一個很大的質數！

示例：1225÷35 = 35 兩位數除數。向下和向上修正

1225÷35 = 35
算盤	註釋
ABCDEFGHIJ
35 1225	12÷3↦4 作為中間商數
+4	將中間商數輸入F列
35 41225	現在嘗試從GHI列減去4✕35的部分積，
-12	首先從GH列減去4✕3
35 40025	然後從HI列減去4✕5
-20	無法減去！
-1	向下修正中間商數的數字
35 30025
+3	將從GH列減去的多餘部分返回^a
35 30325
-15	繼續正常操作，從HI列減去3✕5
35 3 175	17÷3↦5 作為中間商數
+5	將中間商數輸入G列
35 35175	嘗試從HIJ列減去5✕35的部分積
-15	首先從HI列減去5✕3
35 35025
-25	然後從IJ列減去5✕5
35 35	沒有餘數，完成！1225÷35 = 35

注意：^a 我們已經從FGH列減去了4 × 3 = 12，但如果正確的商數數字是3，我們應該減去3 × 3 = 9，所以我們多減去了3（只是除數的第一位數字）。在繼續之前，我們必須將這個多減的部分返回。

現在，假設在我們“糟糕的經歷”之後，向下修正了商數的第一位數字，並且出於謹慎，我們選擇4作為第二個中間商數，而不是乘法表建議的5。然後我們繼續這樣操作

1225÷35 = 35，第二個商數數字，向上修正的示例
算盤	註釋
ABCDEFGHI
35 3 175	17÷3 -> 5，但我們使用4！
+4	將中間商數輸入G列
35 34175	嘗試從HIJ列減去4✕35的部分積
-12	首先從HI列減去4✕3 = 12
-20	然後從IJ列減去4✕5 = 20
35 34 35	餘數大於或等於除數！
+1	向上修正G列
-35	從餘數HI列減去除數
35 35	沒有餘數，完成！

示例 1÷327

到目前為止，我們已經考慮了自然數之間的除法，包括商數和餘數以及自然數，但我們可以像在用長除法進行書面計算時那樣，完全使用小數進行運算。例如，讓我們在有13列的算盤上求327的倒數；即，1/327。

1÷327 = 0.00305810...
算盤	註釋
ABCDEFGHIJKLM
327 1	10/3 -> 3 作為中間商數
327 31	將中間商數輸入G列
-09	從HI列減去3✕3=9
327 3 1
-06	從IJ列減去3✕2=6
327 3 4
-21	從JK列減去3✕7=21
327 3 19	19/3 -> 6 作為中間商數
327 30619	將中間商數輸入I列
-18	從JK列減去6✕3=18
327 306 1
-12	無法減去6✕2=12 從KL列！
-1	向下修正I列
+3	將從JK列減去的多餘部分返回
327 305 4
-10	繼續正常操作，從KL列減去5✕2=10
327 305 30
-35	從LM列減去5✕7=35
327 305 265	36/3 -> 8 作為中間商數
327 3058265	將中間商輸入到J柱
-24	從KL柱減去8✕3=24
327 3058 25
-16	從LM柱減去8✕2=16
327 3058 9	無法繼續！結果：3058

我們已經得到了 $3058$ 作為 $1/327$ 的前幾位數字，但是 $1/327\approx 1/300=1/(3\cdot 100)=(1/3)\cdot 0.01\approx 0.33\cdot 0.01=0.0033$ ，所以我們的結果實際上是 $0.003058$ 。請參見下文關於如何找到除法中個位數所在位置的規則。

示例：634263÷79283 = 7,999987...，一個棘手的例子

最後，讓我們求出這個特別惡意的除法商的第一位數字

634263÷79283 = 7,999987...
算盤	註釋
ABCDEFGHIJKLM
79283 634263	63/7 -> 試9
79283 9634263
-63	從HI柱減去9*7=63
79283 9004263
-81	無法減去9*9=81從IJ柱！
-1	向下修正D柱
+7	恢復從餘數中減去的過多部分
79283 8 74263
-72	繼續從IJ柱減去8x9=72
79283 8 02263
-16	從JK柱減去8*2=16
79283 8 00663
-64	從KL柱減去8*8=64
79283 8 00023	無法減去8*3=24從LM柱！
-1	向下修正D柱
+7928	恢復從餘數中減去的過多部分
79283 7 79303
-21	繼續從LM柱減去7x3=21
79283 7 79282	商：7，餘數：79282

毫無疑問，在這種情況下，將除數79283四捨五入到80000會給我們帶來更好的結果，因為63÷/8建議使用7（正確數字）作為中間商數字。

634263÷79283 = 7,999987...，四捨五入除數
算盤	註釋
ABCDEFGHIJKLM
79283 634263	63/8 -> 試7
7634263
-49	從HI柱減去7*7=49
79283 7144263
-63	從IJ柱減去7*9=63
79283 7 81263
-14	從JK柱減去7*2=14
79283 7 79863
-56	從KL柱減去7*8=56
79283 7 79303
-21	從LM柱減去7*3=21
79283 7 79282	商：7，餘數：79282

個位數和十進位制

尋找乘法中個位數所在位置的規則的對應規則是除法中的以下規則

商的個位數所在列位於被除數的個位數所在列的左側

n+1

列；其中

n

是被除數小數點左側的數字個數（可以為負數！）。

下表顯示了一些除數的 $n$ 值


乘數	n
32.7	2
3.27	1
0.327	0
0.00327	-2

示例：1/327（我們在上面已經看到過）

1/327個位數
算盤	註釋
ABCDEFGHIJKLM
327 1	除數有3位數。n=3
.	被除數個位數
...
327 3058 9	除法結束。結果：3058
.	被除數個位數
<---	將其向左移動n+1 = 4個位置
.	商的個位數
3058	以便這個...
.003058	...應該讀作0.003058

乘法和除法作為互逆運算

在書面計算中，我們總是可以複查我們的計算，以確保我們沒有犯錯誤，並且獲得的結果是正確的。在使用算盤進行計算時，這是不可能的，因為算盤不會保留過去和中間結果的記憶。我們可以求助於一些健全性測試，例如九去法或十一去法，但使用算盤檢查結果的傳統方法一直是重複計算或撤消計算。

撤消加法和減法就像從結果開始，減去我們加過的數，加上我們減過的數一樣簡單；如果我們正確地進行計算和驗證，我們應該最終得到一個重置的算盤。為了驗證乘法，我們將使用除法，反之亦然，為了驗證除法，我們將使用乘法，加上如果有的話的餘數。完成此操作後，我們將算盤恢復到其初始狀態，並將兩個原始運算元恢復到其初始位置。讓我們看一個例子

透過乘法測試2461÷64
算盤	註釋
ABCDEFGHIJ
64 2461	24/6 -> 4作為中間商
42461	將中間商數輸入F列
-24	從GH柱減去4✕6=24
64 4 61
-16	無法從HI柱減去4✕4=16
-1	向下修正中間商數字
64 3 61
+6	將從GH柱減去的過多部分返回
64 3 661
-12	繼續正常操作，從HI柱減去3✕4=12
64 3 541	54/6 -> 9，但我們將使用8
64 38541
-48	從HI柱減去8✕6=48
64 38 61
-32	從IJ柱減去8✕4=32
64 38 29	商：38，餘數29
	透過乘法進行復查從這裡開始！
+48	將8✕6=48加到HI柱
64 38509
+32	將8✕4=32加到IJ柱
64 38541
64 3 541	清零G柱
+18	將3✕6=18加到GH柱
64 32341
+12	將3✕4=12加到HI柱
64 32461
64 2461	清零F柱。初始狀態！

本書建議在使用一位數進行乘法和除法的第一次練習中使用數字123456789。嘗試將其與反運算結合起來；例如：將123456789除以9得到13717421，並將此結果乘以9得到123456789，回到算盤上的相同起始位置。或者從將123456789乘以9開始得到1111111101，然後除以9回到起點。嘗試從2到9的所有數字。

參考文獻

↑ Wilson, Jeff. "長除法教學輔助，"雙除法"". 雙除法. 存檔於原始檔案，於 2021年3月2日。 {{cite web}}: 請檢查日期值：|archivedate= (幫助); 忽略了“2005年”文字 (幫助); 忽略了未知引數|accesdate= (|access-date= 建議) (幫助)
↑ "關於整數長除法（及其變體）的權威高等數學指南". 數學保險庫. 存檔於原始檔案，於 2021年5月14日。 {{cite web}}: 忽略了未知引數|accesdate= (|access-date= 建議) (幫助); 忽略了未知引數|name= (幫助)

外部連結

練習題

"生成器". 練習算盤. {{cite web}}: 忽略了未知引數|accesdate= (|access-date= 建議) (幫助)

進一步閱讀

Kojima, Takashi (1954), "除法", 日本算盤：其使用和理論, 東京：查爾斯·E·塔特爾公司，ISBN 978-0-8048-0278-9
Heffelfinger, Totton (2004). "除法". 算盤：珠子的奧秘. 存檔於原始檔案，於 2021年6月29日。 {{cite web}}: 忽略了未知引數|accesdate= (|access-date= 建議) (幫助)
Siqueira, Edvaldo (2004). "小數和除法". 算盤：珠子的奧秘. 存檔於原始檔案，於 2021年5月6日。 {{cite web}}: 忽略了未知引數|accesdate= (|access-date= 建議) (幫助)

下一頁：使用算盤 | 上一頁：現代乘法
首頁：使用算盤

[IDchunk-1] Wilson, Jeff. "長除法教學輔助，"雙除法"". 雙除法. 存檔於原始檔案，於 2021年3月2日。 {{cite web}}: 請檢查日期值：|archivedate= (幫助); 忽略了“2005年”文字 (幫助); 忽略了未知引數|accesdate= (|access-date= 建議) (幫助)

[2] "關於整數長除法（及其變體）的權威高等數學指南". 數學保險庫. 存檔於原始檔案，於 2021年5月14日。 {{cite web}}: 忽略了未知引數|accesdate= (|access-date= 建議) (幫助); 忽略了未知引數|name= (幫助)

[1]

[2]

a