抽象代數/群論/同態

我們終於要進入理論的核心部分了。在本節中，我們將研究群之間的結構保持對映。這項研究將開啟新的途徑，併為我們提供大量的新的定理。

到目前為止，我們一直在“元素級”研究群。由於我們現在即將退一步，在“同態級”研究群，讀者應該預期從本節開始抽象程度會突然增加。我們將嘗試透過始終在這一節中保留一隻腳在“元素級”，來幫助讀者適應這種變化。

從現在開始，符號$e_{G}$將表示群$G$中的單位元，除非另有說明。

群同態

定義 1：令$(G,*)$和$(H,\cdot )$為群。從$G$到$H$的同態是一個函式$\phi \,:\,G\rightarrow H$，使得對於所有$g_{1},g_{2}\in G$，

$\phi (g_{1}*g_{2})=\phi (g_{1})\cdot \phi (g_{2})$.

因此，同態保持群結構。我們在這裡包含了乘法符號，以明確說明左側的乘法發生在$G$中，右側的乘法發生在$H$中。

我們已經看到，本節與之前的章節不同。到目前為止，除了子群之外，我們每次都只處理一個群。不再如此了！讓我們首先從推匯出定義的一些基本且直接的結果開始。

定理 2：令$G,H$為群，$\phi \,:\,G\rightarrow H$為同態。則$\phi (e_{G})=e_{H}$。換句話說，單位元對映到單位元。

證明：設$g\in G$。那麼，$\phi (g)=\phi (e_{G}g)=\phi (e_{G})\phi (g)$，這意味著$\phi (e_{G})$是$H$中的單位元，證明了該定理。∎

定理 3：設$G,H$為群，$\phi \,:\,G\rightarrow H$為同態。那麼對於任意$g\in G$，$\phi (g^{-1})=\phi (g)^{-1}$。換句話說，逆元被對映到逆元。

證明：設$g\in G$。那麼$e_{H}=\phi (e_{G})=\phi (gg^{-1})=\phi (g)\phi (g^{-1})$，這意味著$\phi (g^{-1})=\phi (g)^{-1}$，如需證明。∎

定理 4：設$G,G^{\prime }$為群，$\phi \,:\,G\rightarrow G^{\prime }$為同態，並設$H$為$G$的子群。那麼$\phi (H)=\{\phi (h)\mid h\in H\}$是$G^{\prime }$的子群。

證明：設$h_{1},h_{2}\in H$。則$\phi (h_{1}),\phi (h_{2})\in \phi (H)$，且$\phi (h_{1})\phi (h_{2})^{-1}=\phi (h_{1})\phi (h_{2}^{-1})=\phi (h_{1}h_{2}^{-1})$。由於$h_{1}h_{2}^{-1}\in H$，$\phi (h_{1})\phi (h_{2})^{-1}=\phi (h_{1}h_{2}^{-1})\in \phi (H)$，所以$\phi (H)$是$G^{\prime }$的子群。∎

定理 5：設$G,G^{\prime }$為群，$\phi \,:\,G\rightarrow G^{\prime }$為同態，且$H^{\prime }$為$G^{\prime }$的子群。則$\phi ^{-1}(H^{\prime })=\{g\in G\mid \phi (g)\in H^{\prime }\}$是$G$的子群。

證明：設$g_{1},g_{2}\in \phi ^{-1}(H^{\prime })$。則$\phi (g_{1}),\phi (g_{2})\in H^{\prime }$，並且由於$H^{\prime }$是子群，$\phi (g_{1})\phi (g_{2})^{-1}=\phi (g_{1})\phi (g_{2}^{-1})=\phi (g_{1}g_{2}^{-1})\in H^{\prime }$。但是，$g_{1}g_{2}^{-1}\in \phi ^{-1}(H^{\prime })$，因此$\phi ^{-1}(H^{\prime })$是$G$的子群。∎

從定理4和定理5可以看出，同態保持子群。因此，我們可以期望透過找到合適的同態到$G$來了解群$G$的子群結構。

特別是，每個同態$\phi \,:\,G\rightarrow G^{\prime }$都與兩個重要的子群相關聯。

定義 6：如果同態是雙射的，並且其逆也是一個同態，則稱該同態為同構。如果兩個群之間存在同構，則稱這兩個群為同構，我們用$G\approx H$表示“$G$與$H$同構”。

定理 7：雙射同態是同構。

證明：設$G,H$是群，並設$\phi \,:\,G\rightarrow H$是一個雙射同態。我們必須證明其逆$\phi ^{-1}$也是一個同態。設$h_{1},h_{2}\in H$。那麼存在唯一的$g_{1},g_{2}\in G$使得$\phi (g_{1})=h_{1}$ 以及 $\phi (g_{2})=h_{2}$。那麼我們有$\phi (g_{1}g_{2})=h_{1}h_{2}$，因為$\phi$是一個同態。現在將$\phi ^{-1}$應用於所有等式。我們得到$\phi ^{-1}(h_{1})=g_{1}$，$\phi ^{-1}(h_{2})=g_{2}$ 以及 $\phi ^{-1}(h_{1}h_{2})=g_{1}g_{2}=\phi ^{-1}(h_{1})\phi ^{-1}(h_{2})$，因此$\phi ^{-1}$是一個同態，從而$\phi$是一個同構。∎

定義 8：設$G,G^{\prime }$是群。一個同態，它將$G$中的每個元素都對映到$e^{\prime }\in G^{\prime }$，稱為平凡同態（或零同態），記為$0_{GG^{\prime }}\,:\,G\rightarrow G^{\prime }$

定義 9：設$H$是群$G$的一個子群。則由$i(h)=h$給出的同態$i\,:\,H\rightarrow G$稱為$H$到$G$的包含對映。設$G^{\prime }$是一個與群$G$的一個子群$H$同構的群。則由$i^{\prime }(g^{\prime })=\phi (g^{\prime })$給出的同構$\phi \,:\,G^{\prime }\rightarrow H$誘導了一個單射同態$i^{\prime }\,:\,G^{\prime }\rightarrow G$，稱為$G^{\prime }$到$G$的嵌入。顯然，$i^{\prime }=i\circ \phi$。

定義 10：設$G,G^{\prime }$ 為群，且$\phi \,:\,G\rightarrow G^{\prime }$ 為同態。那麼我們定義以下子群

i) $\ker \,\phi =\{g\in G\mid \phi (g)=e^{\prime }\}\leq G$，稱為$\phi$的核，以及

ii) $\mathrm {im} \,\phi =\{g^{\prime }\in G^{\prime }\mid (\exists g\in G)\phi (g)=g^{\prime }\}\leq G^{\prime }$，稱為$\phi$的像。

定理 11：同態的複合是同態。

證明：設$G,H,K$ 為群，且$\phi \,:\,G\rightarrow H$ 和$\psi \,:\,H\rightarrow K$ 為同態。那麼$\psi \circ \phi \,:\,G\rightarrow K$ 是一個函式。我們必須證明它是一個同態。設$g,h\in G$。那麼$\psi \circ \phi (gh)=\psi (\phi (gh))=\psi (\phi (g)\phi (h))=\psi (\phi (g))\psi (\phi (h))=\psi \circ \phi (g)\psi \circ \phi (h)$，因此$\psi \circ \phi$ 確實是一個同態。 ∎

定理 12：同態的複合是結合的。

證明：這很明顯，因為同態是函式，而函式的複合是結合的。 ∎

推論 13：同構的複合是同構。

證明：這根據定理 11 和雙射的複合是雙射而顯而易見。 ∎

定理 14：設$G,H$ 為群，且$\phi \,:\,G\rightarrow H$ 為一個同態。則$\phi$ 是單射當且僅當$\ker \,\phi =\{e\}\subseteq G$。

證明：假設$\ker \,\phi =\{e\}$ 且 $g_{1},g_{2}\in G$。則 $\phi (g_{1})=\phi (g_{2})\,\Leftrightarrow \phi (g_{1})\phi (g_{2})^{-1}=\phi (g_{1}g_{2}^{-1})=e_{H}$，這意味著 $g_{1}g_{2}^{-1}\in \ker \,\phi$。但根據假設，則 $g_{1}g_{2}^{-1}=e\,\Leftrightarrow g_{1}=g_{2}$，因此 $\phi$ 是單射的。現在假設 $\ker \,\phi \neq \{e\}$ 且 $g\in G$。則存在另一個元素 $k\in \ker \,\phi$，使得 $k\neq e$。但隨後 $\phi (g)=\phi (kg)$。由於 $g$ 和 $kg\neq g$ 都對映到 $\phi (g)=\phi (kg)$，$\phi$ 不是單射的，從而證明了該定理。∎

推論 15：包含對映是單射的。

證明：結果是直接的。由於對於所有$h\in H\leq G$，都有$i(h)=h$，我們有$i^{-1}(e)=\{e\}$。∎

可以看出核滿足一個泛性質。下面的定理解釋了這一點，但對於群的初等處理來說，它異常抽象，如果讀者不能立即理解它，也不要擔心。

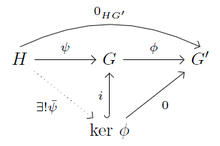顯示核的泛性質的交換圖。

定理 16：設$G,G^{\prime }$是群，$\phi \,:\,G\rightarrow G^{\prime }$是群同態。還設$H$是群，$\psi \,:\,H\rightarrow G$是同態，使得$\phi \circ \psi =0_{HG^{\prime }}$。還設$i\,:\,\ker \,\phi \rightarrow G$是$\ker \,\phi$到$G$的包含對映。則存在唯一的同態${\bar {\psi }}\,:\,H\rightarrow \ker \,\phi$，使得$\psi =i\circ {\bar {\psi }}$。

證明：由於$\phi \circ \psi =0_{HG^{\prime }}$，根據定義，我們必須有$\psi (H)\leq \ker \,\phi$，所以${\bar {\psi }}$ 存在。交換律$\psi =i\circ {\bar {\psi }}$ 然後迫使${\bar {\psi }}(h)=\psi (h)\in \ker \,\phi$，所以${\bar {\psi }}$ 是唯一的。 ∎

定義 17：交換圖是函式網路的一種圖示表示。交換性意味著當從一個物件到同一目標有多條函式複合路徑時，這兩條複合路徑作為函式是相等的。例如，右側的交換圖描述了定理 16 中的情況。在本章關於群的交換圖（或簡稱為圖，我們不會展示不交換的圖）中，所有函式都被隱式地假定為群同態。圖中的單射通常用帶鉤的箭頭強調。此外，滿射通常用雙頭箭頭強調。包含是單射這一點將在稍後證明。

註記 18：從右側的交換圖中，可以完全定義核，而無需引用元素。實際上，定理 16 將成為定義，而我們的定義 10 i) 將成為一個定理。本書不會探討這種思路，但歡迎高階讀者自行推導。

自同構群

在本小節中，我們將研究從一個群到其自身的同態。

定義 19：從一個群$G$到其自身的同態稱為$G$的自同態。既是同態又是同構的自同態稱為自同構。$G$的所有自同態的集合記為$\mathrm {End} (G)$，而$G$的所有自同構的集合記為$\mathrm {Aut} (G)$。

定理 20：$\mathrm {End} (G)$在同態的複合運算下是一個么半群。此外，$\mathrm {Aut} (G)$是一個子么半群，它也是一個群。

證明：我們只需要確認$\mathrm {End} (G)$是封閉的並且具有單位元，我們知道這是正確的。對於$\mathrm {Aut} (G)$，恆等同態$\mathrm {id} _{G}\,:\,G\rightarrow G$是一個同構，並且同構的複合也是同構。因此$\mathrm {Aut} (G)$是一個子么半群。為了證明它是一個群，注意自同構的反自同構也是一個自同構，所以$\mathrm {Aut} (G)$確實是一個群。∎

帶運算子的群

群的自同態可以被認為是該群上的一個一元運算子。這促使了以下定義

定義 21：設$G$是一個群，並且$\Omega \subset \mathrm {End} (G)$。那麼對$(G,\Omega )$稱為帶運算子的群。$\Omega$稱為運算子域，其元素稱為$G$的同態。對於任何$\omega \in \Omega$，我們引入簡寫$\omega (g)=g^{\omega }$，對於所有$g\in G$。因此，$G$的同態是自同態這一事實可以這樣表達：對於所有$a,b\in G$和$\omega \in \Omega$，$(ab)^{\omega }=a^{\omega }b^{\omega }$。

例 22：對於任何群$G$，對$(G,\emptyset )$顯然是一個帶運算子的群。

引理 23：設$(G,\Omega )$是一個帶運算的群。則$\Omega$可以擴充套件到$\mathrm {End} (G)$的一個子么半群$\Omega ^{\prime }$，使得$(G,\Omega ^{\prime })$的結構與$(G,\Omega )$相同。

證明：設$\Omega ^{\prime }$包含恆等自同態，並設$\Omega$是一個生成集。則$\Omega ^{\prime }$在複合運算下是封閉的，是一個么半群。由於$\Omega ^{\prime }$的任何元素都可以表示為$\Omega$中元素的（可能為空的）複合，因此這兩個結構是相同的。∎

在下文中，我們假設運算域始終為么半群。如果不是，我們可以根據引理 23將其擴充套件為么半群。

定義 24：設$(G,\Omega )$和$(H,\Omega )$是具有相同運算域的帶運算的群。則同態$\phi \,:\,(G,\Omega )\rightarrow (H,\Omega )$是一個群同態$\phi \,:\,G\rightarrow H$，使得對於所有$\omega \in \Omega$和$g\in G$，我們有$\phi (g^{\omega })=\phi (g)^{\omega }$。

定義 25：設$(G,\Omega )$ 是一個帶運算的群，$H$ 是 $G$ 的一個子群。則如果對於所有 $h\in H$ 和 $\omega \in \Omega$，都有 $h^{\omega }\in H$，則稱 $H$ 為穩定子群（或$\Omega$-不變子群）。我們說 $H$服從 $G$ 的同態。在這種情況下，$(H,\Omega )$ 是一個帶運算的子群。

例 26：設$V$ 是域 $F$ 上的一個向量空間。如果我們用 $V_{+}$ 表示其在加法下的阿貝爾群，則 $V=(V_{+},F)$ 是一個帶運算的群，其中對於任何 $k\in F$ 和 $v\in V_{+}$，我們定義 $v^{k}=kv$。則穩定子群恰好是 $V$ 的線性子空間（證明這一點）。

習題

問題 1：證明不存在從$\mathbb {Z} _{5}$ 到 $S_{3}$ 的非平凡同態。