高階無機化學/表示

表示

表示是一組矩陣，每個矩陣對應於一個對稱操作，並且以與該群中對稱操作組合相同的方式進行組合。¹ 對稱操作可以用矩陣表示，這讓我們可以透過矩陣計算來理解對稱操作之間的關係。為了理解表示，瞭解對稱操作的矩陣概念至關重要。

以下是一些矩陣形式的對稱操作示例

空間中的一個點 = ${\begin{bmatrix}x\\y\\z\end{bmatrix}}$

E = ${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$

i = ${\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}}$

σ_xy = ${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$

C_n = ${\begin{bmatrix}cos\theta &-sin\theta &0\\sin\theta &cos\theta &0\\0&0&1\end{bmatrix}}$(以z為主要軸)

S_n = ${\begin{bmatrix}cos\theta &-sin\theta &0\\sin\theta &cos\theta &0\\0&0&-1\end{bmatrix}}$(以z為主要軸)

對於C_n操作，θ取決於n，且關係為θ = ${\frac {360}{n}}$。如果對稱性是C₂，那麼θ將是180°，因為分子旋轉了180°。對於C₃，θ將是120°，C₄ θ將是90°，等等。

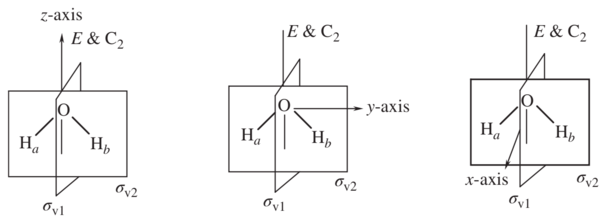
要將對稱操作應用於分子中的原子，可以將矩陣組合起來以產生該群中的另一個操作。對於像圖2中所示的水這樣的C_2v對稱化合物，可以將操作（E、C₂、σ_v1、σ_v2）應用於向量（x、y、z）以找到表示。為了簡化數學運算，可以透過對單個向量進行塊對角化來進行 1x1 矩陣。

例如，

E(y) = [1] [y] = y

C₂(y) = [-1] [y] = -y

σ_v1(y) = σ_xz = [-1] [y] = -y

σ_v2(y) = σ_yz = [1] [y] = y

在這個例子中，如果你將恆等式 (E) 應用於圖3 中所示的向量 y，你將得到 y。如果你將 C₂ 旋轉繞主要軸應用於 y，那麼你將得到 -y，等等。這些獲得的結果顯示了對稱操作後向量的​​位置。對稱操作後每個向量的係數可以用圖1 中所示的字元表中的 Γ_y 表示。這組矩陣，每個矩陣對應於一個矩陣的特徵，就是表示¹。相同的對稱操作可以應用於 x 和 z 以獲得 Γ_x 和 Γ_z 的表示。

圖1. C_2v 中的 xyz 表示。

圖2. 水分子 a) z軸 b) y軸 c) x軸

圖 3. 直角座標系上的 y 向量。

表示可以以與群中對稱運算元組合相同的方式組合，因此，表示每個對稱運算元的矩陣的乘法表也必須以與對稱運算元本身相乘相同的方式相乘。¹ 請參見圖 4。

圖 4. C_2v 點群的乘法表，顯示 1 × 1 矩陣表示如何以與對稱運算元相同的方式相乘。

不可約表示和可約表示

表示可以分為不可約表示和可約表示。字元表中列出了不可約表示，它們是圖 5 中藍色陰影部分。不可約表示有 5 個規則，如下所示。

5 個規則

1. 群的不可約表示的維數的平方和等於群的階。

h =Σ_il_i²

2. 任何不可約表示中字元的平方和等於 h。

h =Σ_i [X_i (R)²]

3. 具有兩個不同不可約表示的字元作為分量的向量是正交的。

Σ_R [X_iR * X_jR] = 0，如果 i =/= j

4. 在給定的表示（可約或不可約）中，屬於同一類對稱運算元的所有矩陣的字元相同。

類直接對應於等效運算的集合。當一個運算可以透過對稱運算可達的新座標系替換另一個運算時，兩個運算屬於同一類。例如，C₇ 點群將具有 C₇¹、C₇²、C₇³、C₇⁴、C₇⁵、C₇⁶、C₇⁷。由於 cos(θ) = cos(θ)，因此與這些矩陣相關的字元相同。在這種情況下，C₇¹=C₇⁶、C₇² = C₇⁵、C₇³ = C₇⁴，以及 C₇⁷ = E，因為它們屬於同一類。我們可以將 C₇ 點群的對稱性簡化為 2 C₇¹、2C₇²、2C₇³ 和 E，因為有兩項操作屬於同一類。

5. 群的不可約表示的數量等於群中類的數量。

圖 5. a) 藍色陰影部分：不可約表示 b) 綠色陰影部分：可約表示 c) 黃色陰影部分：將可約表示簡化為不可約表示

圖 5 中綠色陰影部分是根據對稱運算後未移動的分子數量找到的可約表示。例如，如果我們從圖 5 中檢視 C_2v 對稱分子（例如水）的 Γ_σ，我們將關注對稱運算後未移動的 σ 鍵的數量。在水分子中，有兩個 s 鍵，即兩個 O-H 鍵。如果我們應用 E，兩個鍵都不會移動，因此可約表示將為 2，因為每個未移動的 σ 鍵貢獻 1 個可約表示。如果我們對其應用 C₂ 操作，這兩個鍵都會移動，其中 O-H 鍵會交換位置。這意味著沒有未移動的 σ 鍵，因此可約表示將為零，如圖 5 b 所示。

圖 5 中黃色陰影部分是將可約表示簡化為不可約表示。這可以透過使用公式來完成，n_i = ${1 \over h}$ΣNX_RX_I，其中 n_i = 不可約表示在可約表示中出現的次數，N = 每個對稱元素符號前面的係數（顯示在字元表的頂行），h = 群的階（係數 N 的總和），X_R、X_I = 可約表示和不可約表示的字元。

引用

1.     Pfennig, Brian (2015). 無機化學原理. 新澤西州霍博肯：John Wiley & Sons, Inc.. pp. 195–202. ISBN 978-1-118-85910-0.