工程師與科學家高階數學/尺度分析

尺度分析

在關於無量綱化的章節中，變數（包括自變數和因變數）被無量綱化，同時被縮放，使得它們的值範圍從類似$0$ 到$1$。“類似$0$ 到$1$” 是一種思維方式。

尺度分析是一種利用無量綱化的工具，用於

• 理解一個方程中哪些因素是重要的，更重要的是，哪些因素不重要。
• 在（甚至不）實際求解之前，就能對未知變數的大小有直觀認識，例如速度或溫度。
• 簡化求解過程（無量綱變數範圍在$0$ 到$1$ 之間非常容易處理）。
• 減少解對物理引數的依賴性。
• 允許更高質量的數值解，因為在計算機上，處於同一範圍內的變數能夠更好地保持精度。

尺度分析非常依賴常識，並且沒有太強的系統性。由於這個原因，並且由於它本身就有些非自然且難以在沒有大量例子情況下描述，因此它可能很難學習。

在深入概念之前，我們必須討論數量級。

數量級和大O符號

假設有兩個函式$f(x)$ 和$g(x)$。我們可以說（並用符號表示）

$f(x)\ {\mbox{ is }}\ {\mathcal {O}}(g(x))\ {\mbox{ as }}\ x\to a\ \quad {\mbox{if}}\quad \limsup _{x\to a}\left|{\frac {f(x)}{g(x)}}\right|<\infty \,$

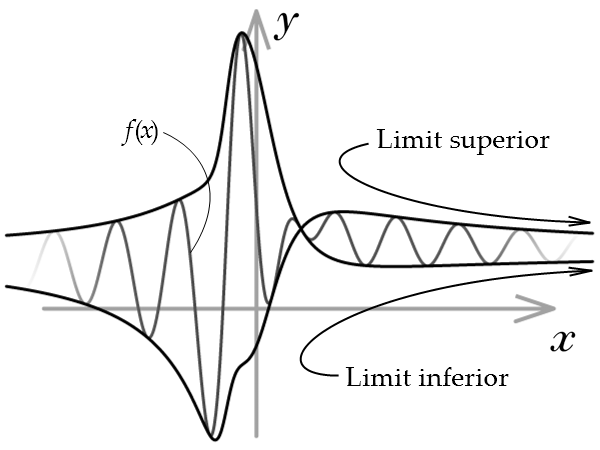當x無限增大時，f(x)的上極限和下極限的視覺化。

值得完全理解這個可能比較模糊的定義。${\mbox{lim sup}}$，即上極限，類似於“普通”極限，只是它是上界的極限。這個概念，以及下極限，在右側進行了說明。這種直觀的分析將不得不在這裡足夠了，因為這些特殊極限的精確定義和細節相當複雜。

作為進一步的例子，當$x$無限增大時，餘弦函式的極限是

$\limsup _{x\to \infty }\ \cos(x)=1\,$

$\liminf _{x\to \infty }\ \cos(x)=-1\,$

$\lim _{x\to \infty }\cos(x)\ {\mbox{ does not exist}}\,$

希望大家能理解這個稍微偏離主題的技術細節，那麼，

$f(x)\ {\mbox{ is }}\ {\mathcal {O}}(g(x))\ {\mbox{ as }}\ x\to a\,$

這個表示式的意思是，在 $x=a$ 附近，$f(x)$ 的 **階**（或者說大小、量級）被 $g(x)$ 限制住了。也就是說，在 $x=a$ 附近，$|f(x)|$ 不會比 $|g(x)|$ 大很多，這正是用極限上確界來表達的原因（普通的極限在這裡行不通，因為振盪會把一切搞砸）。這種涉及大 O 的表示法非常巧妙地被稱為 "大 O 表示法"，它也叫做 Landau 表示法。

例如，考慮 $f(x)=3x^{2}-100x+2$ 在不同點的情況

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(x^{2})\ {\mbox{ as }}\ x\to \infty \,$

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(x^{0})\ {\mbox{ as }}\ x\to 0\,$

在第一種情況下，當 $x$ 很大時，$x^{2}$ 項將輕鬆地佔據主導地位。即使該項的係數非常接近於零，對於足夠大的 x 來說，該項也將佔主導地位。因此，對於很大的 $x$ 來說，該函式的階為 $x^{2}$ 。

在第二種情況下，接近 $x=0$ 時，前兩項趨近於零，而常數項，$2$，根本沒有變化。它被稱為階數為 $1$，記為階數 $x^{0}$。為什麼是 O(1) 而不是 O(2)？兩種說法都正確，但 O(1) 更受歡迎，因為它更簡單，也更接近 $x^{0}$。

這可能會引出一個有趣的問題：如果常數項被刪除會發生什麼？剩下的兩項都會趨近於零。因為我們關注的是 x 接近零而不是等於零，

$3x^{2}-100x\ {\mbox{ is }}\ {\mathcal {O}}(x)\ {\mbox{ as }}\ x\to 0\,$

這是因為隨著 $x$ 趨近於零，二次項比線性項更快地變小。雖然說這個量是 O(1) 也是正確的，但它沒什麼用。說這個量是零階是不正確的，因為無論如何極限都不存在。

如上所述，$g(x)$ 絕不是唯一的函式。以下所有語句都是正確的，僅僅是因為上極限是有界的

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(\sinh(x))\ {\mbox{ as }}\ x\to \infty \,$

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(500\cdot 2^{2^{x}}-\sin(x))\ {\mbox{ as }}\ x\to \infty \,$

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(x)\ {\mbox{ as }}\ x\to 0\,$

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(x^{2})\ {\mbox{ as }}\ x\to 0\,$

雖然從技術上講是正確的，但這些陳述非常誤導人。通常，選擇最簡單、最小幅度的函式 g(x)。

在結束單調之前，還需要提到的是，不需要 $f(x)$ 比 $g(x)$ 在 $x=a$ 附近更小，只需要上極限存在。以下兩個陳述也是正確的

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(0.00001)\ {\mbox{ as }}\ x\to 0\,$

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(1000000000)\ {\mbox{ as }}\ x\to 0\,$

但同樣，這些都是誤導性的，最恰當的說法是

$3x^{2}-100x+2\ {\mbox{ is }}\ {\mathcal {O}}(1)\ {\mbox{ as }}\ x\to 0\,$

一個相對簡單的概念被反覆強調，以至於變得令人困惑。在上下文中會更清晰，並且將在後面的章節中用於不同的目的。

雙項常微分方程的尺度分析

之前，考慮了以下邊值問題

${\frac {d^{2}u}{dy^{2}}}={\frac {P_{x}}{\nu \rho }}\,$

$u(0)=0\,$

$u(D)=0\,$

忘記解決這個簡單問題的任何記憶，本章的概念不關注實際的解。透過定義新的變數對變數進行無量綱化

$u=u_{s}{\hat {u}}\ {\mbox{ , }}\ y=D{\hat {y}}\,$

為了使$y$ 按 $D$ 比例縮放，$u$ 按未知比例 $u_{s}$ 縮放。現在注意到，由於縮放

${\hat {y}}\ {\mbox{ is }}\ {\mathcal {O}}(1)\ {\mbox{, and }}\ {\hat {u}}\ {\mbox{ is }}\ {\mathcal {O}}(1)\,$

這兩個在零附近都是成立的。$u$ 將是 O(1) (讀作“一階”)，當它的尺度被適當選擇時。使用鏈式法則，ODE 被轉化成以下形式

${\frac {u_{s}}{D^{2}}}{\frac {d^{2}{\hat {u}}}{d{\hat {y}}^{2}}}={\frac {P_{x}}{\nu \rho }}\,$

現在，如果 $u$ 和 $y$ 都是一階的，那麼可以假設，至少在感興趣的域的某個點上

${\frac {d^{2}{\hat {u}}}{d{\hat {y}}^{2}}}\ {\mbox{ is }}\ {\mathcal {O}}(1)\,$

當然，這並不能保證是正確的，但它是合理的。

為了識別速度尺度，我們可以將導數等於1 並求解。故意將導數設定為 1 並不會違反任何規則，因為我們只需要某個方程來指定未知常數 $u_{s}$。在定義這個尺度方面有很大的自由度，因為這個常數的值以及如何找到它不會影響 BVP 解的有效性（只要它不是類似 $0$ 的愚蠢值）。

${\frac {u_{s}}{D^{2}}}\cdot 1={\frac {P_{x}}{\nu \rho }}\Rightarrow u_{s}={\frac {D^{2}P_{x}}{\nu \rho }}\,$

由於

${\hat {u}}\ {\mbox{ is }}\ {\mathcal {O}}(1)\,$

因此

$u\ {\mbox{ is }}\ {\mathcal {O}}(u_{s})\Rightarrow u\ {\mbox{ is }}\ {\mathcal {O}}\left({\frac {D^{2}P_{x}}{\nu \rho }}\right)\,}$

可以將此速度尺度視為特徵速度。它是一個數字，告訴我們預期速度的樣子。實際速度可能更大或更小，但這提供了一個大致的概念。此外，此尺度告訴我們更改各種物理引數將如何影響速度；它們中的四個被概括成一個常數。

將此結果與完整解（下劃線）的係數進行比較，其中 u 有量綱，$y$ 無量綱

$u({\hat {y}})={\underline {\frac {D^{2}P_{x}}{2\nu \rho }}}({\hat {y}}^{2}-{\hat {y}})\,$

它們相差一個$2$ 的因子，但它們的大小級相同。因此，確實，$u_{s}$ 表徵速度。

像“合理”和“假設”這樣的詞被使用了幾次，這些詞通常會導致更難聽的詞“近似”。放鬆：BVP 本身並沒有以任何方式被近似或違反。我們只是使用尺度分析來選擇一個速度尺度，該尺度

• 將 ODE 轉化為一個非常容易觀察的東西：${\tfrac {d^{2}{\hat {u}}}{d{\hat {y}}^{2}}}=1\quad ;\quad u(0)=u(1)=0\,$
• 在沒有找到實際解的情況下，很好地瞭解瞭解將產生什麼樣的速度。

請注意，零壓力梯度不再能出現在 ODE 中。這絕不是限制，因為零壓力梯度會導致零速度尺度，這將無條件地導致零速度。

三項偏微分方程的尺度分析

上一節更多的是無量綱化，而不是尺度分析。為了更深入地瞭解這個主題，我們將考慮壓力驅動的瞬態平行板 IBVP，它與上述情況相同，只是有一個時間分量

${\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}-{\frac {P_{x}}{\rho }}\,\,$

$u(0,t)=0\,$

$u(D,t)=0\,$

$u(x,0)=0\,$

請參閱變數變化 章節以回憶此問題的起源。尺度定義如下

$u=u_{s}{\hat {u}}\ {\mbox{ , }}\ y=D{\hat {y}}\ {\mbox{ , }}\ t=t_{s}{\hat {t}}\,$

再次，$y$ 上的刻度是根據邊界條件選擇的，使其成為一階量，而$u$ 和 $t$ 上的刻度只是代表未知量的字母。

鏈式法則已用於根據新變數定義導數。與其採取這種方式，不如回想一下，給定變數$x$ 和 $y$（為了舉例說明）及其各自的刻度$x_{s}$ 和 $y_{s}$

${\frac {\partial ^{n}y}{\partial x^{n}}}={\frac {\partial ^{n}{\hat {y}}}{\partial {\hat {x}}^{n}}}{\frac {y_{s}}{x_{s}^{n}}}\qquad ;\quad x=x_{s}{\hat {x}}\ ,\ y=y_{s}{\hat {y}}\,$

這樣就容易多了。執行變數變換

${\frac {\partial {\hat {u}}}{\partial {\hat {t}}}}{\frac {u_{s}}{t_{s}}}=\nu {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}}{\frac {u_{s}}{D^{2}}}-{\frac {P_{x}}{\rho }}\,\,$

在上一節中，只有一個未知尺度和一個方程，因此可以輕鬆且*唯一地*分離未知尺度。現在，有兩個未知尺度，但只有一個方程（邊界條件/初始條件無濟於事）。該怎麼辦呢？

可以考慮尺度的物理意義。請問：“尺度應該代表什麼？”

**沒有唯一的答案**，但**好的**答案對於這個問題是

• $u_{s}$ 表徵穩態速度。
• $t_{s}$ 表徵響應時間：建立穩態的時間。

再次強調，這些是**選擇的**（但是，對於這個問題，實際上沒有其他選擇）。為了確定尺度，需要考慮每種情況的物理特性。可能沒有唯一的選擇，但有最好的選擇，這些是“正確”的選擇。對偏微分方程中每個項的含義的理解對於識別這些“正確”的選擇至關重要，並在下面進行了說明。

$\underbrace {{\frac {\partial {\hat {u}}}{\partial {\hat {t}}}}{\frac {u_{s}}{t_{s}}}} _{\text{acceleration}}=\underbrace {\nu {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}}{\frac {u_{s}}{D^{2}}}} _{\text{viscosity}}-\underbrace {\frac {P_{x}}{\rho }} _{\begin{smallmatrix}{\text{driving}}\\{\text{force}}\end{smallmatrix}}\,$

對於速度尺度，需要一個穩態條件。在這種情況下，時間導數（加速度）必須很小。我們可以透過要求加速度為某個小值（即零）來獲得與穩態條件相關的特徵速度，並說明二階導數為$O(1)$，並求解

$0={\frac {u_{s}}{D^{2}}}\cdot 1-{\frac {P_{x}}{\nu \rho }}\Rightarrow u_{s}={\frac {D^{2}P_{x}}{\nu \rho }}\,$

這與上一節中找到的速度尺度相同。這是預期的，因為兩種情況都在描述相同的穩態條件。加速度的忽略等同於所謂的驅動力和粘度之間的平衡，因為驅動力和粘度是唯一剩下的因素。

獲得時間尺度可能更加難以捉摸。與達到穩態相關的時間由加速度和粘度決定，因此時間尺度可以透過考慮加速度和粘度之間的平衡來獲得。請注意，此語句與壓力無關，因此它應該適用於各種擾動。為了平衡這些項，假設導數是$O(1)$量，並忽略壓力

$1\cdot {\frac {u_{s}}{t_{s}}}=\nu \cdot 1\cdot {\frac {u_{s}}{D^{2}}}+0\Rightarrow t_{s}={\frac {D^{2}}{\nu }}\,$

這說明

• 粘度越小，達到穩態所需的時間越長。
• 分離距離越小，達到穩態所需的時間越短。

因此，該尺度描述了影響瞬態時間的方式。結果可能看起來違反直覺，但如果壓力確實是一個能夠抵抗高粘度流體可能出現的巨大粘度力的常數，則實驗可以驗證這些結果。

將這些尺度與完整、帶量綱的解中看到的常數進行比較

$u(y,t)={\frac {D^{2}P_{x}}{2\rho \nu }}\left({\frac {y^{2}}{D^{2}}}-{\frac {y}{D}}-\sum _{n=1}^{\infty }e^{-{\frac {\nu (n\pi )^{2}}{D^{2}}}\cdot t}\cdot {\frac {4(-1)^{n}-4}{n^{3}\pi ^{3}}}\sin({\frac {n\pi }{D}}y)\right)\,$

速度尺度在數量級上匹配，這裡沒有新的發現。但仔細檢查時間常數（從指數因子中提取）並與時間尺度進行比較

${\mbox{time constant}}={\frac {D^{2}}{\nu (n\pi )^{2}}}\quad ;\quad t_{s}={\frac {D^{2}}{\nu }}\,$

它們在物理引數方面是同階的，儘管當$n=1$時，它們會相差近10倍。這個結果比看起來更有用。請注意，在確定速度尺度後，方程的所有三個項都可能被考慮以隔離時間尺度。這將是一個糟糕的選擇，因為它不符合上述時間常數，因為它不描述粘度和加速度之間的必要穩定。

假設，對於某個問題，一個時間相關的偏微分方程太難求解，但穩態版本更容易，也是你感興趣的。一個自然的問題是：“我需要等待多長時間才能達到穩態？”

適當尺度分析提供的時間尺度至少會提供一個概念。在這種情況下，假設解中求和的第一個項占主導地位，時間尺度將高估響應時間近10倍，如果你對此一無所知，這是一個寶貴的資訊。這種高估實際上是一個好的（安全的）高估，等待更長時間並確保穩態條件總是更好的。尺度通常具有高估的趨勢。

在結束本節之前，考慮偏微分方程的實際無量綱化。在尺度分析過程中，後兩項的係數相等，之後前兩項的係數相等。這意味著無量綱化的偏微分方程將是

${\frac {\partial {\hat {u}}}{\partial {\hat {t}}}}={\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}}-1\,\,$

這可以透過將為尺度找到的表示式代入偏微分方程來驗證。這個無量綱偏微分方程也證明完全獨立於所涉及的物理引數，這非常方便。

薄壁的熱量傳遞

現在，將介紹尺度分析的一個重要用途：確定方程中什麼重要，更重要的是，什麼不重要。

如拉普拉斯運算元介紹中所述，均勻固體中的穩態熱流可以在三維空間中用以下公式描述：

$\nabla ^{2}=0\qquad {\xrightarrow {\mathrm {It's\ 3D.} }}\qquad {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=0\,$

現在，假設我們對大型且相對薄的牆壁內部的熱量傳遞感興趣，牆壁兩側的溫度不同（不一定均勻）。“薄”這個詞至關重要，現在就把它寫在你的手掌上。你應該懷疑，如果牆壁確實很薄，分析可能會以某種方式簡化，這就是我們接下來要做的。

不關心牆壁邊緣發生的事情，可以寫出邊界值問題：

${\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=0\,$

$u(x,y,0)=f(x,y)\,$

$u(x,y,D)=g(x,y)\,$

$D$是牆壁的厚度（含義：$z$是穿過牆壁的座標）。假設牆壁是一個長方體，尺寸為$s\times s\times D$。使用長方體尺寸作為尺度，

$x=s{\hat {x}}\ ,\quad y=s{\hat {y}}\ ,\quad z=D{\hat {z}}\ ,\quad u=u_{s}{\hat {u}}\,$

只有 $u$ 的比例未知。將其代入 PDE，

${\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {x}}^{2}}}{\frac {u_{s}}{s^{2}}}+{\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}}{\frac {u_{s}}{s^{2}}}+{\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}}{\frac {u_{s}}{D^{2}}}=0\,$

$\left({\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {x}}^{2}}}+{\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}}\right)\left({\frac {D}{s}}\right)^{2}+{\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}}=0\,$

注意，$u$ 的比例被消掉了——因此必須對其比例做出合理的選取；在這種情況下，它將是極端邊界值（例如，$\mathrm {max} (f,g)$ 的最大值），假設它已經被選取並處理了。由於這種縮放和隨後的重新排列，我們可以很好地瞭解方程式中每個項的**量級**

${\bigg (}\underbrace {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {x}}^{2}}} _{{\mathcal {O}}(1)}+\underbrace {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}} _{{\mathcal {O}}(1)}{\bigg )}\cdot \underbrace {\left({\frac {D}{s}}\right)^{2}} _{?}+\underbrace {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}} _{{\mathcal {O}}(1)}=0\,$

每個導數近似為 $O(1)$。但是維度平方比呢？這被稱為無量綱引數。現在看看你的手掌（不是你用來寫字的那隻），回憶“薄”這個詞。“薄”在這個情況下與

${\frac {D}{s}}\ll 1\,$

如果上面的比率遠小於 $1$，那麼這個比率的平方就更小了。我們的無量綱引數被稱為小引數。當引數很小時，有許多機會簡化分析；最簡單的方法是說它太小以至於無關緊要，所以

${\bigg (}\underbrace {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {x}}^{2}}} _{{\mathcal {O}}(1)}+\underbrace {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {y}}^{2}}} _{{\mathcal {O}}(1)}{\bigg )}\cdot \underbrace {\left({\frac {D}{s}}\right)^{2}} _{\begin{smallmatrix}{\text{really}}\\{\text{small}}\end{smallmatrix}}+\underbrace {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}} _{{\mathcal {O}}(1)}=0\quad \Rightarrow \quad {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}}=0\,$

如果沒有對變數進行縮放，使其導數（可能）為 $O(1)$，就無法證明剛才所做的事情，因為你不知道它們的階數。我們知道每個導數都希望是 $O(1)$，但是這些 $O(1)$ 導數中的一些帶有非常小的因子。只有這樣才能合理地丟棄項。無量綱的 BVP 變為

${\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}}=0\,$

${\hat {u}}(s{\hat {x}},s{\hat {y}},0)={\hat {f}}(s{\hat {x}},s{\hat {y}})\,$

${\hat {u}}(s{\hat {x}},s{\hat {y}},1)={\hat {g}}(s{\hat {x}},s{\hat {y}})\,$

需要注意，它仍然是一個偏微分方程（$x$ 和 $y$ 變數並未變得無關緊要 - 請注意邊界條件）。 另外需要注意的是，$u$ 的縮放被取消，因為它無論如何都會抵消（比例仍然可以被選為，比如，最大邊界值）。這個問題可以透過對 $z$ 進行兩次積分來非常簡單地解決，然後考慮邊界條件。

$\int {\frac {\partial ^{2}{\hat {u}}}{\partial {\hat {z}}^{2}}}\ d{\hat {z}}=0\,$

$\int {\frac {\partial {\hat {u}}}{\partial {\hat {z}}}}\ d{\hat {z}}=C_{1}(s{\hat {x}},s{\hat {y}})\,$

${\hat {u}}(x,y,z)=zC_{1}(s{\hat {x}},s{\hat {y}})+C_{2}(s{\hat {x}},s{\hat {y}})\,$

$C_{1}$ 和 $C_{2}$ 是積分“常數”。 第一個邊界條件給出

${\hat {u}}(x,y,0)={\hat {f}}(s{\hat {x}},s{\hat {y}})\,$

$0\cdot C_{1}(s{\hat {x}},s{\hat {y}})+C_{2}(s{\hat {x}},s{\hat {y}})={\hat {f}}(s{\hat {x}},s{\hat {y}})\quad \Rightarrow C_{2}(s{\hat {x}},s{\hat {y}})={\hat {f}}(s{\hat {x}},s{\hat {y}})\,$

第二個是

${\hat {u}}(x,y,1)={\hat {g}}(s{\hat {x}},s{\hat {y}})\,$

$1\cdot C_{1}(s{\hat {x}},s{\hat {y}})+{\hat {f}}(s{\hat {x}},s{\hat {y}})={\hat {g}}(s{\hat {x}},s{\hat {y}})\quad \Rightarrow C_{1}(s{\hat {x}},s{\hat {y}})={\hat {g}}(s{\hat {x}},s{\hat {y}})-{\hat {f}}(s{\hat {x}},s{\hat {y}})\,$

解為

${\hat {u}}(x,y,z)=z\cdot ({\hat {g}}(s{\hat {x}},s{\hat {y}})-{\hat {f}}(s{\hat {x}},s{\hat {y}}))+{\hat {f}}(s{\hat {x}},s{\hat {y}})\,$

這只是說溫度從一個壁面到另一個壁面呈線性變化。值得注意的是，在實踐中，一旦縮放完成，變數上的“帽子”就會被“去掉”，以保持簡潔並防止腕管綜合徵。

注意事項

一維流動近似的失效。

更適合用“極度謹慎”來形容。

在牆壁熱傳遞問題中，我們對 $x$ 和 $y$ 求偏導數為 $O(1)$，這是由縮放比例證明的：${\hat {x}}$，${\hat {y}}$ 和 ${\hat {u}}$ 為 $O(1)$，所以導數也必須如此，對嗎？

不盡然。它們是 $O(1)$ 只是一個線性近似，但是如果函式 $u(x,y,z)$ 對感興趣的變數具有顯著的非線性，那麼導數可能不像預期的那樣是 $O(1)$。在這個問題中，這種情況發生的一種方式是，如果每個牆壁表面的溫度（函式 $f(x,y)$ 和 $g(x,y)$）具有較大且不同的拉普拉斯運算元。這將導致三維熱傳導。

仔細觀察右邊的影像。假設邊長是牆厚的十倍；$f(x,y)$ 和 $g(x,y)$ 在除溫度突然變化的圓圈之外的任何地方都具有零拉普拉斯運算元。在這些位置，拉普拉斯運算元可以很大（如果突然變化是不連續的，則拉普拉斯運算元將是無界的）。這表明所討論的導數不是 O(1)，而是更大，因此即使在這種情況下，這些項也變得重要

${\frac {D}{s}}=0.1\Rightarrow \left({\frac {D}{s}}\right)^{2}=0.01\ll 1\,$

這是由尺度分析所要求的：牆壁顯然很薄。但顯然，小的薄度比乘以大的導數會導致顯著的量。

精確解和透過尺度分析近似得到的解都顯示在切割面的位置。精確解顯示至少二維熱傳遞，而簡化解的解僅顯示一維熱傳遞，並且與精確解有很大差異。

即使不知道拉普拉斯運算元是什麼，也很容易看出為什麼一維近似失敗：這是一個涉及溫度擴散的熱傳遞問題，溫度顯然需要沿著 $x$ 在牆壁內的突然變化附近擴散（不能對邊界條件說同樣的話，因為它們是固定的）。

圖形的標題以“失敗”一詞開頭。這真的是失敗嗎？這取決於你在尋找什麼，可能是也可能不是。請注意，如果牆壁更薄，突然跳躍不是不連續的，那麼精確解和一維解最終可能會再次變得不可區分。