演算法/動態規劃

頂部，章節：1，2，3，4，5，6，7，8，9，A

動態規劃 可以被認為是一種針對特定回溯演算法的最佳化技術，這些回溯演算法會反覆地解決子問題。注意，動態規劃中的“動態”一詞不應該與動態程式語言混淆，比如 Scheme 或 Lisp。“程式設計”一詞也不應該與編寫計算機程式的行為混淆。在演算法的語境中，動態規劃總是指用從其他表格值計算出的值來填充表格的技術。（它之所以是動態的，是因為表格中的值是根據表格的其他值由演算法填充的；它之所以是程式設計，是指在表格中設定值，就像電視節目安排關注的是何時播放什麼節目一樣。）

斐波那契數列

在介紹動態規劃技術之前，先展示一個相關的技術，稱為記憶化，以一個玩具例子來說明：斐波那契數列。我們想要的是一個計算第n個斐波那契數的程式。

// fib -- compute Fibonacci(n)
function fib(integer n): integer

根據定義，第n個斐波那契數，表示為 ${\textrm {F}}_{n}$ 是

{\textrm {F}}_{0}=0

{\textrm {F}}_{1}=1

{\textrm {F}}_{n}={\textrm {F}}_{n-1}+{\textrm {F}}_{n-2}

如何建立一個用於查詢第 n 個斐波那契數的好演算法？讓我們從一個樸素的演算法開始，它對數學定義進行編碼。

// fib -- compute Fibonacci(n)
function fib(integer n): integer
  assert (n >= 0)
  if n == 0: return 0 fi
  if n == 1: return 1 fi
  
  return fib(n - 1) + fib(n - 2)
end

這個程式碼示例也在 Ada 中提供。

注意，這是一個玩具例子，因為已經存在一個關於 ${\textrm {F}}_{n}$ 的數學閉式解。

F(n)={\phi ^{n}-(1-\phi )^{n} \over {\sqrt {5}}}

其中

\phi ={1+{\sqrt {5}} \over 2}

此後一個等式被稱為黃金分割。因此，一個程式可以有效地計算出 ${\textrm {F}}_{n}$ 即使對於非常大的n。但是，瞭解當前演算法的低效之處是很有啟發性的。

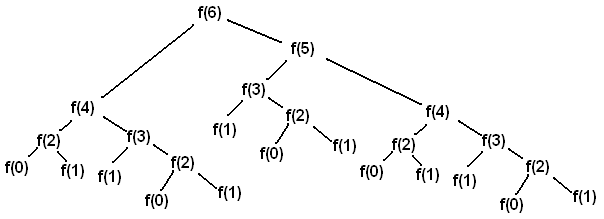
為了分析fib 的執行時間，我們應該看看一個甚至像第 6 個斐波那契數一樣小的數字的呼叫樹。

呼叫樹的每個葉子都有值 0 或 1，這些值的總和是最終結果。因此，對於任何n，呼叫樹中的葉子數實際上等於 ${\textrm {F}}_{n}$ 本身！閉式解因此告訴我們 fib(n) 中的葉子數近似等於

\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}\approx 1.618^{n}=2^{\lg(1.618^{n})}=2^{n\lg(1.618)}\approx 2^{0.69n}.

(注意上面使用的代數運算，將指數的底數改為 2。)這意味著葉子數量過多，特別是考慮到上面呼叫樹中重複出現的模式。

我們可以進行的一種最佳化是，在計算出結果後將其儲存到表中，這樣同一結果只需計算一次。最佳化過程稱為記憶化，並符合以下方法

記憶化方法

從回溯演算法開始
在表中查詢問題；如果存在有效條目，則返回該值
否則，遞迴計算問題，然後在返回該值之前將結果儲存在表中

考慮回溯章節中針對最長公共子序列問題的解決方案。在該演算法的執行過程中，許多公共子問題被重複計算。作為最佳化，我們可以計算這些子問題一次，然後儲存結果以供以後讀取。遞迴記憶化演算法可以“自下而上”地轉換為迭代演算法，該演算法填充子問題的解決方案表。一些解決的子問題在最終結果中可能不需要（這就是動態規劃與記憶化的區別），但動態規劃非常有效，因為迭代版本可以更好地利用快取並減少呼叫開銷。漸近地，動態規劃和記憶化具有相同的複雜度。

那麼，使用記憶化的斐波那契程式如何工作呢？考慮以下程式（f[n] 包含第 n 個斐波那契數，如果已計算，否則為 -1）

function fib(integer n): integer
  if n == 0 or n == 1:
    return n
  else-if f[n] != -1:
    return f[n]
  else
    f[n] = fib(n - 1) + fib(n - 2)
    return f[n]
  fi
end

此程式碼示例也適用於 Ada。

程式碼應該非常清楚。如果 fib(n) 的值已經計算出來，它將儲存在 f[n] 中，然後返回，而不是再次計算。這意味著所有子呼叫樹的副本都從計算中刪除了。

藍色框中的值是已經計算過的值，因此可以跳過呼叫。因此，它比直接的遞迴演算法快得多。由於每個小於 n 的值都計算一次，並且只計算一次，因此在第一次執行時，漸近執行時間為 $O(n)$ 。對它的任何其他呼叫將花費 $O(1)$ ，因為這些值已經預先計算出來了（假設每個後續呼叫的引數都小於 n）。

該演算法確實會消耗大量記憶體。當我們計算 fib(n) 時，fib(0) 到 fib(n) 的值將儲存在主記憶體中。可以改進嗎？是的，可以，儘管後續呼叫的 $O(1)$ 執行時間顯然會丟失，因為這些值不會被儲存。由於 fib(n) 的值僅取決於 fib(n-1) 和 fib(n-2)，我們可以透過自下而上地丟棄其他值。如果我們要計算 fib(n)，我們首先計算 fib(2) = fib(0) + fib(1)。然後，我們可以透過新增 fib(1) 和 fib(2) 來計算 fib(3)。之後，可以丟棄 fib(0) 和 fib(1)，因為我們不再需要它們來計算任何其他值。從 fib(2) 和 fib(3) 我們計算 fib(4) 並丟棄 fib(2)，然後我們計算 fib(5) 並丟棄 fib(3)，等等。程式碼如下

function fib(integer n): integer
  if n == 0 or n == 1:
    return n
  fi

  let u := 0
  let v := 1

  for i := 2 to n:
    let t := u + v
    u := v
    v := t
  repeat
  
  return v
end

此程式碼示例也適用於 Ada。

我們可以修改程式碼以將值儲存在陣列中以供後續呼叫，但重點是我們不需要這樣做。這種方法是動態規劃的典型方法。首先，我們確定要解決哪些子問題才能解決整個問題，然後我們使用迭代過程自下而上地計算這些值。

最長公共子序列（DP 版本）

最長公共子序列 (LCS) 問題涉及比較兩個給定的字元序列，以找到這兩個序列共有的最長子序列。

請注意，“子序列”不是“子串” - 出現在子序列中的字元不必在兩個序列中都是連續的；但是，單個字元確實需要以與兩個序列中出現的順序相同的順序出現。

給定兩個序列，即

X = {x₁, x₂, x₃, ..., x_m} 和 Y = {y₁, y₂, y₃, ..., y_n}

我們定義：

Z = {z₁, z₂, z₃, ..., z_k}

作為 X 的子序列，如果所有字元 z₁, z₂, z₃, ..., z_k 出現在 X 中，並且它們以嚴格遞增的順序出現；即 z₁ 出現在 X 中，先於 z₂，後者又先於 z₃，依此類推。再次強調，所有字元 z₁, z₂, z₃, ..., z_k 不必連續；它們只需要以與 Z 中相同的順序出現在 X 中。因此，我們可以將 Z = {z₁, z₂, z₃, ..., z_k} 定義為 X 和 Y 的公共子序列，如果 Z 同時出現在 X 和 Y 中作為子序列。

LCS 的回溯解決方案涉及列舉 X 的所有可能的子序列，並檢查每個子序列是否也是 Y 的子序列，並跟蹤我們找到的最長子序列 [參見 最長公共子序列（窮舉版本） ]。由於 X 中有 m 個字元，這會導致 2^m 種可能的組合。因此，這種方法需要指數時間，對於長序列來說是不切實際的。

矩陣鏈乘法

假設您需要將一系列 $n$ 個矩陣 $M_{1},\ldots ,M_{n}$ 乘在一起以形成一個乘積矩陣 $P$

P=M_{1}\cdot M_{2}\cdots M_{n-1}\cdot M_{n}

這將需要 $n-1$ 次乘法，但我們以最快的方式形成這個乘積的方法是什麼？矩陣乘法是結合的，即

(A\cdot B)\cdot C=A\cdot (B\cdot C)

對於任何 $A,B,C$ ，因此我們可以選擇先執行哪個乘法運算。(請注意，矩陣乘法不滿足交換律，也就是說，通常情況下 $A\cdot B=B\cdot A$ 不成立。)

因為你一次只能乘以兩個矩陣，所以乘積 $M_{1}\cdot M_{2}\cdot M_{3}\cdot M_{4}$ 可以用以下方式加括號

((M_{1}M_{2})M_{3})M_{4}

(M_{1}(M_{2}M_{3}))M_{4}

M_{1}((M_{2}M_{3})M_{4})

(M_{1}M_{2})(M_{3}M_{4})

M_{1}(M_{2}(M_{3}M_{4}))

兩個矩陣 $M_{1}$ 和 $M_{2}$ 可以相乘，如果 $M_{1}$ 的列數等於 $M_{2}$ 的行數。它們的乘積的行數將等於 $M_{1}$ 的行數，列數將等於 $M_{2}$ 的列數。也就是說，如果 $M_{1}$ 的維度是 $a\times b$ ，而 $M_{2}$ 的維度是 $b\times c$ ，它們的乘積將具有維度 $a\times c$ 。

要將兩個矩陣相乘，我們使用一個名為 matrix-multiply 的函式，該函式接受兩個矩陣並返回它們的乘積。我們暫時不討論這個函式的實現，因為它不是本章的重點（如何以最快的方式將兩個矩陣相乘已經經過多年的深入研究[TODO: 建議將此主題納入高階書籍]）。該函式用於乘以大小為 $a\times b$ 和 $b\times c$ 的兩個矩陣所需要的時間與標量乘法的次數成正比，而標量乘法的次數又與 $abc$ 成正比。因此，括號的放置方式很重要：假設我們有三個矩陣 $M_{1}$ ， $M_{2}$ 和 $M_{3}$ 。 $M_{1}$ 的維度為 $5\times 100$ ， $M_{2}$ 的維度為 $100\times 100$ ，而 $M_{3}$ 的維度為 $100\times 50$ 。讓我們以兩種可能的方式對它們進行括號運算，看看哪種方式需要的乘法次數最少。這兩種方式分別是

((M_{1}M_{2})M_{3})

，以及

(M_{1}(M_{2}M_{3}))

.

第一種方式的乘積需要 75000 次標量乘法（5*100*100=50000 用於形成乘積 $(M_{1}M_{2})$ ，另需 5*100*50=25000 用於最後的乘法）。這看起來可能很多，但與第二種括號方式所需的 525000 次標量乘法（50*100*100=500000 加上 5*50*100=25000）相比，它就微不足道了！你可以看到為什麼確定括號的放置方式很重要：想象一下，如果我們需要乘以 50 個矩陣會發生什麼！

形成遞迴解決方案

請注意，我們專注於找到需要多少次標量乘法，而不是實際的順序。這是因為一旦我們找到一個有效的演算法來找到數量，建立實際括號運算的演算法就很簡單了。不過，我們會在最後進行討論。

那麼，最佳括號運算演算法應該是什麼樣的呢？從章節標題中，你可能會想到使用動態規劃方法（當然不是要給出答案）。那麼，動態規劃方法應該如何工作呢？由於動態規劃演算法是基於最優子結構的，那麼這個問題中的最優子結構是什麼呢？

假設最佳的括號運算方式是

M_{1}M_{2}\dots M_{n}

在 $k$ 處分割乘積

(M_{1}M_{2}\dots M_{k})(M_{k+1}M_{k+2}\dots M_{n})

.

那麼，最優解包含兩個子問題的最優解

(M_{1}\dots M_{k})

(M_{k+1}\dots M_{n})

也就是說，正如動態規劃的基本原理一樣，問題的解依賴於更小子問題的解。

假設用 $c(n)$ 個標量乘法來計算矩陣 $M_{n}$ 和 $M_{n+1}$ 的乘積，而 $f(m,n)$ 是對矩陣 $M_{m}\dots M_{n}$ 進行最優括號化所需的標量乘法次數。 $f(m,n)$ 的定義是邁向解決方案的第一步。

當 $n-m=1$ 時，公式很簡單，就是 $c(m)$ 。但是當距離更大時呢？使用上面的觀察結果，我們可以推匯出一個公式。假設問題的最優解將矩陣在矩陣 k 和 k+1 處分割（即 $(M_{m}\dots M_{k})(M_{k+1}\dots M_{n})$ ），那麼標量乘法次數為。

f(m,k)+f(k+1,n)+c(k)

也就是說，形成第一個產品的所需時間，形成第二個產品的所需時間，以及將它們相乘所需的時間。但是，這個最佳值k是什麼呢？答案當然是使上述公式取最小值的那個值。因此，我們可以形成該函式的完整定義

f(m,n)={\begin{cases}\min _{m\leq k<n}f(m,k)+f(k+1,n)+c(k)&{\mbox{if }}n-m>1\\0&{\mbox{if }}n=m\end{cases}}

對此的直接遞迴解決方案將類似於以下內容 (語言是 Wikicode)

function f(m, n) {

    if m == n
        return 0

    let minCost :=  $\infty$ 

    for k := m to n - 1 {
        v := f(m, k) + f(k + 1, n) + c(k)
        if v < minCost
            minCost := v
    }
    return minCost
}

不幸的是，這種相當簡單的解決方案並不是一個很好的解決方案。它花費大量時間重新計算資料，並且其執行時間呈指數級增長。

要做的
對直接遞迴方法進行分析

要做的
編寫一個記憶版本

使用與上述相同的適應方法，我們得到

function f(m, n) {

    if m == n
        return 0

    else-if f[m,n] != -1:
      return f[m,n]
    fi

    let minCost :=  $\infty$ 

    for k := m to n - 1 {
        v := f(m, k) + f(k + 1, n) + c(k)
        if v < minCost
            minCost := v
    }
    f[m,n]=minCost
    return minCost
}

要做的
編寫一個完整的DP版本

解析任何上下文無關文法

請注意，與這種技術相比，特殊型別的上下文無關文法可以更有效地解析，但在通用性方面，DP方法是唯一可行的。

頂部，章節：1，2，3，4，5，6，7，8，9，A