演算法/爬山法

頂部，章節：1，2，3，4，5，6，7，8，9，A

爬山法是一種用於特定最佳化問題的技術。其思想是從問題的次優解開始（即，從山腳開始），然後重複改進解（爬山），直到某個條件最大化（到達山頂）。

爬山法方法

構建滿足問題約束的次優解
取該解並對其進行改進
重複改進解，直到不再需要/能夠進行改進

最流行的爬山問題之一是網路流問題。儘管網路流聽起來可能有些具體，但它很重要，因為它具有很高的表達能力：例如，實際應用中遇到的許多演算法問題實際上可以被視為網路流的特例。在介紹了爬山方法用於數值問題的簡單示例之後，我們將介紹網路流，然後介紹網路流應用示例。

牛頓求根法

牛頓求根法是一種已有三個世紀的演算法，用於尋找函式根的數值近似值（即，函式f(x) 變為零的點 $x$ ），從初始猜測開始。您需要知道此演算法的函式 $f(x)\,$ 及其一階導數 $f'(x)\,$ 。其思想如下：在初始猜測 $x_{0}$ 的附近，我們可以形成函式的泰勒展開式

f(x)=f(x_{0}+\epsilon )\,

\approx f(x_{0})+\epsilon f'(x_{0})

+{\frac {\epsilon ^{2}}{2}}f''(x_{0})+...

這給出了在 $x_{0}$ 附近對函式的良好逼近。只取右手邊的前兩項，將它們設為零，並解出 $\epsilon$ ，我們得到

\epsilon =-{\frac {f(x_{0})}{f'(x_{0})}}

我們可以用它來構建更好的解決方案

x_{1}=x_{0}+\epsilon =x_{0}-{\frac {f(x_{0})}{f'(x_{0})}}.

這個新的解可以作為再次應用相同過程的起點。因此，一般來說，可以透過反覆應用以下公式來構建更好的近似值

x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.

如插圖所示，這不過是根據初始猜測點的切線構建零點。一般來說，牛頓求根法是二次收斂的，除非解的一階導數 $f'(x)=0\,$ 在根處消失。

回到“爬山”的類比，我們可以將牛頓求根法應用於函式 $f(x)\,$ ，而應用於它的導數 $f'(x)\,$ ，也就是說尋找 $x$ ，使得 $f'(x)=0\,$ 。這將給出函式的極值位置，即它的最大值和最小值。以這種方式從足夠接近最大值的點開始牛頓法，我們就爬上了山。

牛頓法的示例應用

淨現值函式是時間、利率和一系列現金流的函式。一個相關的函式是內部收益率。每期的公式為 (CF_i x (1+ i/100) ^t，這將得到一個多項式函式，即總現金流，當利率等於 IRR 時等於零。在使用牛頓法時，x 是利率，y 是總現金流，該方法將使用多項式的導數函式來找到給定利率（x 值）下圖形的斜率，這將給出 x_n+1，或在下一輪迭代中嘗試找到總回報為零的目標 x 的更好的利率。

除了連續函式，爬山法也可以應用於離散網路。

網路流

假設你有一個有向圖（可能包含迴圈），其中一個頂點標記為源點，另一個頂點標記為目的地或“匯點”。源點只有從它發出的邊，沒有進入它的邊。類似地，目標點只有進入它的邊，沒有從它發出的邊。我們可以假設圖是完全連通的，沒有死衚衕；也就是說，對於每個頂點（除了源點和匯點），至少有一條邊進入該頂點，還有一條邊從該頂點發出。

我們將一個“容量”分配給每條邊，最初我們將只考慮整數值容量。以下圖形滿足我們的要求，其中“s”是源點，“t”是目的地

現在，我們想想象有一系列輸入到達源點，我們希望透過邊將其運送到匯點。我們一次可以傳送到邊上的單位數必須小於或等於邊的容量。你可以將頂點視為城市，將邊視為城市之間的道路，我們希望從源城市儘可能多地將汽車傳送到目的地城市。約束條件是，我們不能沿著一條道路傳送超過其容量的汽車。

網路流的目標是儘可能多地將流量從 $s$ 傳送到 $t$ ，因為每條街道都能承受。

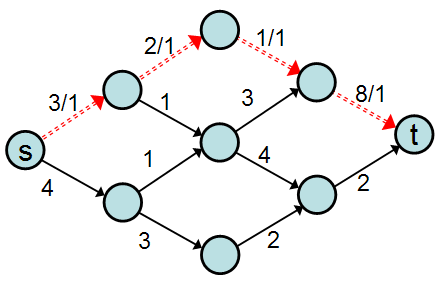
為了組織交通路線，我們可以建立一個從城市 $s$ 到城市 $t$ 的不同路徑的列表。每條路徑的承載能力等於路徑上任意一條邊的最小容量值；例如，考慮以下路徑 $p$

即使 $p$ 的最後一條邊的容量為 8，但該邊上只有一輛車行駛，因為它前面的邊的容量只有 1（因此，該邊已滿負荷）。使用這條路徑後，我們可以透過從每條邊的容量中減去 1 來計算殘差圖

(我們從每個邊在 $p$ 中的容量中減去了 1，因為 1 是 $p$ 的承載能力。）我們可以說路徑 $p$ 的流量為 1。正式來說，流量是將值分配給圖中邊集合的賦值 $f(e)$ ，其中圖 $G=(V,E)$ 中的邊集合。

1.

\forall e\in E:f(e)\in \mathbb {R}

2.

\forall (u,v)\in E:f((u,v))=-f((v,u))

3.

\forall u\in V,u\neq s,t:\sum _{v\in V}f(u,v)=0

4.

\forall e\in E:f(e)\leq c(e)

其中 $s$ 是源節點， $t$ 是匯節點， $c(e)\geq 0$ 是邊 $e$ 的容量。我們將流量 $f$ 的值定義為

{\textrm {Value}}(f)=\sum _{v\in V}f((s,v))

網路流的目標是找到一個 $f$ ，使得 ${\textrm {Value}}(f)$ 最大。最大意味著沒有其他滿足約束 1-4 的流量賦值，其值會更高。流量約束可以解釋為交通中的含義

$\forall e\in E:f(e)\in \mathbb {R}$ 。這條規則簡單地定義了流量為從圖中邊到實數的函式。該函式在圖中所有邊上都定義了。你也可以將“函式”視為對映：每條邊可以是陣列的索引，陣列中邊的值就是該邊上流量函式的值。
$\forall (u,v)\in E:f((u,v))=-f((v,u))$ 。這條規則表明，如果從節點 *u* 到節點 *v* 有流量，那麼從 *v* 到 *u* 的流量應視為負值。例如，如果有兩輛車從城市 *u* 流向城市 *v*，那麼負兩輛車就會往另一個方向行駛。同樣地，如果有三輛車從城市 *u* 流向城市 *v*，而有兩輛車從城市 *v* 流向城市 *u*，那麼淨效應與一輛車從城市 *u* 流向城市 *v*，而沒有車從城市 *v* 流向城市 *u* 相同。
$\forall u\in V,u\neq s,t:\sum _{v\in V}f(u,v)=0$ 。這條規則表明，淨流量（除源點和匯點之外）應該是中性的。也就是說，你不會有更多汽車進入一個城市，比你離開那個城市的汽車多。新車只能從源點進來，而汽車只能儲存在匯點。同樣地，從 *s* 流出的任何流量最終都必須流入 *t*。請注意，如果一個城市有三輛車駛入，它可以將兩輛車送到一個城市，而剩餘的一輛車送到另一個城市。此外，一個城市可能會有來自多個來源的車駛入（儘管所有這些最終都來自城市 *s*）。
$\forall e\in E:f(e)\leq c(e)$ .

Ford-Fulkerson 演算法

以下演算法計算給定圖（具有非負容量）的最大流。演算法執行的操作很容易理解，但要證明它會終止並提供最優解並不容易。

function net-flow(graph (V, E), node s, node t, cost c): flow
  initialize f(e) := 0 for all e in E
  loop while not done
    for all e in E:                         // compute residual capacities
      let cf(e) := c(e) - f(e)
    repeat
    
    let Gf := (V, {e : e in E and cf(e) > 0})

    find a path p from s to t in Gf         // e.g., use depth first search
    if no path p exists: signal done

    let path-capacities := map(p, cf)       // a path is a set of edges
    let m := min-val-of(path-capacities)    // smallest residual capacity of p
    for all (u, v) in p:                    // maintain flow constraints
      f((u, v)) := f((u, v)) + m
      f((v, u)) := f((v, u)) - m
    repeat
  repeat
end

待辦事項
解釋演算法的作用，最好使用圖片。解釋其執行時間。證明它是最優的。展示一個最佳化方案，透過“記住”深度優先搜尋來減少演算法的執行時間。

Ford-Fulkerson 演算法使用對廣度優先搜尋的重複呼叫（使用佇列來安排節點的子節點，使其成為當前節點）。廣度優先搜尋將每條路徑的長度加 1，以便第一條到達目的地的路徑（最短路徑）將第一個出隊。這與使用堆疊形成深度優先搜尋形成對比，深度優先搜尋將找到通往目標的 *任何* 路徑，並檢查當前節點的“後代”，但不一定是最短路徑。

在一次搜尋中，將找到從源點到匯點的路徑。在每次新的搜尋開始時，所有節點都被標記為未標記。已訪問的節點被“標記”，如果再次遇到則不再搜尋。最終，所有可達的節點都將在佇列中排隊，並且無法再從佇列的最後一個節點到達任何未標記的節點。
在搜尋過程中，排隊的節點將記錄其發現的“邊”（由當前節點、發現的節點、當前流量以及從第一個節點到第二個節點方向的總容量組成）。
這使得能夠在到達目標節點後，找到從目標節點到起始節點的逆路徑。一旦找到路徑，就會檢查這些邊以找到剩餘容量最小的邊，這將成為沿著這條路徑產生的流量，並且這個數量將從沿著路徑的每條邊的剩餘容量中移除。在剩餘容量最小的“瓶頸”邊處，將無法再以正向方向進行流量，但仍然可以在反向方向進行流量。
這個過程（對通往目標節點的路徑進行廣度優先搜尋，填充到瓶頸邊的剩餘容量），將不斷重複，直到廣度優先搜尋無法找到通往目標節點的路徑（該節點無法到達，因為通往目標節點的所有邊序列的瓶頸邊都已填滿）。因此，先前找到的路徑的副作用的記憶將記錄在邊的流量中，並影響未來搜尋的結果。
最大流的一個重要特性是，流量可以發生在邊的反方向，並且反方向的剩餘容量等於正方向的當前流量。通常，邊正方向的剩餘容量等於初始容量減去正向流量。直觀地說，這使得有更多選擇來最大化流量，因為早期增廣路徑會阻塞較短路徑。
在終止時，演算法將保留最後一次廣度優先搜尋（從起始節點開始，不標記目標節點）結果的標記和未標記狀態。
最小割狀態是由最後一次不成功的廣度優先搜尋（從起始節點開始，不標記目標節點）形成的兩個標記和未標記節點集。起始節點屬於割的一側，而目標節點屬於另一側。任意地，“在割中”意味著在起始節點一側，或者是一個標記節點。請回憶一下，給定一條帶有流量和剩餘容量的邊，節點是如何被標記的。

Ford-Fulkerson 最大流/最小割的示例應用

Ford-Fulkerson 的一個應用示例是棒球賽季淘汰賽。問題是球隊是否可以透過超過其他球隊的總勝場數的某種組合來贏得整個賽季。

這個想法是建立一個流圖，其中球隊不能超過目標球隊在整個賽季中可能獲得的最大總勝場數。有一些比賽節點，其邊代表兩支球隊之間剩餘的比賽次數，每個比賽節點透過不會限制正向流量的邊流出到兩個球隊節點；球隊節點從他們參與的所有比賽接收邊。然後，具有勝場限制容量的流出邊流向虛擬目標節點。在目標節點的總勝場數將超過其他球隊勝場數的某種組合的最大流狀態下，倒數第二次深度優先搜尋將切斷起始節點與圖的其餘部分，因為由於倒數第二次深度優先搜尋（回憶演算法第二部分找到路徑後對流量的影響），無法流向任何比賽節點。這是因為，在尋求每條路徑的最大流時，比賽邊的容量將被路徑上更遠的勝場限制邊最大程度地消耗，而任何剩餘的比賽容量意味著還有更多的比賽要進行，這將使至少一支球隊超過目標球隊的最大勝場數。如果一個球隊節點在最小割中，那麼就有一條通往該球隊的邊具有剩餘容量，這意味著根據前面的陳述，該球隊是什麼？在最小割中找到的球隊集代表什麼（提示：考慮比賽節點邊）？

二分匹配（實習生匹配）最大值示例

這個匹配問題不包括偏好權重。一組公司提供工作，這些工作被歸為一個大集合，而實習生則申請特定公司的特定工作。申請是權重為 1 的邊。為了將二分匹配問題轉換為最大流問題，將建立虛擬頂點 s 和 t，它們從 s 到所有實習生，以及從所有工作到 t 具有權重為 1 的邊。然後使用 Ford-Fulkerson 演算法透過增廣找到的路徑來依次飽和圖中的 1 容量邊。可能會出現這樣的中間狀態：剩餘的實習生和工作都沒有匹配，但是沿著具有剩餘容量 = 正向流量 = 1 的反向邊回溯（沿著後來廣度優先搜尋期間出現的更長路徑）將否定先前次優的增廣路徑，並提供進一步的搜尋選擇以進行匹配，並且僅在達到最大流或最大匹配時終止。

頂端,

章節：1，2，3，4，5，6，7，8，9，A