頂部,章節:1,2,3,4,5,6,7,8,9,A
在我們開始學習演算法技術之前,我們將先繞道介紹一些必要的數學工具。首先,我們將介紹一些將在本書後面使用的術語的數學定義。透過擴充套件你的數學詞彙,你可以更加精確地描述問題或更容易地表達問題。然後,我們將介紹分析演算法執行時間的方法。在本專著中,我們將在介紹每個主要演算法之後給出其執行時間的分析以及其正確性的證明。
除了正確性之外,另一個重要的演算法特徵是其時間和記憶體消耗。時間和記憶體都是寶貴的資源,它們在使用方式上存在顯著差異(即使兩者都充足)。
如何衡量資源消耗?一種方法是建立一個函式,用輸入的一些特徵來描述資源的使用情況。一個常用的輸入資料集特徵是其大小。例如,假設一個演算法以一個包含  個整數的陣列作為輸入。我們可以將這個演算法所需的時間描述為一個以
個整數的陣列作為輸入。我們可以將這個演算法所需的時間描述為一個以  為變數的函式
為變數的函式  。例如,我們可以寫成
。例如,我們可以寫成

其中  是某個時間單位(在本討論中,主要關注的是時間,但我們也可以用它來描述記憶體消耗)。時間單位很少是實際的秒數,因為這會取決於機器本身、它執行的系統以及系統負載。相反,時間單位通常用執行某些基本操作的次數來表示。例如,我們可能關心的一些基本操作包括:所需的加法或乘法次數;元素比較次數;記憶體位置交換次數;或執行的機器指令數量。通常,我們可能會簡單地將這些執行的基本操作稱為執行的步驟。
是某個時間單位(在本討論中,主要關注的是時間,但我們也可以用它來描述記憶體消耗)。時間單位很少是實際的秒數,因為這會取決於機器本身、它執行的系統以及系統負載。相反,時間單位通常用執行某些基本操作的次數來表示。例如,我們可能關心的一些基本操作包括:所需的加法或乘法次數;元素比較次數;記憶體位置交換次數;或執行的機器指令數量。通常,我們可能會簡單地將這些執行的基本操作稱為執行的步驟。
這是否是確定演算法資源消耗的好方法?是也不是。當兩種不同的演算法在時間消耗上相似時,精確的函式可能有助於確定在給定條件下哪個演算法更快。但在許多情況下,計算執行所需操作確切數量的解析描述要麼很困難,要麼根本不可能,尤其是在演算法根據其輸入的值有條件地執行操作時。相反,真正重要的是不是完成函式所需的精確時間,而是資源消耗根據其輸入變化的程度。具體而言,考慮以下兩個函式,它們分別代表每個輸入資料集大小所需的計算時間


它們看起來很不同,但它們的行為如何?讓我們看看函式的一些影像( 為紅色,
為紅色, 為藍色)
為藍色)
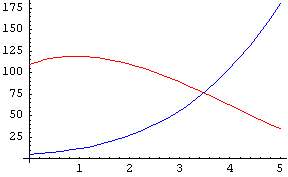 f 和 g 在 0 到 5 範圍內的影像 f 和 g 在 0 到 5 範圍內的影像 |
 f 和 g 在 0 到 15 範圍內的影像 f 和 g 在 0 到 15 範圍內的影像
|
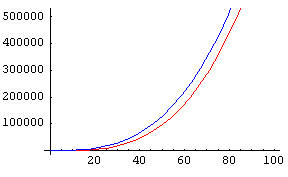 f 和 g 在 0 到 100 範圍內的影像 f 和 g 在 0 到 100 範圍內的影像 |
 f 和 g 在 0 到 1000 範圍內的影像 f 和 g 在 0 到 1000 範圍內的影像
|
在第一個非常有限的影像中,曲線看起來有些不同。在第二個影像中,它們開始以某種方式呈現相同的趨勢,在第三個影像中,它們之間只有很小的差異,最後它們幾乎完全相同。實際上,它們逼近  ,即主導項。當 n 變大時,其他項與 n3 相比變得微不足道。
,即主導項。當 n 變大時,其他項與 n3 相比變得微不足道。
正如你所看到的,修改多項式時間演算法的低階係數並沒有太大幫助。真正重要的是最高階係數。這就是為什麼我們採用了這種符號來進行這種分析。我們說

我們忽略了低階項。我們可以說

這為我們提供了一種更便捷的方式來比較不同的演算法。對 個元素進行插入排序需要
個元素進行插入排序需要 數量級的步驟。歸併排序的排序步驟為
數量級的步驟。歸併排序的排序步驟為 。因此,一旦輸入資料集足夠大,歸併排序就會比插入排序更快。
。因此,一旦輸入資料集足夠大,歸併排序就會比插入排序更快。
一般來說,我們寫

當

也就是說, 成立當且僅當存在一些常數
成立當且僅當存在一些常數 和
和 ,使得對於所有
,使得對於所有 ,
, 為正且小於等於
為正且小於等於 。
。
注意,此符號中使用的等號描述了 和
和 之間的關係,而不是反映真正的相等性。鑑於此,有些人用集合來定義大O符號,指出
之間的關係,而不是反映真正的相等性。鑑於此,有些人用集合來定義大O符號,指出

當

大O符號只是一個上界;這兩個都是真的


如果我們將等號用作等式,我們會得到非常奇怪的結果,例如

這顯然是胡說八道。這就是為什麼集合定義很方便。你可以透過將等號視為單向等式來避免這些情況,即

並不意味著

始終將 O 保持在右側。
有時,我們想要更多地瞭解某個函式行為的上界。大 Omega 提供了下界。一般來說,我們說

當

即  當且僅當存在常數 c 和 n0 使得對於所有 n>n0 f(n) 為正且大於或等於 cg(n)。
當且僅當存在常數 c 和 n0 使得對於所有 n>n0 f(n) 為正且大於或等於 cg(n)。
所以,例如,我們可以說
 ,(c=1/2, n0=4) 或
,(c=1/2, n0=4) 或 ,(c=1, n0=3),
,(c=1, n0=3),
但聲稱

當給定函式同時為 O(g(n)) 和 Ω(g(n)) 時,我們說它是 Θ(g(n)),並且我們對該函式有了嚴格的界限。函式 f(n) 為 Θ(g(n)) 時

但大多數時候,當我們試圖證明給定的  時,我們並不使用這個定義,而是證明它同時是 O(g(n)) 和 Ω(g(n))。
時,我們並不使用這個定義,而是證明它同時是 O(g(n)) 和 Ω(g(n))。
當漸近界限不緊密時,我們可以用  或
或  來表達。定義如下:
來表達。定義如下:
- f(n) 是 o(g(n)) 當且僅當
 ,並且
,並且
- f(n) 是 ω(g(n)) 當且僅當

請注意,當對於 g 的任何係數,g 最終都大於 f 時,函式 f 屬於 o(g(n));而對於 O(g(n)),只需要存在一個係數,使得 g 最終至少與 f 一樣大。
給定兩個引數的函式  和
和  ,
,
 當且僅當
當且僅當  。
。
例如, ,以及
,以及  。
。
合併排序 n 個元素: 這描述了合併排序的一次迭代:問題空間
這描述了合併排序的一次迭代:問題空間  被縮減成兩個一半 (
被縮減成兩個一半 ( ),然後在所有遞迴呼叫結束時合併在一起 (
),然後在所有遞迴呼叫結束時合併在一起 ( )。這個符號系統是演算法分析的精髓,所以要習慣它。
)。這個符號系統是演算法分析的精髓,所以要習慣它。
有一些定理可以用來估計一個函式的 Big Oh 時間,前提是它的遞迴方程符合某種模式。

|
要
寫這部分
|
對你的方程的 Big Oh 時間做一個猜測。然後使用歸納法證明這個猜測是正確的。

|
要
寫這部分
|

|
要
展示常用求和的封閉形式並證明它們
|
這實際上只是一種獲得明智猜測的方法。你仍然必須回到替換法來證明 Big Oh 時間。

|
要
寫這部分
|
考慮一個遞迴方程,它符合以下公式

對於 a ≥ 1, b > 1 和 k ≥ 0。這裡,a 是每次函式呼叫產生的遞迴呼叫次數,n 是輸入大小,b 是每次輸入縮小多少,k 是每次函式呼叫(除了基本情況)執行的操作的多項式階數。例如,在後面介紹的合併排序演算法中,我們有

因為每次非基本情況迭代都會呼叫兩個子問題,並且陣列的大小每次都會減半。最後的  是這個分治演算法的“征服”部分:將兩個遞迴呼叫的結果合併成最終結果需要線性時間。
是這個分治演算法的“征服”部分:將兩個遞迴呼叫的結果合併成最終結果需要線性時間。
將 T 的遞迴呼叫視為形成一棵樹,有三種可能的情況來確定演算法的大部分時間都花在哪裡(這裡“大部分”指的是它的漸進行為)
- 這棵樹可能是頭重腳輕的,大部分時間花在接近根部的初始呼叫上;
- 這棵樹可能有一個穩定狀態,時間均勻分佈;或者
- 這棵樹可能頭輕腳重,大部分時間花在接近葉子的呼叫上
根據樹處於這三種狀態中的哪一種,T 將有不同的複雜度
對於上面提到的歸併排序示例,其中

我們有

因此, ,所以這也處於“穩定狀態”:根據主定理,歸併排序的複雜度因此為
,所以這也處於“穩定狀態”:根據主定理,歸併排序的複雜度因此為
 .
.
(從圖的鄰接表表示開始,並顯示兩個巢狀的for迴圈:一個用於每個節點n,另一個巢狀在該迴圈中,用於每個邊e。如果有n個節點和m個邊,這可能導致你說迴圈需要O(nm)時間。但是,只有在一次迴圈中,內部迴圈才能花費那麼長時間,更緊密的界限是O(n+m)。)
頂部,章節:1,2,3,4,5,6,7,8,9,A




























































