微積分/雙曲函式

理論

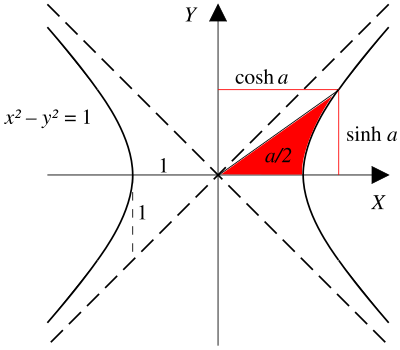
單位雙曲線有一個扇區，其面積為雙曲角的一半

雙曲函式的自變數稱為雙曲角。正如圓函式正弦和餘弦可以看作是單位圓到軸的投影，雙曲函式正弦和餘弦可以看作是單位雙曲線到軸的投影。

定義

雙曲函式的定義類似於三角函式

$\sinh(x)={\frac {e^{x}-e^{-x}}{2}}$

$\cosh(x)={\frac {e^{x}+e^{-x}}{2}}$

$\tanh(x)={\frac {\sinh(x)}{\cosh(x)}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$

從這些函式定義倒數函式csch，sech，coth

${\rm {csch}}(x)={\frac {1}{\sinh(x)}}$

${\rm {sech}}(x)={\frac {1}{\cosh(x)}}$

$\coth(x)={\frac {1}{\tanh(x)}}$

一些簡單的恆等式

$\cosh ^{2}(x)-\sinh ^{2}(x)=1$

$1-\tanh ^{2}(x)={\rm {sech}}^{2}(x)$

$\sinh(2x)=2\sinh(x)\cosh(x)$

$\cosh(2x)=\cosh ^{2}(x)+\sinh ^{2}(x)$

雙曲函式的導數

${\frac {d}{dx}}\sinh(x)=\cosh(x)$

${\frac {d}{dx}}\cosh(x)=\sinh(x)$

${\frac {d}{dx}}\tanh(x)={\rm {sech}}^{2}(x)$

${\frac {d}{dx}}{\rm {csch}}(x)=-{\rm {csch}}(x){\rm {coth}}(x)$

${\frac {d}{dx}}{\rm {sech}}(x)=-{\rm {sech}}(x)\tanh(x)$

${\frac {d}{dx}}{\rm {coth}}(x)=-{\rm {csch}}^{2}(x)$

主要雙曲函式的主值

對於 sinh 和 tanh 定義主支沒有問題，因為它們是單射的。我們為 cosh 選擇其中一個主支。

$\sinh :\mathbb {R} \to \mathbb {R}$

$\cosh :[0,\infty ]\to [1,\infty ]$

$\tanh :\mathbb {R} \to (-1,1)$

反雙曲函式

在上述主值定義下，反函式的定義是直接的

${\rm {arsinh:\mathbb {R} \to \mathbb {R} }}$

${\rm {arcosh:[1,\infty ]\to [0,\infty ]}}$

${\rm {artanh:(-1,1)\to \mathbb {R} }}$

我們可以定義 ${\rm {arcsch}}$ , ${\rm {arsech}}$ 和 ${\rm {arcoth}}$ 類似地。

我們也可以使用對數函式來寫這些反函式，

${\rm {arsinh}}(x)=\ln {\big (}x+{\sqrt {x^{2}+1}}{\big )}$

${\rm {arcosh}}(x)=\ln {\big (}x+{\sqrt {x^{2}-1}}{\big )}$

${\rm {artanh}}(x)=\ln \left({\sqrt {\frac {1+x}{1-x}}}\right)$

這些恆等式可以簡化一些積分。

反雙曲函式的導數

${\frac {d}{dx}}{\rm {arsinh}}(x)={\frac {1}{\sqrt {1+x^{2}}}}$

${\frac {d}{dx}}{\rm {arcosh}}(x)={\frac {1}{\sqrt {x^{2}-1}}}\ ,\ x>1$

${\frac {d}{dx}}{\rm {artanh}}(x)={\frac {1}{1-x^{2}}}\ ,\ |x|<1$

${\frac {d}{dx}}{\rm {arcsch}}(x)=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}\ ,\ x\neq 0$

${\frac {d}{dx}}{\rm {arsech}}(x)=-{\frac {1}{x{\sqrt {1-x^{2}}}}}\ ,\ 0<x<1$

${\frac {d}{dx}}{\rm {arcoth}}(x)={\frac {1}{1-x^{2}}}\ ,\ |x|>1$

超越函式

雙曲函式是超越函式的例子——它們不是代數函式。它們包括三角函式、反三角函式、對數函式和指數函式。